2.2.3. Обучение с масштабированием подобных ситуаций

В процессе обучения и работы обучаемой системы управления могут возникать ситуации, соответствующие признаки которых отличаются друг от друга в одно и то же число раз (для двух образов: b_i2 = k · b_i1). Это возможно, например, при изменении уровня освещенности обозреваемой сцены. Такие ситуации являются подобными, а величина k – отношение подобия этих ситуаций. Обучение формированию сигналов управления исполнительным двигателем, не отвечающих условию: E₂ = k · E₁, для таких ситуаций невозможно. Для преодоления этого ограничения в изображения этих ситуаций можно искусственно ввести дополнительный масштабирующий признак некоторой постоянной величины, например на дополнительный рецептор подавать постоянный сигнал для всех ситуаций. Степень совпадения двух ситуаций S определяется выражением 2.12. Для подобных ситуаций S = 1. Оптимальный масштабирующий признак должен быть таким, чтобы значение степени совпадения для данных двух ситуаций стало минимальным. При использовании масштабирования степень совпадения двух ситуаций будет иметь вид

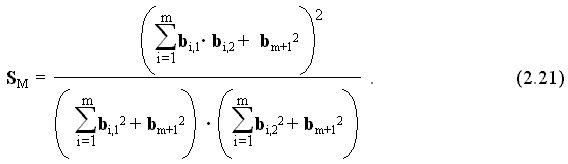
Отсюда следует, что степень совпадения двух ситуаций будет минимальной при

Для двух подобных ситуаций оптимальный масштабирующий признак определится как

Из выражений (2.21) и (2.22) следует, что минимальная степень совпадения двух подобных ситуаций, достигаемая масштабированием, определяется только отношением подобия k и связана с ним зависимостью

S_min = 4 k / (1 + k)² .___________________(2.23)

В качестве примера рассматриваются две ситуации, представленные наборами признаков:

B₁: ___ 2 __ 8 __ 1 __ 5 __ 4 __ 7 __ 3 _ 11 __ 9 __ 6 ; B₂: ___ 6 _ 24 __ 3 _. 15 _ 12 _ 21 __ 9 _ 33 _. 27 _ 18 .

Здесь число признаков: m = 10 , отношение подобия: k = 3 , степень совпадения ситуаций: S = 1 . Оптимальный масштабирующий признак, определенный по формуле (2.22), будет иметь значение b_m+1= 34,899857. Степень совпадения для масштабированных ситуаций

B₁^*: ___ 2 __ 8 __ 1 __ 5 __ 4 __ 7 __ 3 _ 11 __ 9 __ 6 _ 34,899857; B₂^*: ___ 6 _ 24 __ 3 _. 15 _ 12 _. 21 __ 9 _ 33 _ 27 _ 18 _ 34,899857,

в соответствии с формулами (2.21) и (2.23), имеет значение S_M = 0,75 .

Кроме формирования отличительности подобных ситуаций, масштабирование может быть использовано и для сокращения длительности обучения, причем не только для подобных ситуаций. Если обучателю известны значения сигналов управления, соответствующие двум ситуациям, то из анализа зависимостей ошибок сигналов управления от числа циклов обучения (2.15, 2.16) может быть найдено значение масштабирующего признака, обеспечивающего минимальную продолжительность обучения. Так, оптимальный масштабирующий признак, определенный по формуле

или для подобных ситуаций:

позволяет осуществить обучение за один цикл. Для двоичных ситуаций, признаки которых могут принимать только два значения: ноль и единицу, – формула (2.24) примет вид

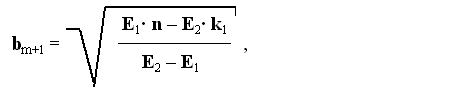
где n – число совпадающих признаков двоичных ситуаций, k₁ – число единичных признаков первой ситуации. Для рассматриваемых ситуаций B₁ и B₂ с соответствующими выходными сигналами E₁ = 1 и E₂ = 2 оптимальный масштабирующий признак, определенный по формуле (2.25), будет иметь значение: b_m+1 = 20,149442. На рис.2.2 показана зависимость степени отличия D рассматриваемых ситуаций и числа циклов обучения t от величины масштабирующего признака b_m+1 при заданной точности выходных сигналов  _E =  0,1.

1 – график зависимости t = f(b_m+1) для ситуаций с признаками B₁ и B₂ при E₁ = 1 , E₂ = 2; 2 – график зависимости t = f(b_m+1) для ситуаций с признаками B₁ и B₂ при E₁ = 2 , E₂ = 1 Рис.2.2. Зависимость продолжительности обучения от значения масштабирующего признака для подобных образов

Следует отметить, что масштабирование обеспечивает сходимость процесса обучения для любых двух подобных ситуаций.