20 Похідні та диференціали вищих порядків. Формула Лейбніца.
Нехай
функція
диференційовна
на проміжку X,
а
її похідна, яка також є функцією відносно
x.
Від цієї функції знову можна шукати
похідну за умови, що вона існує на
заданому проміжку. Похідна від похідної
називається
похідною
другого порядку
функції
і
позначається одним із символів:
.
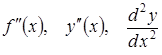Так
у фізиці, якщо
закон, за яким змінюється пройдений
шлях при прямолінійному русі точки, то
є
прискоренням
цієї точки в момент часу t.
Аналогічно
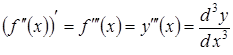і
т. д.
Взагалі
похідною
n-го
порядку
від функції
називається
похідна від похідної
-го
порядку і позначається
,
або
,
або
.
Зауваження.
При
,
похідну n-го
порядку позначають відповідно
;
при
позначають:
або
.
Приклад 3.17. Знайти похідну другого порядку від функції
.
Розв’язання.
Знаходимо спочатку
за
формулою
.
.
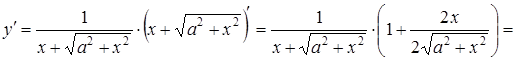
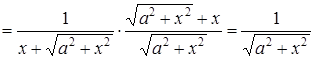Знаходимо похідну від отриманої функції:
,
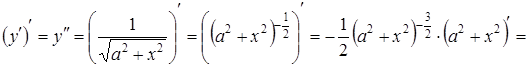
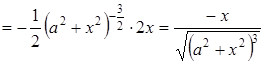тобто
.
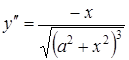Формула
Лейбніца.
Якщо функції
,
мають
похідні до n-го
порядку включно, то для обчислення
похідної n-го
порядку від добутку цих функцій
використовують формулу Лейбніца:
.
(3.14)
Похідні вищих порядків від функцій, заданих параметрично.
Якщо
функції
і
параметрично
задають функцію
,
то похідні
,
,
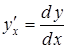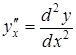можна послідовно обчислити за формулами:
,
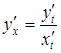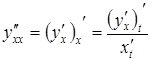і
т. д.
Так, для похідної другого порядку має місце формула:
.
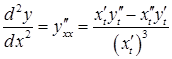(3.15)
Диференціали вищих порядків. Нехай функція диференційовна на проміжку X. Її диференціал
називається
також диференціалом
першого порядку
і його можна розглядати як функцію
змінної x
(приріст аргументу
вважається
сталим).
Означення
3.4.
Диференціалом
другого
порядку
(second
differential)
функції
в
точці x
називається диференціал від її
диференціала першого порядку (за умови,
що повторний приріст незалежної змінної
x
збігається з попереднім
)
і позначається
:
.
За означенням маємо
,
позначають
.
Таким чином
.
(3.16)
Аналогічно,
диференціалом
n-го
порядку
(позначається
),
n=2,3,...
називається диференціал від диференціала
порядку
за
умови, що в диференціалах весь час
беруться одні й ті самі прирости
незалежної
змінної x.
Тобто
.
При цьому справедлива формула:
.
(3.17
Формула Ньютона-Лейбница
Формула Ньютона-Лейбница относится к математическому анализу и является основной формулой интегрального исчисления! Ранее, когда мы рассматривали Формулу бинома Ньютона, мы сказали что Исааку Ньютону принадлежит роль "Отца современной математики". Ньютон вместе с Лейбницем, Огюстеном Коши, Кантором, Леонардом Эйлером и другими заложили основы современного дифференциального и интегрального исчисления, хотя строгое и стройное построение математического анализа возникло несколько позже. Благодаря формуле Ньютона-Лейбница устанавливается связь между определенным и неопределенным интегралом. А именно: Чтобы решить определенный интеграл, надо сначала вычислить неопределенный интеграл (или найти первообразную), а затем вычислить определенный интеграл, подставив первообразную подынтегральной функции в формулу Ньютона-Лейбница:
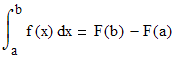
Здесь F(x) - первообразная для функции f(x)! Таким образом, чтобы применить формулу Ньютона-Лейбница, надо вычислить значение первообразной при верхнем пределе интегрирования B, при нижнем пределе интегрирования - A, а затем взять их разность F(b)-F(a). Вначале мы рассмотрим доказательство данной формулы, а затем приведем Примеры решения интегралов по основной формуле интегрального и дифференциального исчисления.