
- •Операционное исчисление
- •22.1. Оригинал. Изображение
- •Задание
- •22.2. Простейшие свойства преобразования лапласа
- •4. Дифференцирование оригинала
- •5. Интегрирование оригинала
- •6. Дифференцирование изображения
- •7. Интегрирование изображения
- •Теоремы о сдвиге аргументов оригинала и изображения
- •22.4. Изображение периодического сигнала
- •22.5. Восстановление оригинала
- •22.6. Обращение преобразования лапласа
- •22.7. Примеры применения операционного исчисления к решению дифференциальных уравнений и систем дифференциальных уравнений с постоянными коэффициентами
- •22.8. Свертка односторонних функций; ее свойства. Теорема бореля*
- •22.9. Формулы дюамеля. Применение их к решению дифференциальных уравнений
5. Интегрирование оригинала
Если
– оригинал и
,
,
то функция
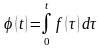 также является оригиналом, причем
также является оригиналом, причем
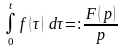 ,
, (10)
,
, (10)
т.е. интегрированию оригинала соответствует деление изображения на .
В самом деле, функция удовлетворяет определению оригинала:
1) по свойству определенного интеграла с переменным пределом функция либо непрерывна всюду, либо имеет конечное число точек разрыва первого рода на произвольном отрезке конечной длины;
2)
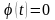 при
при
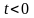 ,
так как
,
так как
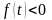 при
,
причем
при
,
причем
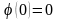 ;
;
3)
для
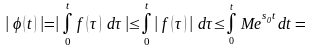
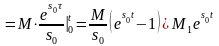 ,
здесь использованы свойства оригинала
,
– показатель роста функций
и
.
,
здесь использованы свойства оригинала
,
– показатель роста функций
и
.
Обозначим
изображение функции
через
.
По свойству интеграла с переменным
верхним пределом
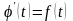 и
и
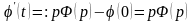 (см. формулу (7)). Из равенства
(см. формулу (7)). Из равенства
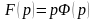 устанавливаем (10).
устанавливаем (10).
ПРИМЕР
9. Применить формулу
(10) к степенным функциям
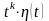 ,
,
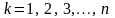 .
.
Решение.
Представим
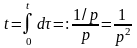 ,
получим соотношение
,
получим соотношение
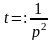 ,
аналогично
,
аналогично
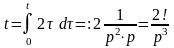 ,
т.е.
,
т.е.
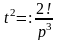 .
В общем случае
.
В общем случае
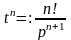 .
.
6. Дифференцирование изображения
Дифференцированию
изображения соответствует умножение
оригинала на
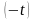 ,
т.е.
,
т.е.
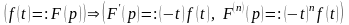 ,
(11)
,
(11)
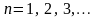 .
.
В самом деле, поскольку – аналитическая функция комплексной переменной в полуплоскости , то ее можно дифференцировать по (под знаком интеграла); получаем
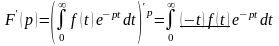 ,
,
т.е.
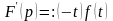 ;
аналогично для
;
аналогично для
 .
.
ПРИМЕР
10. Найти изображение
для оригинала
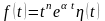 .
.
Решение. Из примера 6 имеем . Применяя правило дифференцирования изображения, получаем
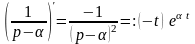 ,
т.е.
,
т.е. 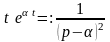 ;
;
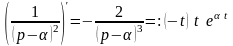 ,
т.е.
,
т.е.
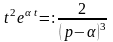 ;
;
после
"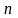 "-кратного
дифференцирования приходим к соотношению
"-кратного
дифференцирования приходим к соотношению
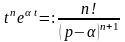 .
.
ПРИМЕР
11. Найти изображение
оригинала
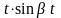 .
.
Решение.
Из примера 7 имеем
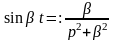 .
Изображение функции
найдем дифференцированием по
функции
.
Изображение функции
найдем дифференцированием по
функции
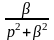 и
умножением этой производной на
и
умножением этой производной на
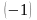 ,
т.е.
,
т.е.
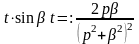 .
.
7. Интегрирование изображения
Если
функция
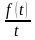 удовлетворяет условиям существования
изображения и
,
то справедливо соотношение
удовлетворяет условиям существования
изображения и
,
то справедливо соотношение
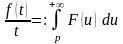 ,
(12)
,
(12)
т.е. интегрированию изображения соответствует деление на оригинала.
Обоснование этого утверждения подробно изложено в [2].
ПРИМЕР
12. Найти изображение
функции
 .
.
Решение.
Имеем
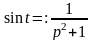 .
В силу соотношения (12) получаем
.
В силу соотношения (12) получаем
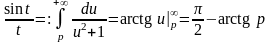 .
.
Применяя операцию интегрирования оригинала, можем записать
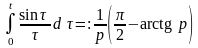 .
.
Задания
Пользуясь простейшими свойствами преобразования Лапласа, получить изображения следующих оригиналов: а)
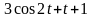 ;
б)
;
б)
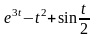 ;
в)
;
в)
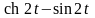 ;
г)
;
г)
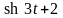 ;
д)
;
д)
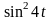 .
.
Ответы:
а)
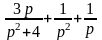 ;
б)
;
б)
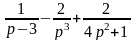 ;
;
в)
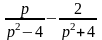 ;
г)
;
г)
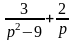 ;
д)
;
д)
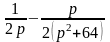 .
.
Для дифференциального уравнения
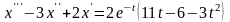
при
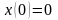 ,
,
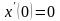 ,
,
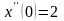 записать соответствующее операторное
уравнение, решить его. Найти решение
дифференциального уравнения.
записать соответствующее операторное
уравнение, решить его. Найти решение
дифференциального уравнения.
Ответ: операторное уравнение имеет вид
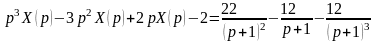 или
или
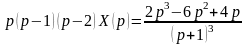 ,
откуда
,
откуда
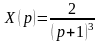 ,
т.е.
,
т.е.
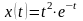 ,
.
,
.
Найти изображение для
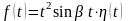 и
и
 .
.
Ответ:
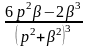 и
и
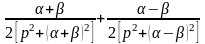 .
.
Теоремы о сдвиге аргументов оригинала и изображения
Теорема (о запаздывании оригинала)
Если
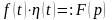 и
и

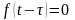 ,
то для
,
то для
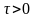 справедливо соотношение
справедливо соотношение
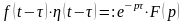 .
(13)
.
(13)
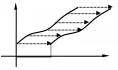 Иначе
говоря, если процесс, описываемый
оригиналом
Иначе
говоря, если процесс, описываемый
оригиналом
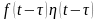 ,
запаздывает на
по сравнению с первоначальным
(см. рисунок), то изображение, соответствующее
этому процессу, получается умножением
изображения первоначального оригинала
на
,
запаздывает на
по сравнению с первоначальным
(см. рисунок), то изображение, соответствующее
этому процессу, получается умножением
изображения первоначального оригинала
на
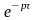 .
В самом деле, для оригинала
.
В самом деле, для оригинала
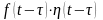 по определению (1) изображение
запишется
в виде
по определению (1) изображение
запишется
в виде
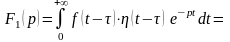
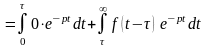 ,
поскольку
для каждого
,
поскольку
для каждого
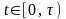 .
Проведем замену переменной
.
Проведем замену переменной
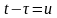 ,
,
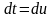 .
Тогда
.
Тогда

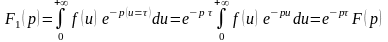 .
.
ПРИМЕР
13. Найти изображение
прямоугольного импульса амплитуды
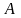 продолжительностью
продолжительностью
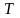 с запаздыванием
с запаздыванием
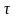 (см. рисунок).
(см. рисунок).
Решение. Импульс
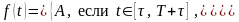
можно записать аналитически с помощью единичной функции в виде
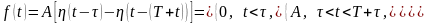
Используя свойства преобразования Лапласа и теорему о запаздывании оригинала, получаем
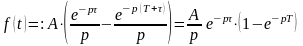 .
.
Замечания:
1. При
использовании теоремы запаздывания
оригинала рекомендуется всегда
оригинал записывать с множителем
.
В противном случае возможны ошибки.
Например, для оригинала
 ,
а для оригинала
,
а для оригинала
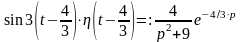 .
.
2. Теорема запаздывания оригинала используется для нахождения изображения кусочно-непрерывных функций (иногда их называют "склеенными" функциями).
ПРИМЕР 14. Найти изображение оригинала

Решение.
Можно записать
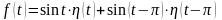 .
Тогда
.
Тогда
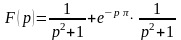 .
.
Здесь
имеем
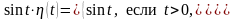 и
и
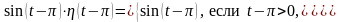 Суммируя
эти функции на промежутках
Суммируя
эти функции на промежутках
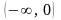 ,
,
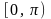 ,
,
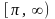 ,
получаем значение функции
.
,
получаем значение функции
.
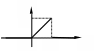 ПРИМЕР
15. Найти изображение
функции, представленной графиком на
рисунке.
ПРИМЕР
15. Найти изображение
функции, представленной графиком на
рисунке.
Решение. Функция
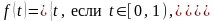 может
быть представлена через единичную
функцию
,
а именно
может
быть представлена через единичную
функцию
,
а именно
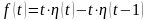 .
Для того, чтобы применить теорему о
запаздывании оригинала, преобразуем
второе слагаемое к виду
.
Для того, чтобы применить теорему о
запаздывании оригинала, преобразуем
второе слагаемое к виду
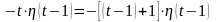 .
Окончательно получаем
.
Окончательно получаем
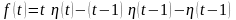 и по формуле (13)
и по формуле (13)
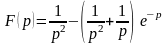 .
.
ПРИМЕР 16. Найти изображение функции, представленной графиком.
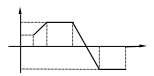 Решение.
По рисунку имеем
Решение.
По рисунку имеем
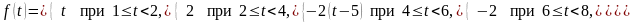 Через
единичную функцию
запишем
так, чтобы на каждом из промежутков
значение
совпало с вышеуказанным, а в точках
"стыка" графика "вводилась"
единичная функция с соответствующим
сдвигом аргумента. Получаем
Через
единичную функцию
запишем
так, чтобы на каждом из промежутков
значение
совпало с вышеуказанным, а в точках
"стыка" графика "вводилась"
единичная функция с соответствующим
сдвигом аргумента. Получаем
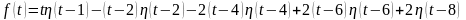 и
соответственно
и
соответственно
 .
.
Теорема (о смещении изображения)
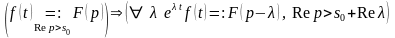 .
(14)
.
(14)
В
самом деле, для оригинала
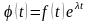 изображение находится по формуле (1)
изображение находится по формуле (1)
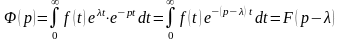 .
.
Число
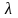 может быть действительным или комплексным,
может быть действительным или комплексным,
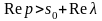 .
.
ПРИМЕР
17. Найти изображение
оригиналов
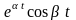 ,
,
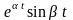 ,
,
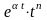 .
.
Решение.
Из примера 7
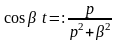 .
По теореме (14) имеем
.
По теореме (14) имеем
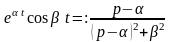 .
.
Аналогично
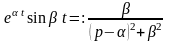 ,
,
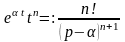 .
.
Задание
Найти изображения функций:
а)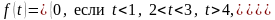 б)
б)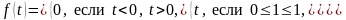
в)
 .
.
Ответы:
а)
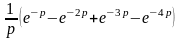 ;
б)
;
б)
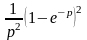 ;
;
в)
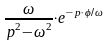 .
.
Найти изображения оригиналов:
а)
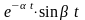 ,
б)
,
б)
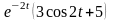 ;
в)
;
в)
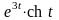 .
.
Ответы:
а)
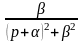 ;
б)
;
б)
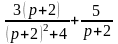 ;
в)
;
в)
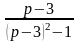 .
.
