2.8 Поверхностные акустические волны в кристаллах

Поверхностные акустические волны (ПАВ) – это упругие волны, распространяющиеся по поверхности вдоль свободной границы. Под свободной поверхностью следует понимать поверхность, находящуюся в вакууме, на которую не действуют какие-либо внешние силы. Поверхность кристалла, соприкасающуюся с воздухом, можно также считать свободной в силу малости акустического сопротивления воздуха. По мере распространения ПАВ переносят энергию вдоль свободной поверхности. Амплитуды смещений в этих волнах экспоненциально убывают по мере удаления от границы. Движение частиц среды происходит по эллиптическим траекториям.

Поверхностные акустические волны широко используются в акустоэлектронных устройствах, поэтому интерес представляет задача о нахождении их параметров с целью расчета и конструирования акустоэлектронных устройств.

Выражения, рассмотренные в предыдущей главе, описывающие отражение и преломление акустических волн на границе кристалла, могут быть использованы также для расчетов параметров поверхностных волн, распространяющихся вдоль свободной границы кристалла диэлектрика. Для этого достаточно положить амплитуду падающей волны равной нулю.

Однако, аналитически задача о распространении ПАВ в анизотропной твердой среде не решается, и для нахождения параметров ПАВ приходится прибегать к численным итерационным методам.

Рассмотрим процедуру поиска пав в кристалле диэлектрика.

Как говорилось ранее, положим амплитуду падающей волны равной нулю. Пусть отражение и преломление акустической волны происходят на поверхности, совпадающей с плоскостью XY.

Алгоритм решения данной задачи будет состоять из следующих этапов:

1. Зададимся некоторым начальным приближенным значением скорости поверхностной волны . Находим значение параметра A._.

2. Запишем уравнение Кристоффеля в виде:

,

откуда определим значения корней .

Появление действительных частей у приводит к изменению смещения в виде экспоненциально затухающей синусоиды. Такие волны получили название обобщенных поверхностных волн.

Решениям текущей задачи о распространении ПАВ вдоль свободной границы кристалла будут соответствовать три корня с отрицательной мнимой частью.

3. Так как , то выражения для смещений можно записать в следующей форме:

.

Из этого выражения найдем для каждого из трех найденных корней уравнения Кристоффеля компоненты единичного вектора поляризации .

4. Далее составим систему граничных условий

и вычислим ее определитель . Найденная система однородных уравнений будет иметь ненулевые решения, если её определитель равен нулю .

5. Если определитель системы граничных условий равен нулю , то искомая скорость ПАВ найдена и равна значению, которое было задано в п. 1. Если же условие равенства нулю не выполняется, необходимо повторить пп. 1-5, изменяя параметр A путем изменения значения до тех пор, пока равенство нулю не будет достигнуто.

Решение будет иметь вид:

,

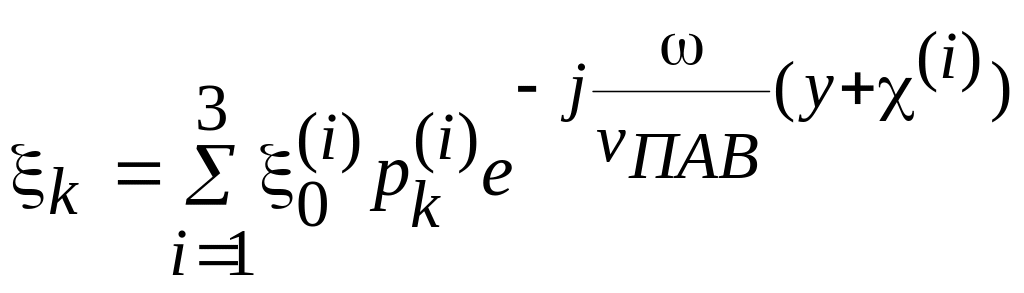то есть решение есть линейная комбинация трёх волн, распространяющихся с одинаковой скоростью .

Вектор плотности потока энергии поверхностных волн на границе кристалла параллелен свободной поверхности. Направление переноса энергии, как и для объемных волн, в общем случае не совпадает с направлением волнового вектора.