2.2 Анализ решений уравнений, описывающих распространение упругих волн в кристаллах

Поскольку различные волновые поля могут быть представлены в виде суперпозиции плоских гармонических волн, в дальнейшем будем рассматривать этот простейший случай. Поэтому решение уравнений (1.4) запишем в виде:

, (1.9)

Где - амплитуда; - компоненты смещения; - круговая частота; - компоненты волнового вектора направляющие косинусы которого равны ; - фазовая скорость волны. Реальный физический смысл имеет вещественная часть (1.9), т. е. . Однако практически удобно производить аналитические выкладки, используя символическую форму записи . Подстановка (1.9) в уравнения (1.4) приводит к следующей системе трёх однородных уравнений:

Введя символ Кронекера , последнее выражение можно переписать в виде:

. (1.10)

Здесь принято обозначение

. (1.11)

Заменив на и обозначив

. (1.12)

Получаем другую форму записи системы уравнений (1.10):

. (1.13)

(1.10) и (1.13) называются уравнениями Кристоффеля, а тензоры второго ранга и тензорами Кристоффеля для данного направления распространения волны. Вследствие симметрии тензора относительно перестановки индексов и , и , и , тензоры и симметричны.

Последнее означает, что и .

Так как компоненты часто используются в численных расчётах, приведём их развёрнутые значения в общем случае триклинного кристалла:

(1.14)

В соотношениях (1.14) использована матричная форма записи модулей упругости . Индексы получаются путём замены индексов тензора по следующему правилу:

Система уравнений (1.13) имеет отличные от нуля решения, если её определитель равен нулю:

.(1.15)

Выражение (1.5) можно рассматривать как уравнение третьей степени относительно . Причём определяемые из (1.15) величины называются собственными значениями тензора . Можно показать, что вследствие симметрии тензора Кристоффеля все три значения , а следовательно, и фазовые скорости являются положительными вещественными числами [2]. Физически это значит, что вдоль любого направления в кристалле возможно распространение трёх волн с различными скоростями. Напомним, что единичный вектор , перпендикулярный поверхности равных фаз, называется волновой нормалью. Поэтому три волны, отвечающие данному , являются изонормальными.

Найдя из (1.15) фазовые скорости трёх изонормальных волн , с помощью (1.13) определяем пространственные ориентации соответствующих векторов смещения . Здесь – единичный вектор, параллельный смещению . Перепишем систему линейных однородных уравнений (1.13) в виде:

(1.16)

дополним его условием нормировки направляющих косинусов (1.17).

(1.16) и (1.17) определяют с точностью до знака. Реально знак смещения зависит от фазы колебательного процесса.

Для определённости условимся в дальнейшем выбирать направление таким образом, чтобы угол между и был минимальным. Численные расчёты показывают, что в кристаллах в общем случае не параллельно и не перпендикулярно направлению волновой нормали . Волна, вектор смещения которой образует наименьший угол с , называется квазипродольной волной, а две другие квазипоперечными. Условием существования чисто продольной волны является (1.18), а чисто поперечной (1.19).

В заключение докажем, что векторы смещения трёх изонормальных волн взаимно перпендикулярны. Пусть фазовым скоростям и изонормальных волн отвечают векторы смещения с направлениями и . Согласно (1.16) они удовлетворяют соотношениям:

(1.20)

(1.21)

Умножим (1.20) на ,(1.21) на и произведём суммирование по . В результате получим:

; (1.22)

. (1.23)

Вычтем из (1.22) (1.23)

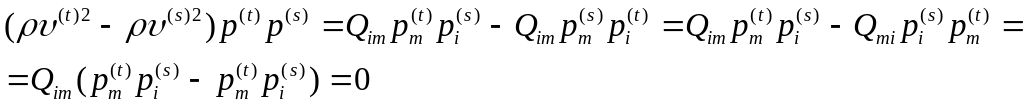
Отсюда или , если и - не определено, если .Физически эти результаты означают, что плоские волны в кристаллах обычно линейно поляризованы (смещение в любой волне параллельно некоторому направлению). Исключение возможно в случае равенства скоростей двух волн. Легко видеть, что вследствие неопределенности уравнения (1.16) не определяют пространственной ориентации и , исключая условия перпендикулярности и смещению третьей волны с фазовой скоростью (здесь полезно отметить, что для любого I скорости всех волн в кристалле не могут быть равны друг другу [2]). Поэтому две такие волны и всегда можно заменить одной с вектором смещения (вырожденный случай). При этом результат сложения даст линейно поляризованную волну, если исходные линейно поляризованные волны имеют одинаковые фазы. Наличие фазового сдвига приводит к тому, что конец вектора смещения будет описывать не отрезок прямой линии, а в общем случае эллипс [2]. Результирующая волна называется эллиптически поляризованной. Частными случаями эллиптической поляризации являются круговая и линейная.

Рис.1:

а – чисто продольная ( ) и чисто поперечные ( ) волны;

б – квазипродольная ( ) и квазипоперечные ( ) волны;

в – вырожденный случай ( ), линейная поляризация.

На рис. 1 показано расположение векторов смещения в разных случаях.