Анализ скорости распространения акустических волн в пьезополупроводниках

Рассмотрим два предельных случая:

1.

Тогда фазовая скорость пьезополупроводника:

Построим график зависимости скорости акустической волны от частоты :

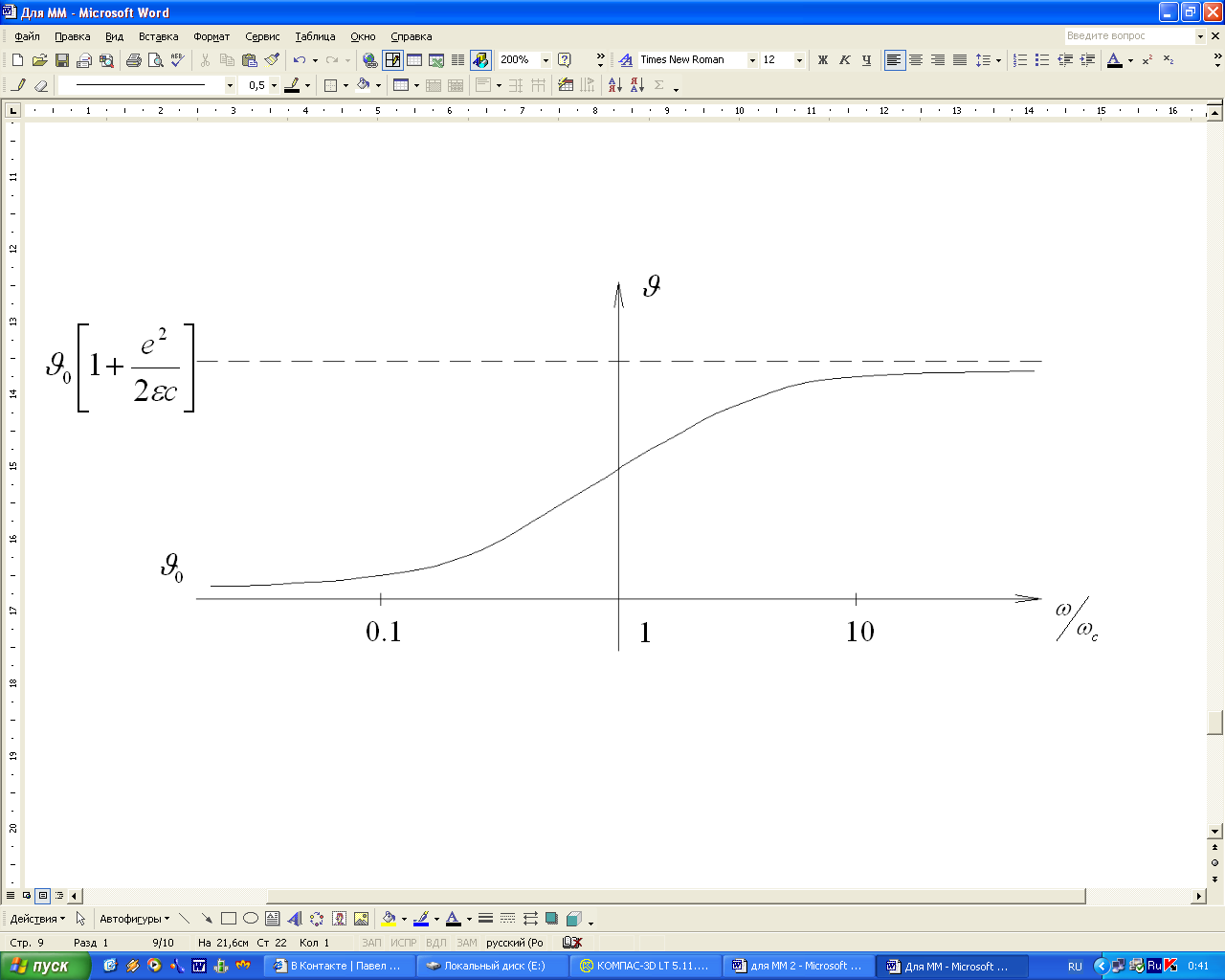
Из графика видно, что в пьезополупроводниках наблюдается дисперсия скорости звука, то есть ее зависимость от частоты.

2.

Построим график зависимости :

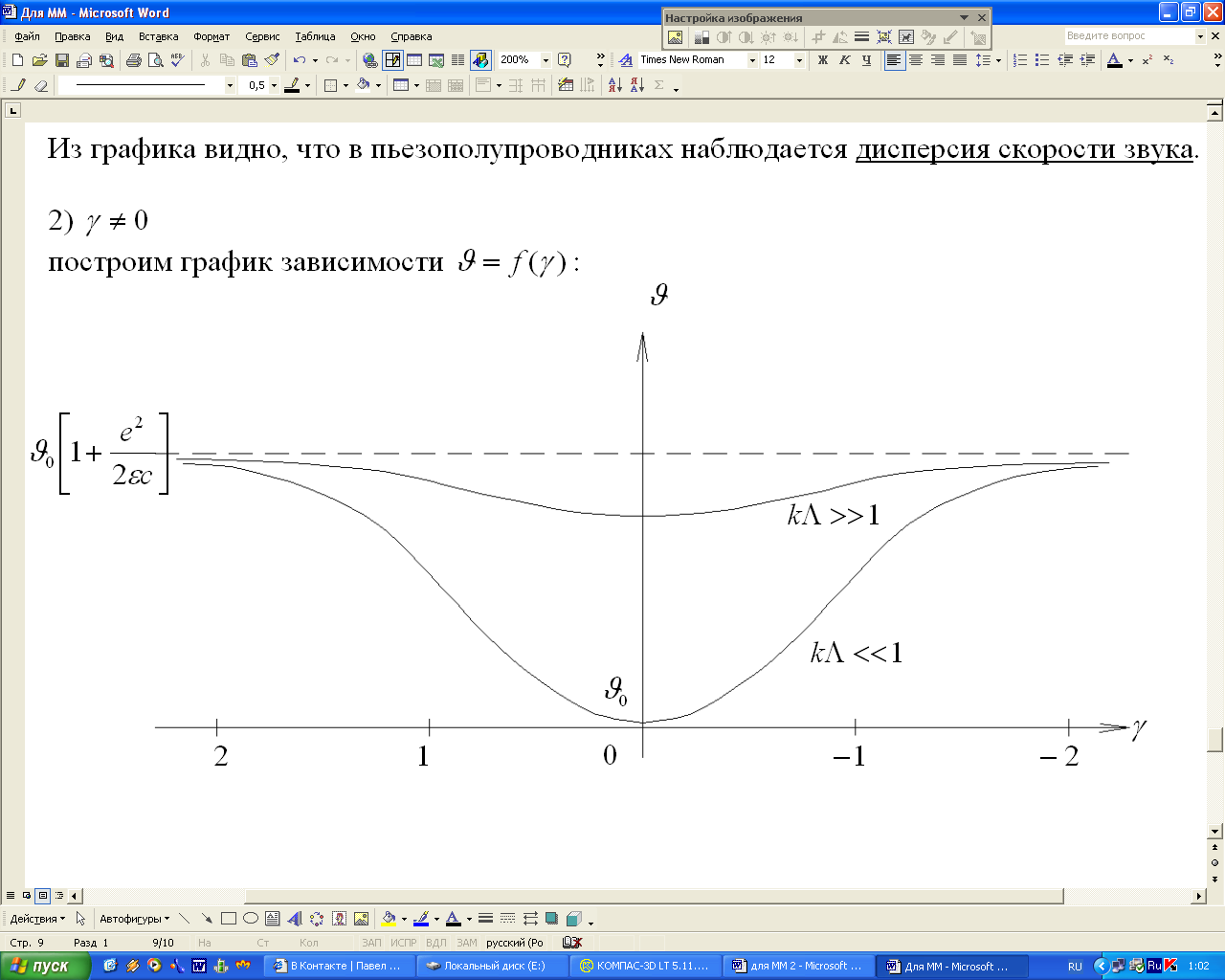
Введем некоторый параметр:

,

где - Дебаевский радиус экранирования. Тогда для четко выражены сгустки электронов, взаимодействия эффективны. Для сгустки размыты из-за теплового движения электронов, взаимодействия не эффективны.

Анализ затухания (усиления) акустических волн в пьезополупроводниках

Запишем коэффициент затухания для пьезополупроводников в виде:

Рассмотрим два предельных случая:

1.

Коэффициент затухания будет иметь вид:

.

Построим график зависимости коэффициента затухания от частоты:

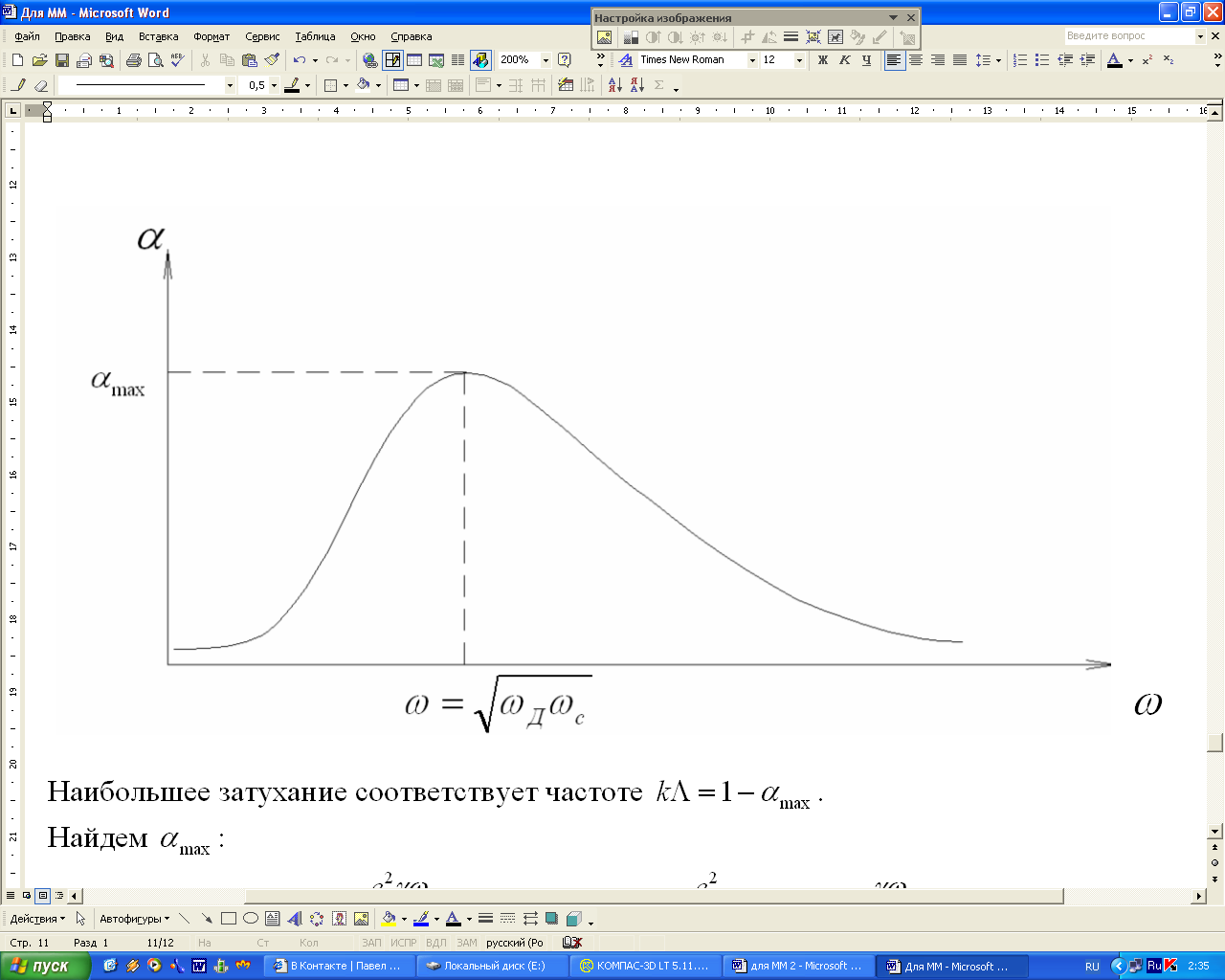
Из графика видно, что наибольшее затухание соответствует частоте .

Найдем :

(9)

Рассмотрим отдельно выражение . Разделив оба слагаемых на , получим . Приравнивая полученное выражение к нулю, получим значение параметра дрейфа при максимальном значении коэффициента затухания:

,

подставим это значение в уравнение (9) и получим:

.

Если учесть, что , окончательно получим:

2.

Построим график зависимости коэффициента затухания от параметра дрейфа γ:

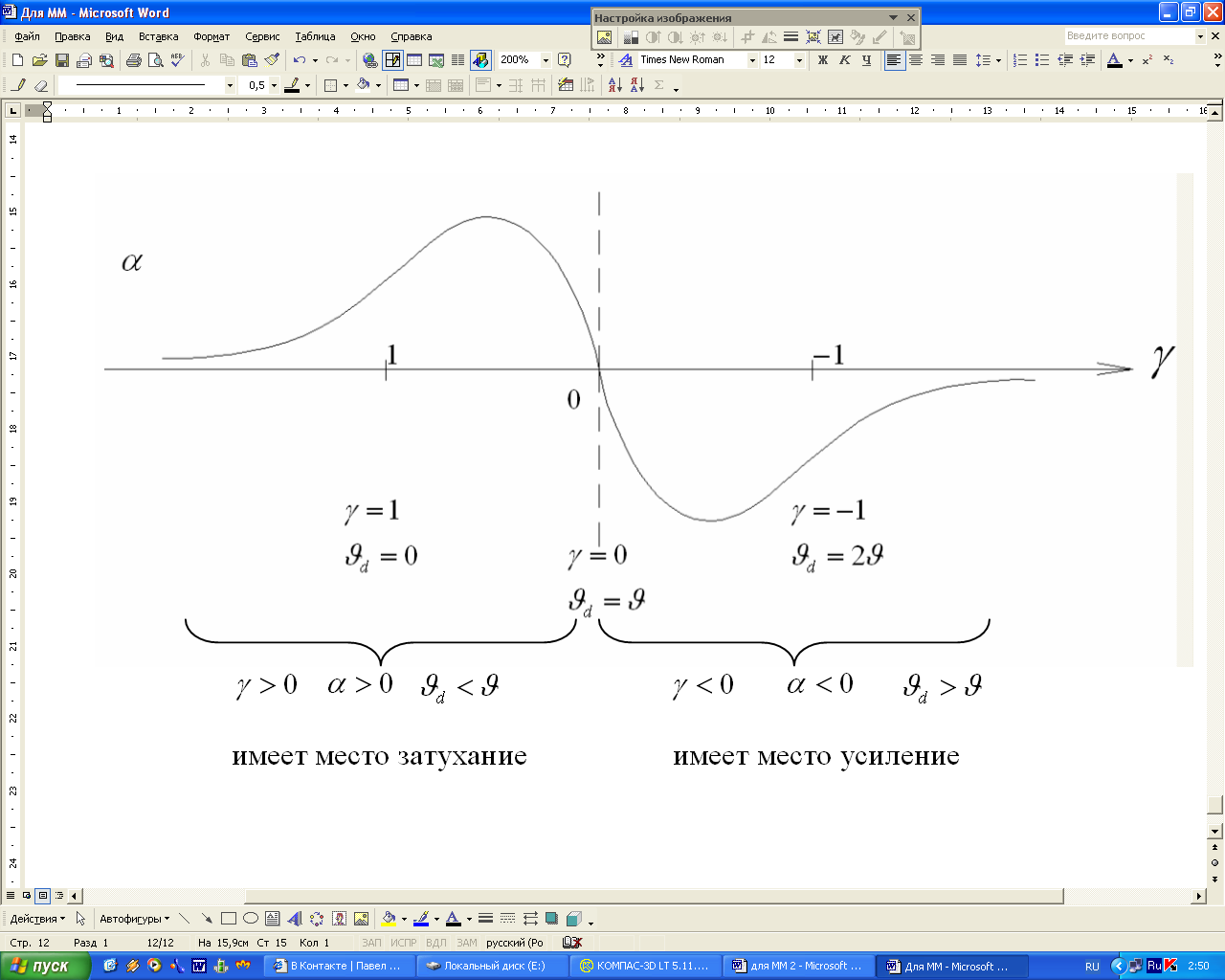
Из графика видно, что при различных значениях параметра дрейфа γ изменяется соотношение между скоростями акустической волны и подвижных носителей заряда. В результате, в зависимости от этих соотношений, в различных областях можно наблюдать как ослабление акустической волны, так и ее усиление. Эта особенность широко используется при создании различных акустоэлектронных устройств.

§5 ОСНОВЫ АКУСТООПТИКИ

Акустооптика – раздел физики, изучающий взаимодействие ультразвуковых волн с электромагнитными волнами (акустооптическое взаимодействие), а также раздел техники, в рамках которого разрабатываются и исследуются приборы, использующие акустооптическое взаимодействие (акустооптические приборы).

Фотоупругость

Связь между колебаниями решетки и световой волной обусловлена фотоупругостью. Показатель преломления прозрачного материала является функцией не только внешнего электрического поля, но и механического напряжения, приложенного к кристаллу. Напряжение вызывает в кристалле деформацию, которая может изменить поляризацию, а, следовательно, и показатель преломления. Таким образом, оптические свойства кристалла изменяются под действием напряжения.

Скорость света в среде, как известно, определяется соотношением:

,

где и – диэлектрическая и магнитная проницаемость соответственно.

Скорость света в вакууме:

ε₀ = 8.85418782*10^-12 Ф/м

μ₀ = 1.25663706144*10^-6 Гн/м

Показатель преломления – величина, равная отношению фазовых скоростей света электромагнитных волн) в вакууме и в данной среде.

Показатель преломления в диэлектрических средах:

В анизотропной среде диэлектрические свойства описываются тензором диэлектрической проницаемости :

Обратное соотношение имеет вид:

,

где – тензор диэлектрической непроницаемости.

– минор, получаемый вычеркиванием i-й строки и j-го столбца.

Удобно использовать шесть независимых коэффициентов В для определения эллипсоида показателей преломления, или индикатрисы:

Если оси координат совпадают с главными осями тензора В, то

Для прозрачных (с малой проводимостью) и неферромагнитных кристаллов главные компоненты диэлектрического тензора связаны с компонентами показателя преломления соотношениями:

,

,

.

Следовательно,

И индикатриса имеет вид:

.

Использование индикатрисы полезно по следующим причинам. Для заданной волновой нормали она позволяет простым способом определить показатели преломления и направления электрических смещений. Для нахождения волновых фронтов, которые могут распространяться в кристалле перпендикулярно заданному направлению, следует просто построить сечение, проходящее через центр эллипсоида и перпендикулярно этому направлению. Показатели преломления будут равны большой и малой осям полученного эллипса, а вектор электрического смещения D в каждой плоскополяризованной волне параллелен оси эллипса, определяющей соответствующий показатель преломления.

Акустическая волна в кристалле вызывает малые изменения величины, формы и ориентации эллипса:

,

где – компоненты тензора пьезооптических коэффициентов

– компоненты тензора напряжений

Поскольку , отсюда следует, что . Эти соотношения позволяют использовать сокращенную матричную запись:

m , n = 1, 2, 3, 4, 5, 6

и связаны соотношениями:

n=1, 2 или 3 m=1,2,3…6

т=4, 5 или 6 m=1,2,3…6

В общем случае .

Более удобно использовать упругооптические коэффициенты p_ijrs, которые связывают изменения В с деформацией u_rs

.

Пьезооптические и упругооптические коэффициенты связаны через модули упругости:

Эти коэффициенты являются безразмерными. Можно использовать сокращенные матричные обозначения:

n, m = 1, 2, 3, … 6

В этом случае

Произведение диэлектрической проницаемости и диэлектрической непроницаемости равно единице:

,

где - символ Кронекера

_ij⁰ – тензор диэлектрических проницаемостей при отсутствии деформации

Продифференцировав соотношение , получим:

Или:

Заменим индекс j на l в левой части уравнения

и домножим обе части уравнения на

Таким образом, переход в тензорной форме от относительного изменения диэлектрической непроницаемости к относительному изменению диэлектрической проницаемости осуществляется, исходя из соотношения:

Или:

,

где - амплитудное значение деформации.

Для действующего значения фотоупругой константы и амплитудного значения деформации:

.

Дифракция света на ультразвуке

Обозначения:

k, ω, λ – волновое число, частота и длина световой волны соответственно;

K, Ω, Λ – волновое число, частота и длина ультразвуковой волны соответственно.

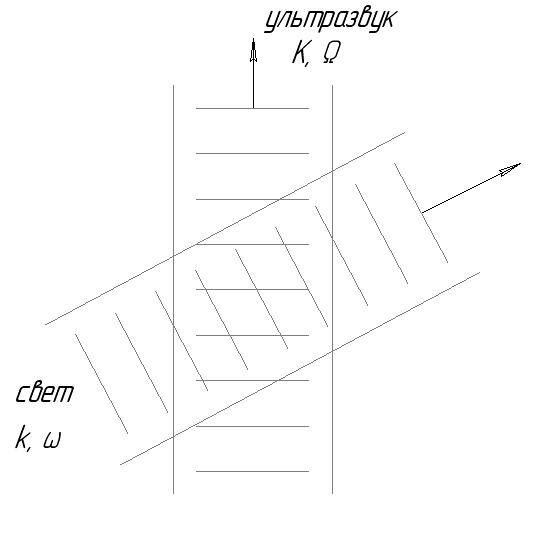
Различают 2 вида дифракции света на ультразвуке:

1. Дифракция Рамана-Ната

2. Дифракция Брэгга

Дифракция Рамана-Ната

Такая дифракция имеет место на низких частотах, т.е. при , где L – ширина ультразвукового пучка, пересекаемого светом (глубина взаимодействия). Необходимо, чтобы свет падал параллельно или под очень малым углом к фронту ультразвуковой волны.

Ультразвуковая волна действует как фазовая дифракционная решетка, и прошедший через нее свет характеризуется синусоидальным изменением фазы в плоскости, перпендикулярной направлению пучка света. В результате возникает дифракционная картина со многими порядками по обе стороны от пучка нулевого порядка.

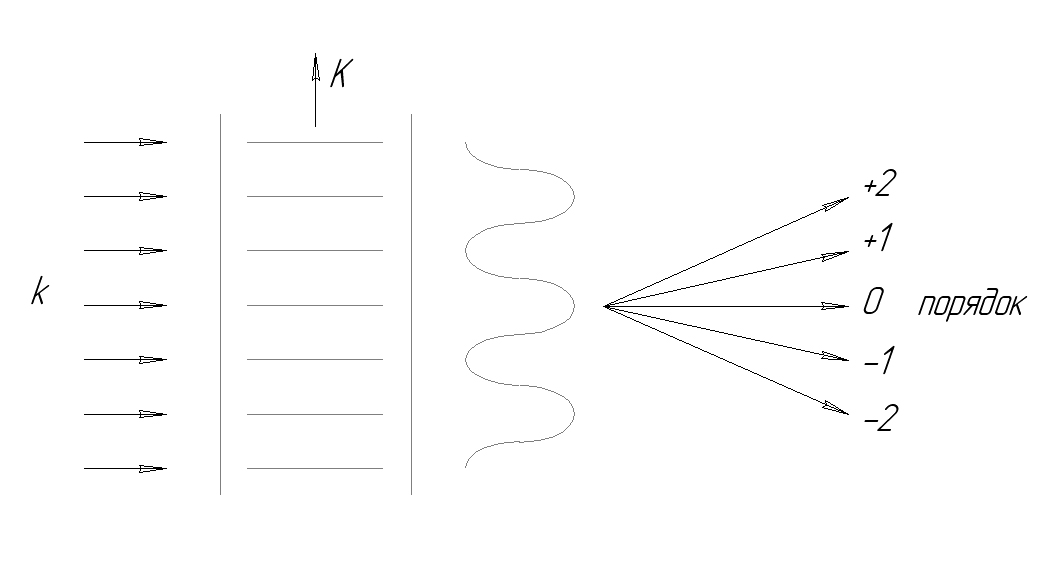
m – номер максимума

Дифракция Брэгга

Такая дифракция имеет место на высоких частотах, т.е. при . Она возникает, если свет падает на звуковой пучок под определенным углом θ, т.н. углом Брэгга:

В этом случае отклонение света происходит только в первый порядок дифракции. Объяснить дифракцию Брэгга можно тем, что падающая под углом к звуковой решетке световая волна частично отражается от нее и интерференция отраженных лучей определяет интенсивность дифрагированного света.

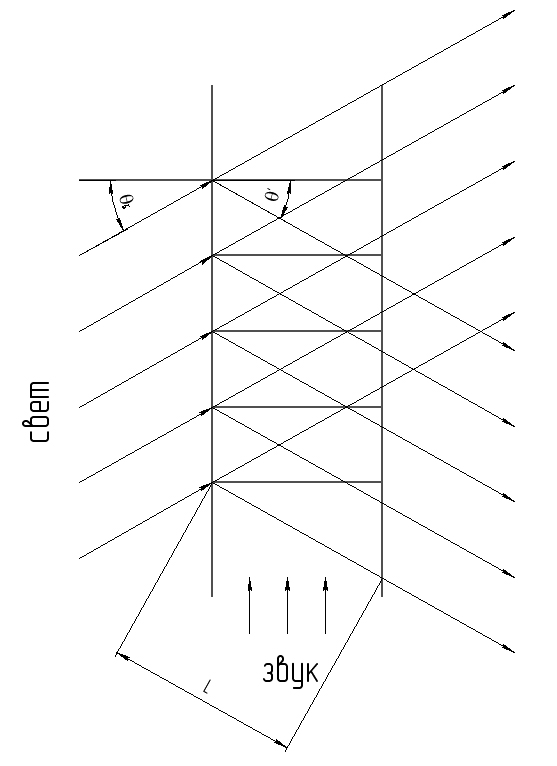
Интерференционная картина возникает лишь в том случае, если пучки, отраженные от соседних максимумов звуковой волны, пересекаются, т.е. выполняется условие:

В зависимости от того, какой угол – тупой или острый образует волновой вектор света с направлением распространения звуковой волны, частота дифрагированного света равна (+1-й порядок дифракции) либо (-1-й порядок дифракции).

Дифрагированный луч выходит из звукового пучка под углом ; в изотропной среде .

В изотропной среде скорость света со всех направлениях одинакова, и можно описать окружность радиусом k вокруг треугольника со сторонами k, k’, K. Свет будет дифрагировать только под тем углом и для той длины волны, для которой существует этот треугольник.

Может быть рассмотрен случай, когда пучок света расширяется, т.е. имеет набор волновых векторов. Управляя частотой (а, следовательно, и волновым числом K) ультразвука, можно подбирать под каждый из волновых векторов электромагнитной волны свое значение K и наблюдать дифракцию под разными углами (производить сканирование в угловом секторе).