2.7 Колебательное звено.

 

Это звено называют также инерционным звеном второго порядка.

Уравнение динамики инерционного звена второго порядка имеет вид:

,

где - постоянные времени,  - коэффициент усиления (или передачи).

В зависимости от вида корней характеристического уравнения инерционное звено второго порядка может иметь различные переходные характеристики. Это позволяет установить две разновидности звена – апериодическое и колебательное. В случае вещественных корней получаем апериодическое звено второго порядка, которое эквивалентно последовательному соединению двух апериодических звеньев первого порядка.

Если корни характеристического уравнения комплексные, то инерционное звено второго порядка называется колебательным. В данном случае разложение звена на простейшие возможно, но получается довольно сложным и малополезным для практических целей. Поэтому колебательное звено относится к элементарным звеньям.

1. Передаточная функция. Частотные и временные характеристики звена.  Уравнение динамики колебательного звена имеет вид:

.

Перейдем к операторной форме записи уравнения, для этого применим преобразование Лапласа при нулевых начальных условиях:  

,

.

Передаточная функция  колебательного звена

.

Характеристическое уравнение для  данного звена запишется:

,

,

.

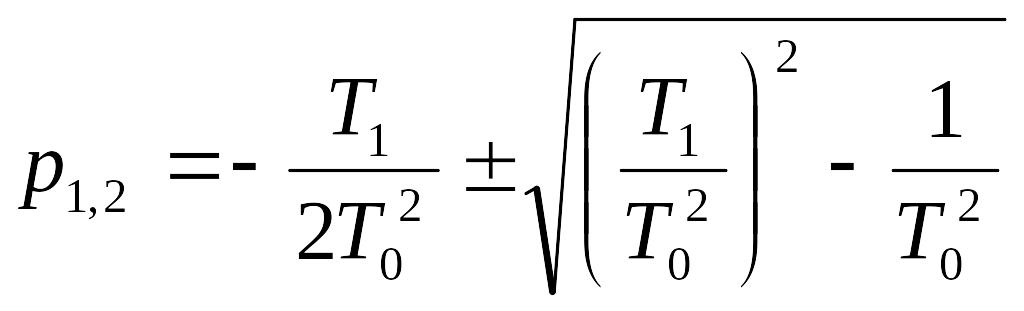Частотные характеристики получаются путем замены в выражении передаточной функции комплексной переменной  на  :

.

Годограф изображен на рис. 33. Амплитудно-фазовые характеристики  приведены для разных значений  и .

Графики ЛАЧХ и ФЧХ  данного звена представлены на рис. 34.

Переходная характеристика  (рис. 35) для колебательного звена при комплексных корнях р₁ и р₂:

,

,

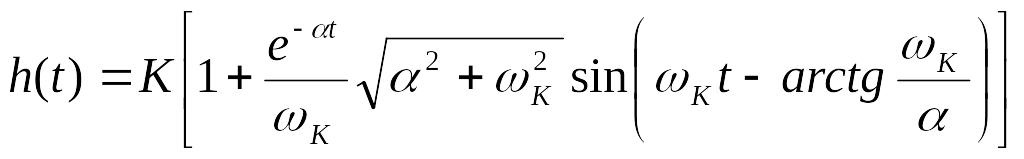где

 

 

.

Весовая функция определяется как (рис. 36):

.

Пусть

,

,

тогда

.

 

  2. Примеры  колебательного звена.

-        Центробежный маятник.

-        Контур, содержащий ,  и  .

-        Электромагнитный усилитель поперечного поля.

-        Электродвигатель постоянного тока (если входом является напряжения якорной цепи, а выходом – скорость вращения при учете постоянной времени якоря и электромеханической постоянной времени).

 

2.8 Дифференцирующее звено.

Дифференцирующие звенья реагируют на скорость изменения входного воздействия и могут быть описаны дифференциальными уравнениями, содержащими в правой части производную от входной переменной. Левая часть уравнения может иметь любой собственный оператор подобно рассмотренным выше звеньям. Рассмотрим наиболее общие случаи уравнений дифференцирующих звеньев:

,                                          (*)

,                                   (**)

,                           (***)

где - постоянная времени,  - коэффициент усиления (или передачи).

Уравнение (*) соответствует идеальному (безынерционному) дифференцирующему звену; (**) - реальному (инерционному) дифференцирующему звену без статизма; (***) - реальному ( инерционному) дифференцирующему звену со статизмом (или пропорционально-дифференцирующему звену). Рассмотрим идеальное дифференцирующее звено.

1. Передаточная функция. Частотные и временные характеристики звена.  Уравнение динамики дифференцирующего звена имеет вид:

.

Перейдем к операторной форме записи уравнения, для этого применим преобразование Лапласа при нулевых начальных условиях:  

.

Передаточная функция  идеального звена

.

Частотные характеристики получаются путем замены в выражении передаточной функции комплексной переменной  на  :

.

Построим годограф (рис. 37), годограф для данного звена совпадает с мнимой положительной полуосью.

Перейдем к показательной форме представления комплексного числа:

.

Тогда ЛАЧХ примет вид: 

,

если , то   

.

ЛАЧХ дифференцирующего звена является прямой линией, проходящей с наклоном   проходящую через точку на оси абсцисс, соответствующей значению , если , прямая проходит через начало координат. 

Определим ФЧХ:

.

Фазо-частотная характеристика для дифференцирующего звена имеет вид прямой линии, параллельно оси абсцисс. Графики ЛАЧХ и ФЧХ представлены на рис. 37.

 

Получим переходную характеристику (рис. 38):

,

.

Весовая функция (рис. 39):

. 

2. Примеры  дифференцирующего звена. Его реализация на операционном усилителе.

-        Электрические цепи, содержащие  или .

-        Демпфер с пружиной.

-        Тахогенератор, предназначенный для дифференцирования угла поворота вала электрической машины. Выходное  напряжение тахогенератора определяется как:

,

где  - угол поворота вала машины.

Схема реализации дифференцирующего звена на операционных усилителях имеет следующий вид (рис.40). Передаточная функция определяется следующим образом:

.

Постоянная времени:

.