Глава 2. Основные динамические звенья систем автоматического управления. Их основные характеристики.

 

Динамическим звеном называют часть системы, которая описывается  дифференциальным (или интегральным) уравнением. В общем случае порядок уравнения может быть произвольным, а звено сколь угодно сложным. Сложные звенья могут быть разложены на простейшие, элементарные звенья. К элементарным звеньям принято относить звенья, которые описываются дифференциальным уравнением не выше второго порядка. Это следующие звенья:

-        пропорциональное (безынерционное) звено;

-        интегрирующее звено;

-        дифференцирующее звено;

-        апериодическое звено;

-        колебательное звено;

-        звено с чистым запаздыванием.

Основные характеристики звеньев и систем делятся на три вида:

1. математическая характеристика (к ней относят передаточную функцию);

2. частотные характеристики (к ним относят амплитудно-фазовую характеристику, график которой называется годограф, амплитудно-частотную характеристику, фазо-частотную характеристику);

3. временные характеристики (переходная характеристика или переходная функция, весовая или импульсная переходная функция).

  

2.1 Основные свойства Преобразования Лапласа, передаточная функция, ее нули и полюса.

1. Преобразование Лапласа. Преобразованием Лапласа называют преобразование функции  переменной  в функцию  комплексной переменной  при помощи интеграла:

,                            (*)

где функция  называется оригиналом, функция  - изображением функции . Равенство  (*) записывают также в виде:

, .

Преобразование Лапласа обладает следующими свойствами:

1.      Линейность.

      - Теорема суперпозиции. Изображение суммы конечного числа   слагаемых есть сумма изображений этих слагаемых:

    ,

 

       - Теорема линейности. Изображение произведения функции на постоянную величину равно произведению изображения функции на эту величину:

  , .

2.       Теорема подобия (изменения масштаба):

  , .

3.      Теорема запаздывания. Если оригинал смещается вдоль оси на постоянную t, то

      .

4.       Теорема смещения:

  , .

 

  5.       Дифференцирование при нулевых начальных условиях:

    .

6.       Дифференцирование при ненулевых начальных условиях:

  ,

    ,

     и т.д.

7.       Интегрирование:

    .

8.       Предельные теоремы:

 = ,

 = .

Предельные теоремы можно использовать, если известно, что  и   существуют.

 

 

Таблица 1. Соответствия между оригиналом

и изображением наиболее распространенных функций.

 

Название функции	Оригинал	Изображение
1. Постоянная величина.	,
2. Степенная  функция.
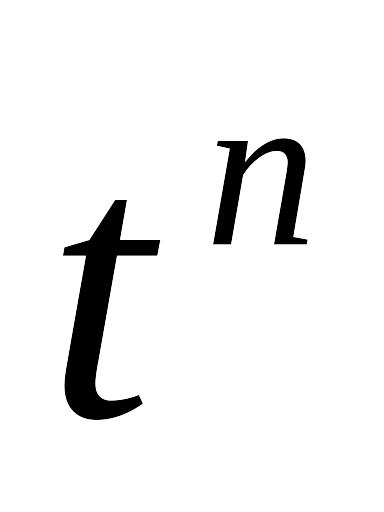
3.  Экспонента,
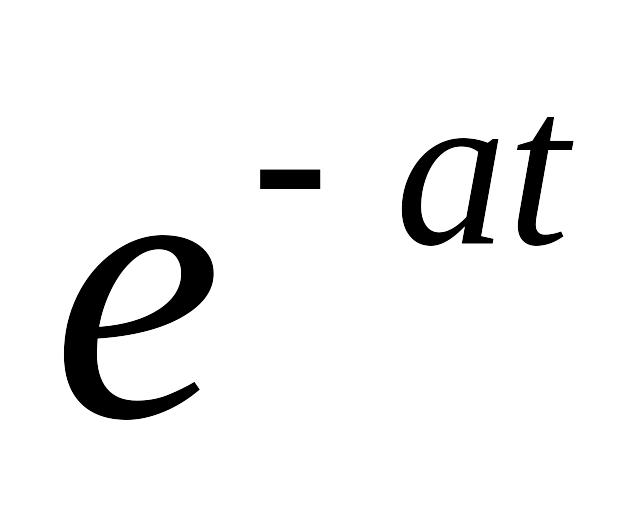
4. Смещенная  экспонента,
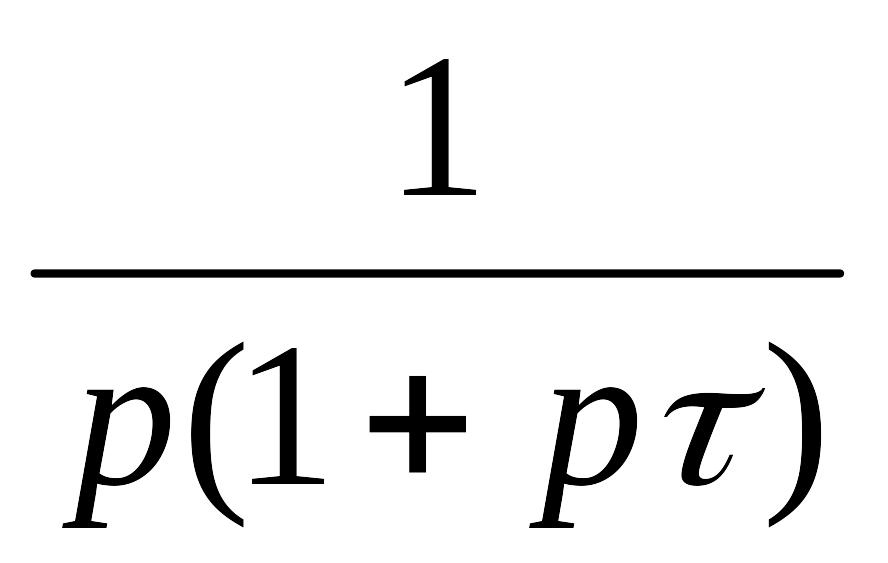
5. Синусоида.
6. Косинусоида.
7. Затухающая синусоида.
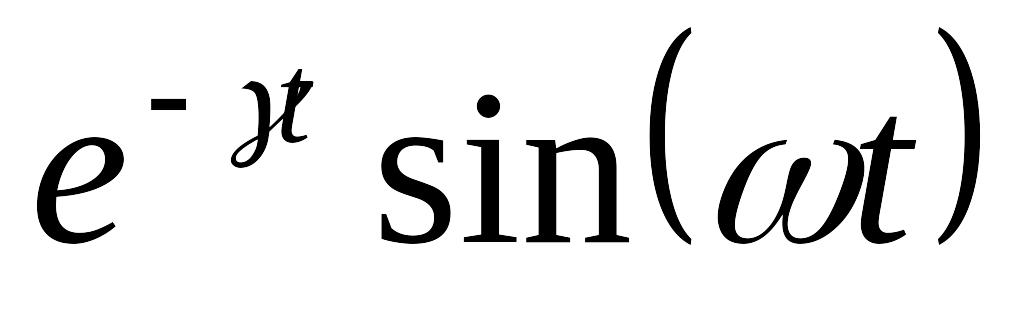
8. -функция.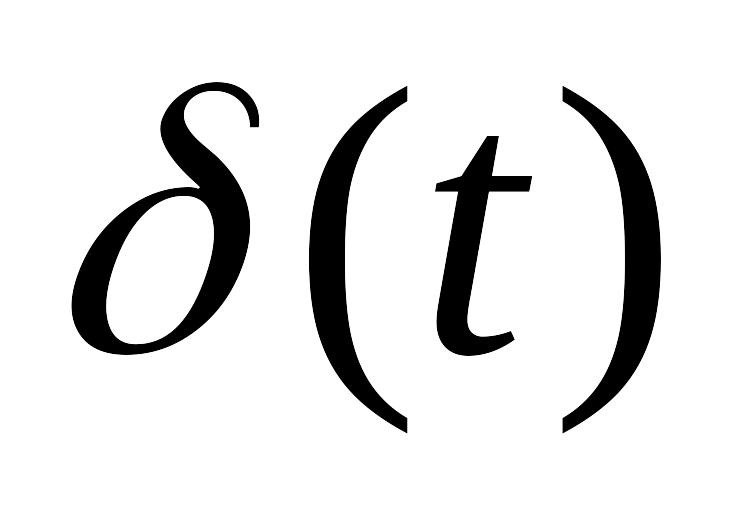		1

 

 2. Передаточная  функция. Рассмотрим некоторую систему:

 - входной сигнал, - выходной сигнал (координата системы). 

Пусть данная система описывается дифференциальным уравнением -го порядка:

.

В реальных системах всегда справедливо следующее неравенство:

.

Дифференциальное уравнение, описывающее систему, записано во временном пространстве. Используя преобразование Лапласа, перейдем в пространство Лапласа, считая начальные условия нулевыми:

 

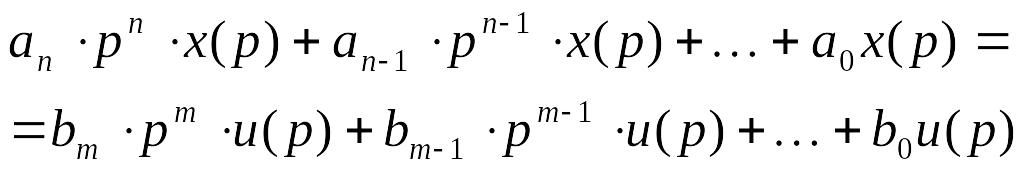
Передаточная  функция это отношение лапласовского изображения выходной величины к лапласовскому изображению входной величины (при нулевых начальных условиях). Согласно этому определению выражение для передаточной функции имеет следующий вид:

,

 

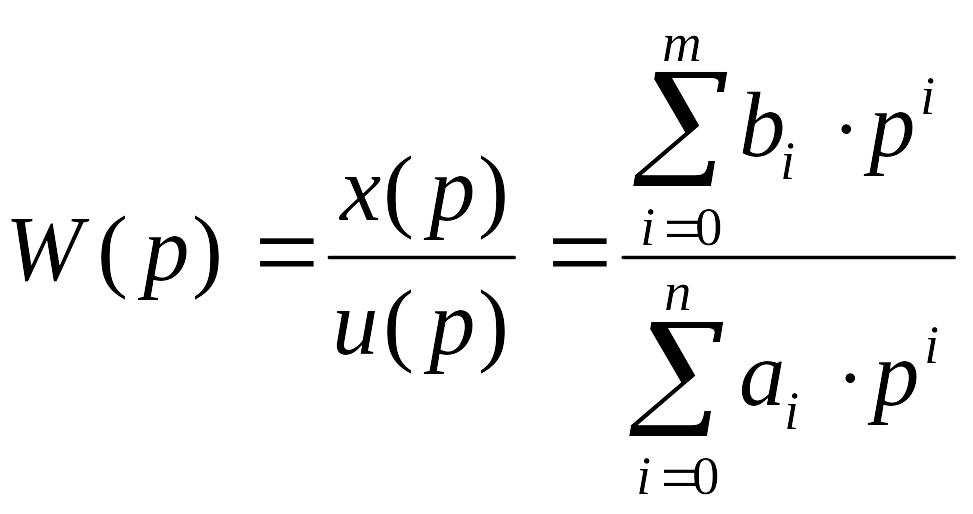т.е. передаточная функция равна отношению операторного полинома, стоящего при входной переменной, к операторному полиному, стоящему при выходной переменной. 

Пример 1. Система описывается  следующим дифференциальным уравнением:

.

Необходимо найти передаточную функцию  системы.

Перейдем в пространство Лапласа; для получения изображений воспользуемся таблицей соответствий:

.

Пример 2. Задано следующее дифференциальное уравнение:

.

Необходимо найти передаточную функцию  системы.

Перейдем в пространство Лапласа:

.

 

Нули передаточной функции - это корни уравнения:

.

Полюса  передаточной функции - это корни уравнения:

.

Нули и полюса делятся на левые и правые. Левые полюса и нули расположены в левой полуплоскости комплексной плоскости, а правые, соответственно, в правой полуплоскости (см. рис.2).

Ранее были рассмотрены односвязные системы, т.е. системы, имеющие один вход и один выход. Но существуют еще и многосвязные системы, имеющие большее число входов и выходов (рис.3).    

Входные сигналы ,  оказывают влияние на каждый из выходных сигналов  и . Связь  между входными и выходными сигналами:

,

в векторной форме:

,

где - передаточная функция многосвязной системы, она определяется как

,  , .
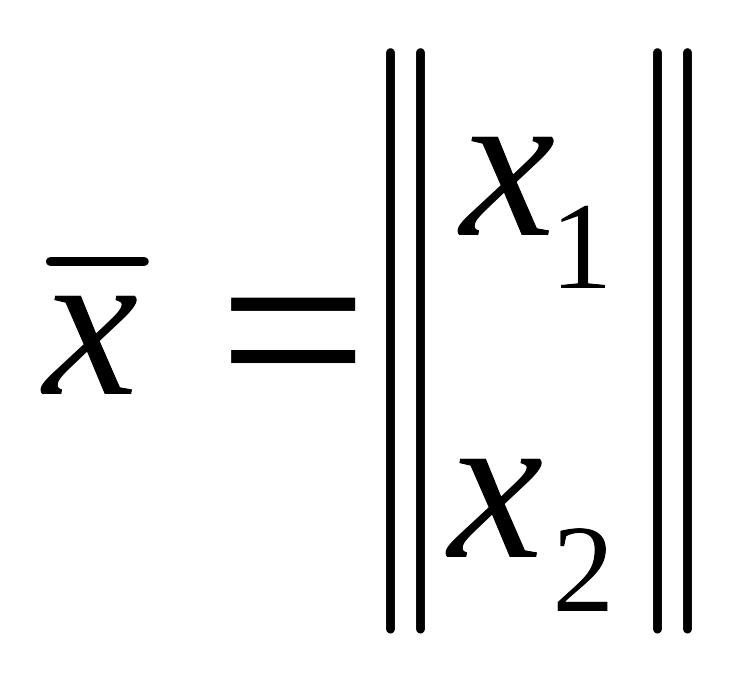