
- •Лекция 5 Постановка краевой задачи теплопроводности
- •Дифференциальное уравнение теплопроводности
- •Уравнение теплопроводности при неоднородных свойствах
- •Уравнение теплопроводности для анизотропных сред
- •Уравнение теплопроводности для высокоскоростных процессов
- •Краевые условия
- •3.7. Безразмерная формулировка краевой задачи теплопроводности
- •3.8. Стационарная теплопроводность плоского слоя
- •Метод регулярного теплового режима расчета нагрева (охлаждения) тел
- •3.10. Теплопроводность при плавлении-затвердевании металла
- •3.11. Метод сквозного счета в задачах теплопроводности при структурных и фазовых переходах
- •3.12. Приближенный учет конвекции жидкого ядра кристаллизующегося слитка
3.10. Теплопроводность при плавлении-затвердевании металла
 Процесс
переноса теплоты может сопровождаться
изменением агрегатного состояния
вещества. В процессе перехода вещества
из одного агрегатного состояния в другое
выделяется либо поглощается большое
количество теплоты. Процесс фазового
перехода может локализоваться в объеме
малой толщины, называемом фронтом
фазового перехода.
Процесс
переноса теплоты может сопровождаться
изменением агрегатного состояния
вещества. В процессе перехода вещества
из одного агрегатного состояния в другое
выделяется либо поглощается большое
количество теплоты. Процесс фазового
перехода может локализоваться в объеме
малой толщины, называемом фронтом
фазового перехода.
В
соответствии с балансом подвода и отвода
теплоты фронт фазового перехода будет
перемещаться с определенной скоростью.
К фронтальным процессам относится и
процесс плавления-затвердевания металла.
На рис. 3.18 показано температурное поле
в отливке с плоским фронтом фазового
перехода. При отводе тепла с поверхности
отливки (x=0)
образуется корка твердой фазы (1) толщиной
ε, которая растет по мере отвода тепла
со скоростью
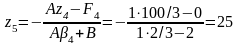 .
Температурное поле в твердой фазе
подчиняется уравнению теплопроводности
.
Температурное поле в твердой фазе
подчиняется уравнению теплопроводности
 ,
(3.90)
,
(3.90)
где а1 – коэффициент температуропроводности твердой фазы металла.
В жидкой фазе 2 температурное поле описывается системой дифференциальных уравнений переноса энергии
 ,
(3.91)
,
(3.91)
движения вязкого расплава
 (3.92)
(3.92)
и неразрывности
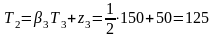 ,
(3.93)
,
(3.93)
где
 – вектор скорости;
– вектор скорости;
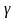 – градиент давления; а2,
ρ2
– коэффициент температуропроводности
плотность жидкой фазы металла.
– градиент давления; а2,
ρ2
– коэффициент температуропроводности
плотность жидкой фазы металла.
На границе фазового перехода (на рис. 3.18 это граница x = ε) плотности тепловых потоков в твердой и жидкой фазах равны и связаны со скоростью продвижения границы соотношением
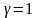 ,
(3.94)
,
(3.94)
 где
L
[Дж/кг] – удельная теплота фазового
перехода; плотность ρ относится к
исходной фазе: при затвердевании металла
это плотность жидкой фазы, при плавлении
– к твёрдой.
где
L
[Дж/кг] – удельная теплота фазового
перехода; плотность ρ относится к
исходной фазе: при затвердевании металла
это плотность жидкой фазы, при плавлении
– к твёрдой.
Таким образом, постановка задачи включает уравнение теплопроводности для твердой фазы (3.90), систему уравнений тепломассопереноса (3.91–3.93) в жидкой фазе и баланс тепловых потоков на границе раздела фаз (3.94). Задача замыкается другими рассмотренными ранее краевыми условиями, включающими начальное распределение температуры и поля скоростей жидкой фазы, условия теплообмена на поверхности слитка (x=0) и на оси симметрии (x=δ), условия «прилипания расплава» на границе фазового перехода.
Рассмотрим задачу затвердевания плоского слоя из не перегретого неподвижного расплава, имеющего постоянную температуру Тзат (рис. 3.19). Поскольку на левой поверхности слоя поддерживается постоянная температура Тп<Тзат, происходит затвердевание расплава, т.е. формируется во времени корочка твердой фазы толщиной ε. При этом на подвижной границе затвердевания x = ε выделяется удельная теплота фазового перехода L [Дж/кг].
Математическая формулировка задачи включает дифференциальное уравнение теплопроводности
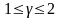 (3.95)
(3.95)
начальное условие
Т(x, 0) = Тзат; ε(0) = 0, (3.96)
граничные условия
Т(ε, τ) = Тпл ; Т(0, τ) = Тп , (3.97)
а также условие выделения тепла на границе фазового перехода
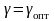 .
(3.98)
.
(3.98)
Принимая линейный закон распределения температуры по толщине твердой фазы в любой момент времени, из условия (3.98) получаем
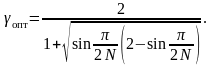 .
.
После разделения переменных и интегрирования получаем решение задачи
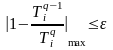
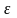
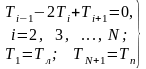 .
(3.99)
.
(3.99)

Решение (3.99) отражает «закон квадратного корня» роста корки твердой фазы при затвердевании слитка (рис. 3.20), в соответствии с которым скорость роста твердой фазы уменьшается с течением времени. Это объясняется возрастающим тепловым сопротивлением растущей корки, через которую отводится теплота фазового перехода.
 Пример
3.
Непрерывный плоский стальной
слиток (сляб) толщиной 2δ=20 см вытягивается
со скоростью 0,6 м/мин из неподвижного
кристаллизатора (рис. 3.21).
Температура поверхности сляба
поддерживается постоянной, Тп
=
900оС.
Свойства
стали: L=275
кДж/кг; ρ = 7800 кг/м3;
λ = 45 Вт/(м·К); Tпл
= 1500оС.
Определить протяженность двухфазной
зоны l
по длине слитка.
Пример
3.
Непрерывный плоский стальной
слиток (сляб) толщиной 2δ=20 см вытягивается
со скоростью 0,6 м/мин из неподвижного
кристаллизатора (рис. 3.21).
Температура поверхности сляба
поддерживается постоянной, Тп
=
900оС.
Свойства
стали: L=275
кДж/кг; ρ = 7800 кг/м3;
λ = 45 Вт/(м·К); Tпл
= 1500оС.
Определить протяженность двухфазной
зоны l
по длине слитка.
Решение. Из уравнения (3.99) определим время окончания затвердевания, за которое толщина корки достигнет половины толщины сляба (ε=δ)
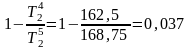
Протяженность
двухфазной зоны
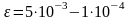 .
.
