3.7. Безразмерная формулировка краевой задачи теплопроводности

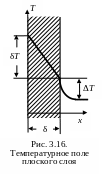
Рассмотрим одномерную нестацио­нарную задачу теплопроводности при граничных условиях 3-го рода, моделирующую температурное поле в плоском слое. Для записи краевой задачи теплопроводности

, ,

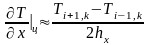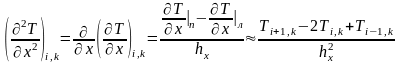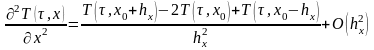(3.76)

выберем безразмерные переменные: температуру и координату 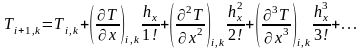. Размерные переменные и 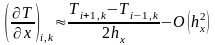подставим в дифференциальное уравнение

.

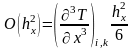
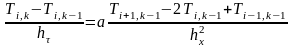Здесь 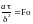– число Фурье, характеризует безразмерное время процесса теплопроводности, его называют числом гомохронности (однородности по времени). Если для двух систем характерная длительность 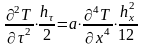имеет одно и то же значение, то гомохронность переходит в синхронность.

Итак, безразмерная форма дифференциального уравнения теплопроводности

. (3.77)

Применим такое же обезразмеривание к граничным условиям 3-го рода

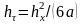
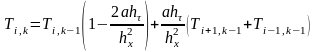
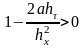
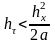
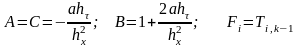
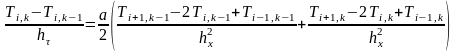
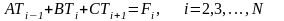
, (3.78)

где 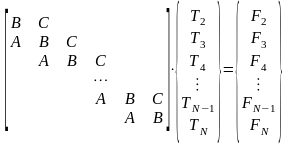– число Био, характеризующее отношение температурного перепада δТ к температурному напору ΔТ.

Действительно,

.

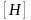
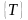
При малых числах Био, когда температурный перепад меньше температурного напора (δТ < ΔТ), в теплообмене большую роль играет условие теплообмена на гра­ни­це, т.е. внешнее тепловое сопротивление. При больших числах Био, когда темпе­ра­тур­ный перепад больше температурного напора (δТ > ΔТ), в теплообмене большую роль играет теплопроводность, т.е. внутреннее тепловое сопротивление плоского слоя.

3.8. Стационарная теплопроводность плоского слоя

В частном случае для плоского слоя толщиной δ, не содержащего внутренних источников тепла (q_V=0), на поверхностях которого x=0 и x=δ заданы граничные условия первого рода, т.е. поддерживаются температуры соответственно Т₁ и Т₂. Математическая формулировка стационарной краевой задачи теплопроводности имеет вид

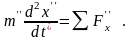(3.79)

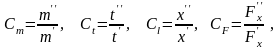(3.80)

Общее решение уравнения теплопроводности (3.79) получается после двойного интегрирования

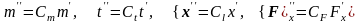
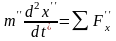
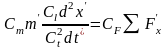
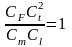. (3.81)

Постоянные интегрирования С₁ и С₂ находятся подстановкой граничных условий (3.80) в общее решение (3.81)

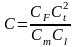(3.82)

и имеют вид

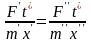. (3.83)

В результате получается решение задачи

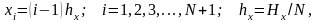, (3.84)

дающее линейное распределение температуры по толщине слоя.

Плотность теплового потока определяется в соответствии с законом Фурье

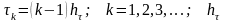(3.85)

и является постоянной, отношения 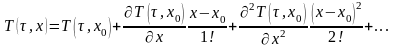и называются соответственно тепловой проводимостью и тепловым сопротивлением плоского слоя.

Потери тепла через плоскую стенку

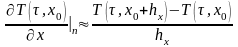. (3.86)

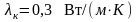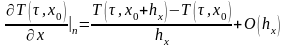Пример 1. Определить потери тепла через кирпичную стенку ( ) площадью 3х5 м за сутки. Как изменится теплопровод­ность, если кирпичную стенку заменить деревянной (сосна поперек волокон, ). Толщины стенок составляют δ_к= δ_д=25 см, температуры наружной и внутренней поверхностей стенки соответственно t₁= 20^oC, t₂= –20^oC. Определить стоимость потерь при цене 1кВт·час энергии 1 руб.

Решение. По формуле (3.86) определяем потери тепла через кирпичную стенку

,

потери тепла через деревянную стенку

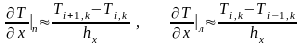
Один кВт·час тепловой энергии составляет 1·3600=3600 Дж, следовательно, стоимость потерь через кирпичную стенку составляет 62500/3600=17,4 руб, а через деревянную стенку – 22200/3600=6,2 руб, что почти в 3 раза меньше.