
- •Лекция 5 Постановка краевой задачи теплопроводности
- •Дифференциальное уравнение теплопроводности
- •Уравнение теплопроводности при неоднородных свойствах
- •Уравнение теплопроводности для анизотропных сред
- •Уравнение теплопроводности для высокоскоростных процессов
- •Краевые условия
- •3.7. Безразмерная формулировка краевой задачи теплопроводности
- •3.8. Стационарная теплопроводность плоского слоя
- •Метод регулярного теплового режима расчета нагрева (охлаждения) тел
- •3.10. Теплопроводность при плавлении-затвердевании металла
- •3.11. Метод сквозного счета в задачах теплопроводности при структурных и фазовых переходах
- •3.12. Приближенный учет конвекции жидкого ядра кристаллизующегося слитка
Лекция 5 Постановка краевой задачи теплопроводности
Вопросы
Дифференциальное уравнение теплопроводности
Краевые условия
Стационарная теплопроводность плоского слоя
Безразмерная формулировка краевой задачи теплопроводности
Метод регулярного теплового режима расчета нагрева (охлаждения) тел
Теплопроводность при плавлении-затвердевании металла
Метод сквозного счета в задачах теплопроводности при структурных и фазовых переходах
Приближенный учет конвекции жидкого ядра кристаллизующегося слитка
Краевая задача теплопроводности включает дифференциальное уравнение теплопроводности, имеющее единственное решение при заданном начальном распределении температуры и условиях теплообмена на границах расчетной области.
Дифференциальное уравнение теплопроводности
Дифференциальное уравнение теплопроводности является частным случаем уравнения переноса энергии и связывает производные температуры по координате и времени
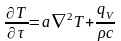 .
(3.50)
.
(3.50)
Физический
смысл уравнения: тепло
от внутренних источников заданной
мощности qV,
а также тепло, подведенное к элементарному
объему от соседних теплопроводностью
 ,
идет на увеличение внутренней энергии
этого элементарного объема
,
идет на увеличение внутренней энергии
этого элементарного объема
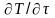 .
.
Коэффициент пропорциональности а называется коэффициентом температуропроводности
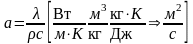 . (3.51)
. (3.51)
Он характеризует скорость изменения температуры и является мерой теплоинерционных свойств тела. При прочих равных условиях выравнивание температур во всех точках пространства будет происходить быстрее в том теле, которое обладает большим коэффициентом температуропроводности.
Частные случаи уравнения теплопроводности:
qV =0

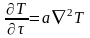 – уравнение Фурье,
описывает нестационарную теплопроводность
в теле без источников (стоков) тепла;
– уравнение Фурье,
описывает нестационарную теплопроводность
в теле без источников (стоков) тепла;
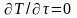
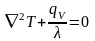 – уравнение
Пуассона,
описывает стационарную теплопроводность
в теле с источниками (стоками) тепла;
– уравнение
Пуассона,
описывает стационарную теплопроводность
в теле с источниками (стоками) тепла;qV =0,
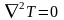 – уравнение Лапласа,
описывает стационарную теплопроводность
в теле без источников (стоков) тепла.
– уравнение Лапласа,
описывает стационарную теплопроводность
в теле без источников (стоков) тепла.
Уравнение теплопроводности при неоднородных свойствах
Дифференциальное уравнение теплопроводности (3.50) было получено в предположении постоянной теплопроводности (λ=const), в действительности теплопроводность зависит от температуры, λ=λ(Т), поэтому при выводе уравнения теплопроводности нельзя выносить плотность теплового потока за знак дивергенции. В этом случае уравнение теплопроводности становится нелинейным, так как входящий в него коэффициент λ зависит от распределения температуры
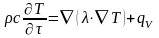 (3.52)
(3.52)
Нелинейное уравнение теплопроводности (3.52) можно привести формально к виду линейного уравнения (3.50), для этого преобразуем диффузионный член уравнения
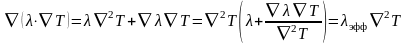 ,
,
С введением понятий эффективных коэффициентов теплопроводности
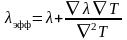 ,
(3.53)
,
(3.53)
и температуропроводности
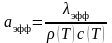 (3.54)
(3.54)
дифференциальное уравнение теплопроводности принимает стандартный вид
 ,
(3.55)
,
(3.55)
удобный при численной реализации на компьютере.
