§3. Формула Грина

1.Формула Грина

Рассмотрим область типа A ( см. рис. ) D={(x,y):y₁(x) y  y₂(x), x[a,b]}, где y₁(x) y₂(x), две непрерывные функции на отрезке [a,b].

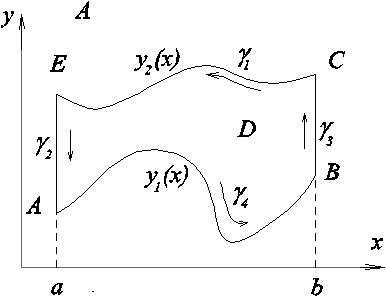
Границу этой области с положительным направлением обхода обозначим  . Пусть в области D задана функция P(x,y), непрерывная там вместе со своей частной производной . Тогда справедлива формула

= -.(1)

Доказательство. ===-=-=.

Здесь используются равенства =0,=0, следующие непосредственно из определения интеграла. Аналогично, можно показать, что для области типаB (см. рис. )

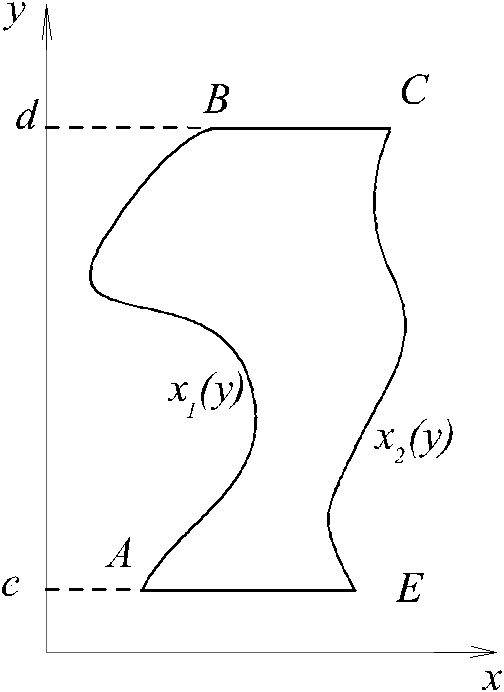
справедлива формула

= .(2)

Если область является одновременно областью и типа A и типа B ,

то из (1), (2) для поля =(P,Q) получается формула

(3)

Формулы (1), (2), (3) называются формулами Грина.

Замечание. Формула (3) верна и для областей более общего вида. В частности, если область можно разбить непрерывными кривыми на конечное число областей, для каждой из которых формула (3) справедлива, то эта формула будет верна и для всей области.

Для области, показанной на рисунке, можно сделать разрез, как показано на рисунке.

Область разбивается на две области D₁ , D₂ , для которых справедлива формула Грина.

Введем обозначения D₁ =₁+₂ , D₂ =₃+₄= , тогда D =₁+₄ . При этом +=0. Тогда

=+=+=+++=+=.

Пример 1. (4307) Вычислить . КонтурC оринтирован положительно. Рассмотреть два случая: контур не содержит начало координат, контур содержит начало координат.

Обозначим через D область, ограниченную контуром C. Вычислим частные производные

==,

==,

Таким образом, в первом случае ==0.

Во втором случае формула Грина не может быть использована, так как поле (P,Q) имеет особенность в начале координат, которая попадает в область интегрирования. Выберем круг с центром в начале координат и достаточно малого радиуса r так, чтобы он содержался в области D. Границу этого круга, ориентированную положительно, обозначим C_r . Произведем два разреза кусочно-гладкими кривыми, соединяющие какие либо две точки границы контура C с какими либо точками окружности C_r . На рисунки в качестве разрезов выбраны отрезки прямой и показаны обозначения для некоторых кривых, образовавшихся в результате этих разрезов. Отметим, что

C=C₁+C₈ , =C₃+C₆ , C₂=, C₄=.

Внутри контуров C₁+ C₂+ C₃+ C₄ и C₅+ C₆+ C₇+ C₈ особенностей нет и, как было доказано, с Контур =C₁+ C₂+ C₃+ C₄+ C₅+ C₆+ C₇+ C₈ не содержит внутри себя ни каких особенностей векторного поля (P,Q) и, поэтому к нему применима формула Грина

0====.

Таким образом. ==.

Пример 2. (4303) Вычислить , гдеAmB – верхняя полуокружность x²+y²=ax , начало - A(a,0), конец – B(0,0).

, . .

==.

==.

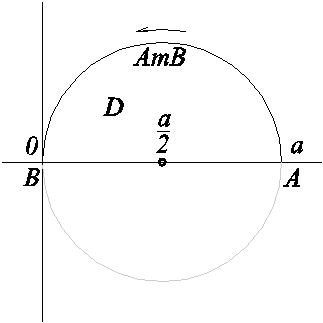
AB- имеет параметризацию .

Тогда

=+=.

Пример 3. (4304) Вычислить , где функцияf(y) – непрерывно дифферинцированная на проекции кривой AmB функция (проекция на ось Oy), AmB – кривая, соединяющая точки A, B, ограничивающая вместе в отрезком AB область D.

, . .

=.

=mD= mD.

AB- имеет параметризацию , A=(x₀,y₀),B=(x₁,y₁), x=x₁ - x₀ , y=y₁ - y₀ .

Тогда

=

=

-==.

= mD+.

2.Использование формулы Грина для вычисления площадей.

Если в качестве функций P, Q взять функции, для которых , то получится формула для вычисления площади области, ограниченной кривой  .

.

Можно предложить три варианта таких функций

1. Q=x, P=0 и тогда .

2. Q=0, P=-y и тогда .

3. Q=,P=и тогда .

Пример 1. Вычислить площадь астроиды

=====ab.

Пример 2. Вычислить площадь лемнискаты (x²+y²)²=a²(x²-y²).

В полярных координатах .

Параметризация правой ветви .

=+===.

3. Условия независимости интеграла второго рода от пути интегрирования.

Определение. Область называется односвязной, если ее граница представляет собой связное множество. Область называется n-связной, если ее граница распадается на n- связных множеств.

Замечание. Формула Грина верна и для многосвязных областей.

Например, для области, показанной на рисунке произведены разрезы, соедеиняющие обе связные компоненты границы между собой.

Можно выписать цепочку равенств

=+=+=+++++++=+++=+=.

Замкнутая кривая называется контуром. Криволинейный интеграл второго рода в этом случае иногда обозначается .

До конца этого пункта будем считать, что область D - открытое и односвязное множество, а функции P(x,y), Q(x,y) непрерывны в замыкании D вместе со своими производными ,.

Лемма. Для того, чтобы интеграл

(4)

( A, B – любые точки из D ) не зависел от пути интегрирования ( а только от начальной и конечной точек A, B ) необходимо и достаточно, чтобы по любой замкнутой кривой (по любому контуру) лежащей в D интеграл (4) был равен нулю

=0.

Интеграл называется циркуляцией векторного поляV=(P,Q).

Доказательство (необходимость). Пусть (4) не зависит от пути интегрирования. Рассмотрим произвольный контур C, лежащий в области D и выберем две произвольные точки A, B на этом контуре. Тогда кривую C можно представить, как объединение двух кривых ₂ (из A в B, как на рисунке ) и ₁ (тоже из A в B, но по другой ветви ), C=+₂ .

По условию =, кроме того=, поэтому=+=-=0. Для доказательства достаточности рассмотрим две точкиA, B в области D и два пути AB=₂ , AB=₁ соединяющие эти две точки. Рассмотрим контур C=+₂ . По условию =0 , откуда, с учетом соотношения=+=-, следует требуемое равенство=. В этом доказательстве предполагается, что кривые₂ ,₁ не пересекаются. Самостоятельно доказать это утверждение для случая, показанного на рисунке ниже

Теорема 1. Для того, чтобы криволинейный интеграл (4) не зависел от пути интегрирования в D, необходимо и достаточно чтобы

в области D. (5)

Достаточность. Если (5) выполнено, то формуле Грина для любого контура C будет

=0,

откуда по лемме следует требуемое утверждение.

Необходимость. По лемме для любого контура = 0. Тогда по формуле Грина для области , ограниченной этим контуром =0. По теореме о среднем 0== или ==0.Переходя к пределу, стягивая контур к точке, получим, что в этой точке .

Теорема 2. Для того, чтобы криволинейный интеграл (4) не зависел от пути интегрирования в D, необходимо и достаточно чтобы подинтегральное выражение Pdx+Qdy являлось полным дифференциалом некоторой непрерывно дифференцируемой функции u(x,y) в области D

du = Pdx+Qdy (6)

Достаточность. Пусть (6) выполнено, тогда ,,и можно сослаться на теорему 1.

Необходимость. Пусть интеграл не зависит от пути интегрирования. Фиксируем некоторую точку A₀ в области D и определим функцию

u(A) = u(x,y)=.

В этом случае

, [x,x+x] ([x+x,x]). Таким образом, существует производная =P. Аналогично, проверяется, что =Q. При сделанных предположениях функция u оказывается непрерывно - дифференцируемой и du = Pdx+Qdy.

Замечание 1. Условие односвязности области D в сформулированных теоремах существенно.

Ранее был рассмотрен пример с интегралом , где==. В случае, когда область содержит начало координат, полученная область является двусвязной, в частности, интегралы по контурам, содержащим начало координат не равны нулю.

Замечание 2. При доказательстве теоремы 2 была построена функция u(x,y)= . Эта функция определяется с точностью до аддитивной постоянной и называется потенциалом (скалярным) векторного поля (P,Q).

Пример. Решить дифференциальное уравнение .

Для поля = будет выполнено .

В этом случае для функции u(x,y)= выполняется равенство du = Pdx+Qdy и, следовательно, u(x,y)=Const есть решение исходного дифференциального уравнения. Найдем функцию u. Пусть M =(x, y) текущая точка области M₀=(0,0). В качестве кривой, соединяющей точки M₀ и M , выберем отрезок

 : ,

==+=+=+=.