Глава 2. Кратные интегралы. Продолжение

§1. Тройные и n-кратные интегралы

1.Определение тройного и n-кратного интеграла

Пусть D кубируема, ее площадь будем обозначать D , функция f(M)=f(x,y,z) определена и ограничена в области D. Предположим, что D разбита поверхностями на кубируемые подобласти D_k (совокупность {D_k} называется разбиением области D). В каждой из подобластей D_k выберем точку M_k=(_k,_k,_k)D_k. Полученный набор точек обозначим  ={M_k}. Интегральной суммой для набора f, разбиения  , набора промежуточных точек  называется выражение

(1)

Суммирование производится по всем областям разбиения. Величина ()=dD_k называется характеристикой разбиения  . Здесь – диаметр множества D_k .

Условие M_kD_k, для всех k мы будем обозначать .

Определение. Предел интегральных сумм (f,, ) при ()0 (если он существует и не зависит от выбора разбиений и промежуточных точек ) называется тройным интегралом от функции f на D и обозначается

=.

Можно использовать обозначение =( вместо M можно использовать любую подходящую букву, например ).

Более точно это определение выглядит следующим образом:

J>0>0:(()<, )|(f,, ) - J|<.

Понятие длины, площади, объема распространяется и на области n- мерного евклидова пространства. В этом случае говорят об измеримости множества D n- мерного пространства и о его мере D. Для измеримой области D и определенной на ней функции f(x)=f(x₁,x₂,…,x_n) рассматривается разбиение этой области на измеримые множества {D_k}. В каждой из подобластей выбираются промежуточные точки ^k=()D_k. Полученный набор точек обозначим  ={^k}. Интегральной суммой для набора f,  ,  называется выражение

(1)

Суммирование производится по всем областям разбиения. Величина ()=dD_k , где максимум берется по всем множествам разбиения, называется характеристикой разбиения  . Как и раньше, – диаметр множества D_k , где точная верхняя грань берется по всевозможным точкам x=(x₁,x₂,…,x_n), y=(y₁,y₂,…,y_n) из D_k .

Определение. Предел интегральных сумм (f,, ) при ()0 (если он существует и не зависит от выбора разбиений и промежуточных точек ) называется интегралом от функции f на D и обозначается

=.

Для n-кратных интегралов имеют места свойства, аналогичные свойствам, сформулированным для двойных интегралов. Перечислим некоторые из этих свойств.

1)

2. Если f и g интегрируемы на D, то f + g также интегрируема и

(f(x) + g(x))dx = f(x)dx + g(x)dx.

2. Если f интегрируема на D , то cf(x) также интегрируема и

=c.

2. Если f интегрируема на D , то |f| также интегрируема и

| | £.

2. Если f и g интегрируемы на D и f £ g на D , то

£ .

6) Если m  f(x)  M на D, то  c[m,M] :

= c D.

Следствие. Если f непрерывна на связном компакте D, то D:

= f()D.

7) Непрерывная на компакте функция интегрируема на этом компакте.

8) Если D = 0, то для любой ограниченной функции f будет выполнено

f(x) dx=0.

2. Сведение тройного интеграла к повторному для прямоугольного параллелепипеда

Пусть V – прямоугольный параллелепипед [a,b] [c,d]  [g,h] и функция f(x,y,z) определена на V. Обозначим прямоугольник [c,d]  [g,h] через D.

Теорема. Если существует и для любогоx[a,b] существует , то существует интеграли имеет место равенство

=.

(здесь и в дальнейшем используются обозначения=)

Доказательство. Рассмотрим разбиение  области V :

={a=x₀<…<x_n=b;c=y₀<…<y_m=d;g=z₀<…<z_l=h}.

Полученные подобласти обозначим V_ijk=[x_i,x_i+1][y_j,y_j+1][z_k,z_k+1],i=0,…,n-1, j=0,…,m-1, z=0,…,l-1. Кроме того, будем использовать обозначения X=(x,y,z)

m_ijk=, M_ijk=. Тогда для XV_ijk справедливы неравенства m_ijk f(X)  M_ijk .

Для набора промежуточных точек { _i },  _i  [x_i,x_i+1] будет выполнено

m_ijk y_j z_k   M_ijk y_j z_k,

m_ijk y_j z_k   M_ijk y_j z_k,

Домножая последние неравенства на x_i и суммируя, получим

m_ijk x_i y_j z_k   M_ijk x_i y_j z_k .

Средняя сумма является интегральной суммой для интеграла ,крайние суммы являются суммами Дарбу для интеграла ,откуда и следует требуемое утверждение.

Аналогичные теоремы можно доказать для других порядков интегрирования. Таким образом, при выполнении соответствующих условий получаются равенства вида

=,

=,

=.

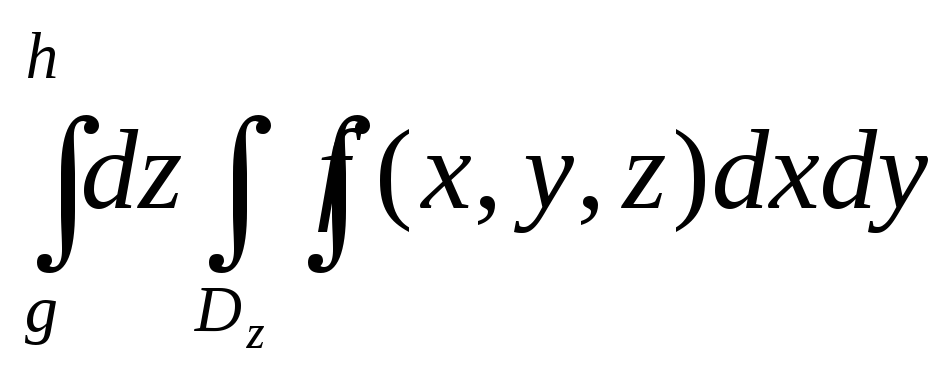Через D_x , D_y , D_z обозначены проекции области V на координатные плоскости x=0, y=0, z=0 , соответственно.

В свою очередь внутренние двойные интегралы можно представить в виде повторных. Для первого из написанных соотношений это будет выглядеть следующим образом

=,

=.

(используются обозначения=)

Теперь можно собирать внешние повторные интегралы в двойные, в результате получаться три равенства

=,

=,

=,

Здесь D_xy =D_z =[a,b] [c,d], D_zx=D_y =[g,h]  [a,b] , D_yz =D_x = [c,d]  [g,h].

3. Сведение тройного интеграла к повторному интегралу для областей общего вида

Пусть V – область, расположенная между плоскостями x=a, x=b, L_x – плоскость параллельная координатной плоскости Oyz, проходящая через точку x.Для x  [a,b] обозначим через D_x сечение V L_x . Будем предполагать, что D_x квадрируема для всех x  [a,b]. При этих предположениях справедлива

Теорема. Если существует и дляx[a,b] существует I(x)=то существует ии

=.

Доказательство. Обозначим через R=[a,b] [c,d]  [g,h] прямоугольный параллелепипед, содержащий область V и определим на R функцию

f^*(M)=.

Тогда

=, R_x= [c,d] [g,h].

Для левого и правого интегралов справедливы равенства

=+=.

==.

Замечание. Сечение D_x = V L_x может быть задано в виде

D_x = {(y,z): y₁(x)  y  y₂(x) , z₁(x,y)  z  z₂(x,y)}.

В этом случае пределы интегрирования в тройном интеграле можно расставить следующим образом ==.

D – представляет собой проекцию V на плоскость z=0. Эту область можно также описать в виде

D = {(x,y):a  x  b, y₁(x)  y  y₂(x)}. Расставляя переменные x,y,z в другом порядке можно получить другие аналогичные формулы представления тройного интеграла через повторные.

4. Замена переменных в тройном и n-кратном интеграле

Пусть задано взаимно-однозначное, непрерывно - дифференцируемое отображение с якобианом, отличным от нуля

, (, ,  ) 

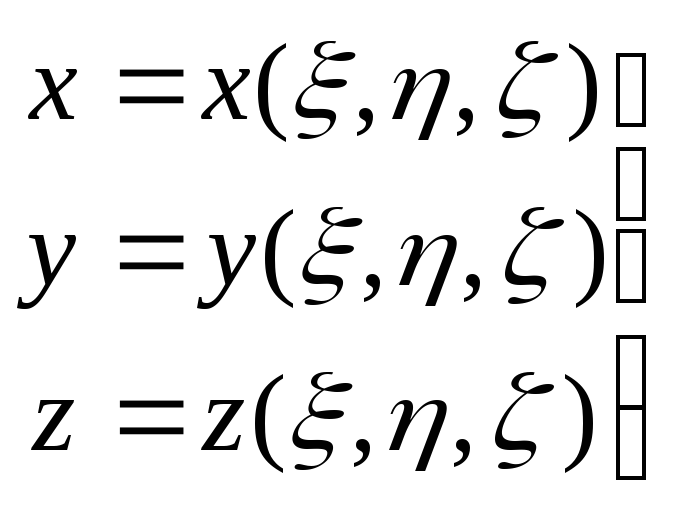из  в V, где области  и V кубируемы. Тогда для объема области V справедлива формула

 V = (4).

Из этой формулы и теоремы о среднем следует, что

= V = = .

Откуда следует, что в любой точке области M₀=(₀ ,₀ ,₀ )

=.

Теорема ( о замене переменных ). Если f интегрируема в V, то

= .

Доказательство. Интегралы справа и слева существуют. Интегрируемость функции F(,,)=f[x(,,),y(,,),z(,,)] на  доказывается так же, как и в случае двойного интеграла. Выберем какое-либо разбиение {_j} области  и обозначим через {V_j} соответствующее разбиение области V. Согласно формуле (4)

 V_j = = _j.

Полученные таким образом точки M_j = (_j , _j , _j ) будем рассматривать как промежуточные точки для интегральных сумм функции F(,,) и разбиения {_j}, а соответствующие точки P_j = (x_j , y_j , z_j ) для интегральных сумм функции f(x,y,z) и разбиения {V_j}. В этом случае

.

Из этого равенства следует требуемое утверждение.

Пример 1. Цилиндрические координаты

, x²+y²=z², 0  z  1

, .

В этом случае D = {(r,,h): 0    2 , 0  r  z ,  z[0,1]} .

== ===.

Пример 2. Сферические координаты

A=, x²+y²+z²  1, 0  x , 0  y , 0  z .

, ==

=-sin (²sin cos sin²+²sin cos cos²)-cos( cos² sin²+ cos² cos²) =

=-sin ²sin cos -cos  cos² =-²cos  .

A===.

Пример 3. В интеграле расставить пределы интегрирования в порядке dxdzdy и dzdxdy.

Пример 4. Заменить тройной интегрлал однократным

=+=+=+

5. Замена переменных в общем случае

Рассмотрим регулярное отображение

( кратко x=x(u) )

из области  в область V. При измеримости областей  , V справедлива формула замены переменных

=,

существование интегралов предполагается.