§6. Вычисление двойных интегралов

1.Интегрирование по прямоугольнику.

Рассмотрим прямоугольник D=[a,b][c,d]={(x,y)a  x  b, c  y  d }.

Теорема. Если f интегрируема на D и для x существует =J(x), то существует и и выполнено равенство

==.

Доказательство. Для заданных разбиений _x={a=x₀<…<x_n=b}, _y={c=y₀<…<y_m=d} рассмотрим разбиение  ={ D_ij} области D, где D_ij=[x_i,x_i+1] [y_j, y_j+1],

введем обозначения m_ij=, M_ij=, ={(_i, _j)}, _i[x_i, x_i+1], _j[y_j, y_j+1], x_i=x_i+1 – x_i, y_j=y_j+1-y_j . Тогда будут выполнены неравенства

m_ij  f(x,y)  M_ij для (x,y)D_ij (1)

m_ij y_j   M_ij y_j (2)

 (3)

Умножая неравенства (3) на x_i и суммируя, получим

m_ij x_i y_j  x_i  M_ij x_i y_j .

При ()0 суммы слева и справа (суммы Дарбу) будут сходиться к интегралу , средняя сумма представляет собой интегральную сумму для интеграла , откуда и следует требуемое утверждение.

Замечание. Аналогичное утверждение получается, если поменять местами x,y.

Если f интегрируема на D и для y существует =I(y), то существует и и выполнено равенство

==.

Интегралы , называются повторными.

Следствие (перемена порядка интегрирования). Если f интегрируема на D и для y существует =I(y), x существует =J(x), то существуют, 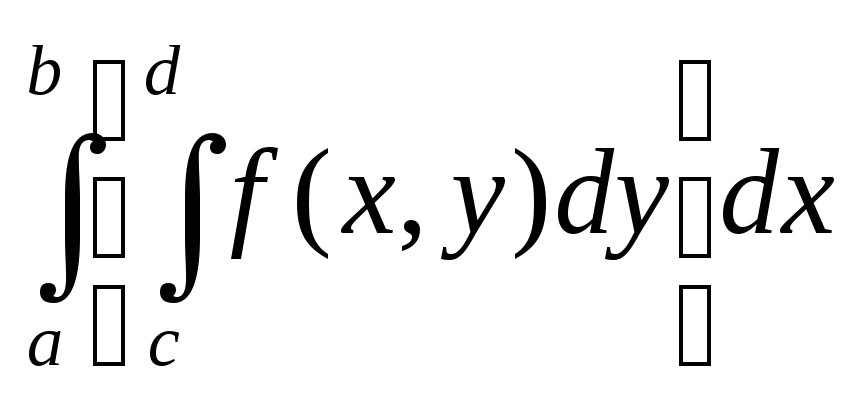и выполнено равенство

==.

2. Интегрирование по области, представляющей собой криволинейную трапецию

Рассмотрим область D={(x,y): y₁(x)  y  y₂(x), x[a,b]}, где y₁(x), y₂(x) – непрерывные функции на [a,b]. Области такого вида будем называть областями типа A. Области вида D={(x,y): x₁(y)  x  x₂(y),y[c,d]}, где x₁(y), x₂(y) – непрерывные функции на [c,d] называются областями типа B .

Теорема. Если для области типа A существуют и дляx[a,b] существует, то существует и

=.

Доказательство. Пусть D={(x,y): y₁(x)  y  y₂(x), x[a,b]}, где y₁(x), y₂(x) – непрерывные функции на [a,b]. Рассмотрим функцию

f ^*(x,y) = ,

где R=[A,B][C,E] прямоугольник, содержащий область D. Для функции f ^* выполнены условия предыдущей теоремы, поэтому

=.

Далее = =. По теореме 3 из параграфа 4 выполнено равенство= откуда и следует требуемое равенство. Аналогично доказывается

Теорема. Если для области типа B существуют иy[c,d] существует, то существует и

=.

Примеры: Расставить пределы интегрирования в интегралев том и другом порядке.

1. D={(x,y):0  x  1, x2 y 1+(x-1)2}	2.D={(x,y):0  x  1, x2-1 y cos().

§7. Замена переменных в двойном интеграле

1. Отображение плоских областей. Криволинейные координаты.

Рассмотрим два экземпляра плоскости, плоскость переменных x, y и область D в этой плоскости, плоскость переменных ,  и область  в этой плоскости

Пусть имеется взаимно однозначное отображение области D на 

(1),

(2).

Будем предполагать, что отображения (1), (2) непрерывно дифференцируемы и якобианы этих отображений

0, 0.

Отметим, что

=1.

В области  рассмотрим некоторую кусочно-гладкую кривую

t[,].

Ее образ в D имеет параметризацию

t[,]

и будет также кусочно-гладкой кривой. Действительно,

(3).

Если (,)(0,0), то и (x,y)(0,0). Если предположить противное, то система (3) с не вырожденной матрицей коэффициентов должна будет иметь только тривиальное решение, что противоречит условию (,)(0,0).

Определение. Кривая, составленная из точек области D вида

или

называется координатной линией

Неявное задание этой линии имеет вид (x,y)=₀ (соответственно (x,y)=₀).

Определение. Числа ₀ , ₀ из области  плоскости ( , ) определяющие положение точки (x₀ ,y₀) из области D плоскости (x ,y) называются криволинейными координатами точки (x₀ ,y₀). Наоборот, на (x₀ ,y₀) можно смотреть, как на криволинейные координаты точки (₀ , ₀).

Фиксируя значения  или  на плоскости ( ,) можно получить два семейства координатных линий. В области D появляется криволинейная координатная сетка. При сделанных предположениях две линии одного семейства не пересекаются между собой и, через любую точку области D проходит по одной линии из каждого семейства

2. Изменение площади при отображениях.

Рассмотрим отображение

и его обратное

удовлетворяющее условиям предыдущего пункта и разбиение области D линиями, порожденными линиями =const, =const плоскости , 

Рассмотрим прямоугольник ,  +, , ,  + в плоскости ,  и его образ в плоскости x, y.

Обозначим для краткости x=x(,), y=y(,), тогда

x( + ,)= x + + o(), y( + ,)= y + + o(),

x( , +)= x + + o(), y( , +)= y + + o(),

x( + ,  +)= x + + + o(), y( + ,  +)= y + + + o().

Для вычисления площади фигуры с вершинами

A(x,y), B(x( + ,), y( + ,)), C(x( + ,  +), y( + ,  +)), E( x( , +), y( , +))

рассмотрим параллелограмм A=A, B, C, E с координатами вершин

A=A=(x,y), B=( x +, y + ), C=( x + +, y + + ),

E=( x +, y + ) .

Этот параллелограмм построен на векторах AB, AE,

a=AB = ( ,), b=AE = ( , ). Поэтому его площадь равна

 [a,b]==.

Вершины A,A, B,B, C,C, E,E отличаются на o(). Можно показать, что в этом случае площади будут отличаться на o(²)

(A,B,C,E)= + o(²).

Отсюда, в свою очередь, следует, что площадь области D будет равна

D== (4).

Докажем последнее равенство для случая, когда область  представляет собой квадрат [,][,]

Разобьем  на равные части линиями =_i , =_j .

В этом случае _i=_i+1 - _i = ( - )/n , _j=_j+1 - _j = ( - )/n , ==( - )/n, D=.

Можно показать, что последнее слагаемое является бесконечно малой при n , откуда и следует равенство (4).

Замечание. Выражение dxdy иногда называют элементом площади в плоскости x,y, а выражение dd - элементом площади в плоскости , . Равенство (4) позволяет говорить, что модуль якобиана является коэффициентом искажения площади при данном отображении

dxdy =dd.

Из равенства D=следует, что в любой точке области M₀=(₀ ,₀ ,₀ )

=.

3.Примеры отображений.

Экспонента

, =[-3,1][0,]

Функция Жуковского

,=( в полярных кординатах) [0,][0.25,0.9]

Дробно линейное отображение

,= [0.25,1][0,1]

4. Замена переменных в двойном интеграле.

Рассмотрим отображение

и его обратное ,

непрерывно дифференцируемое и имеющее отличный от нуля якобиан в области D.

Лемма. Если функция f(x, y) интегрируема на D, то функция F(, )=f(x(, ),y(, )) интегрируема на  .

Доказательство. Любое разбиение области D порождает разбиение области  и наоборот. Таким образом связанные между собой разбиения, будем обозначать _D={D_k} , _={_k}. Здесь D_k и _k – подобласти, переходящие друг в друга при заданном отображении .

Для разбиений _D={D_k} , _={_k} можно выписать соотношение между колебаниями функций

_k(F)== =_k(f).

Далее =.

Поэтому

S(F, _)-s(F, _)== С=C(S(f,_D)-s(f, _D)).

Откуда и следует интегрируемость функции F(, ) на .

Теорема. Пусть функция f интегрируема в D, тогда

= .

Доказательство. Согласно доказанной лемме интеграл справа существует. Выберем некоторое разбиение области  на подобласти _i и соответствующее ему разбиение области D на множества D_i. Тогда по теореме о среднем для каждого i будет существовать точка (_i , _i ), для которой

D_i = ==.

Для этих точек (_j,_j ) и соответствующих им точек (x_j,y_j ) можно выписать интегральные суммы

.

При переходе к пределу при измельчении разбиения левая и правая части этого равенства будут сходиться к интегралам

, ,

соответственно.

Пример 1. Рассмотреть область D={[,],r[r₁,r₂]} и сделать замену в интеграле , используя полярные координаты.

Пример 2. Сделать замену переменных u=x+y, v=y – x в интеграле для областиD={|x|+|y| 1}.

Пример 3 (3959). Сделать замену переменных x=u cos⁴v, y= u sin⁴v в интеграле для областиD, ограниченной кривыми x=0, y=0, .

Пример 4. Является ли конечной площадь области, заключенной между биссектрисой 2-4 –го координатных углов и кривой (x³+y³)²=x²+y².

Перейдем к полярным координатам

r⁶(cos³+sin³)²=r²,

D=========. Последний интеграл расходится.