§2. Выражение операций теории поля в криволинейных координатах

1. Введение.

В дальнейшем будут использоваться следующие обозначения. С исходной декартовой системой координат xyz ( или x₁x₂x₃ ) связана криволинейная система координат x¹x²x³ отображением

или

Это отображение предполагается невырожденным, непрерывно дифференцируемым и имеющим отличный от нуля якобиан. Обратное отображение имеет вид

.

Согласно правилам дифференцирования сложных функций справедливы соотношения или в матричном виде

= .

Здесь использованы следующие обозначения для матриц Якоби и ковариантных, контравариантных векторов:

,

звездочкой внизу обозначены ковариантные координаты.

Таким образом, вектора являются сопряженными к

r_i = ,т. е. r^j = .

В дальнейшем будут использоваться следующие обозначения:

u_k=,

2. Выражение градиента в криволинейных координатах

Для скалярного поля u градиент в декартовой системе координат равен

grad u = . По формуле дифференцирования сложной функции

=(grad u , r_i ) = u_i . По формулам Гиббса

grad u = (grad u , r_i ) rⁱ =u_i rⁱ .

Откуда для ортогональной системы координат

grad u = u_i rⁱ = u_i = u_i .

2. Выражение дивергенции в криволинейных координатах

Обозначим V = Pi +Qj + Rk , V_i == , тогда

div V = =++=

= +

+ +

+ = (V₁,r¹)+(V₂,r²)+(V₃,r³) = (V_k,r^k) =

=.

В ряде случаев приходится рассматривать разложение исходного поля V по базису e_k : V = e_k A^k . В этом случае предварительно вычисляют производные V_k и полученные выражения подставляют в формулу для данной операции, например, в формулу div V =. Можно показать, что

div V = .

4. Выражение ротора в криволинейных координатах

V = Pi +Qj + Rk , V_i ==,

rot V = ==

=

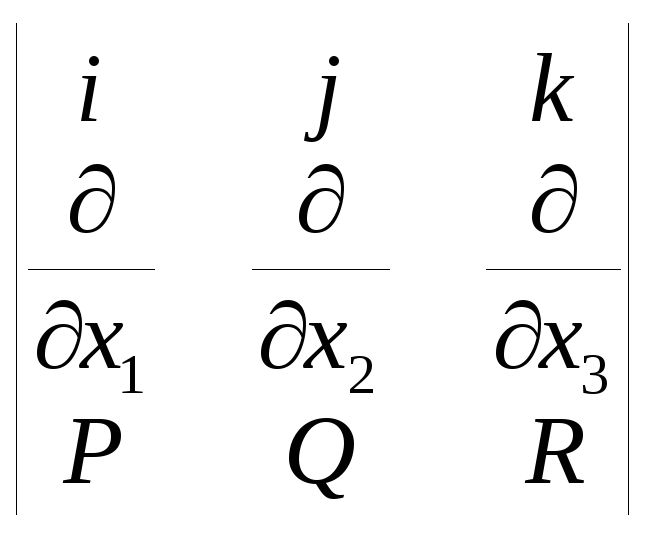==-[ V_k , r^k]= [r_k , V_k]= [e_k , V_k].

2. Выражение оператора Лапласа в криволинейных координатах

grad u = ,, A^k = , div grad u = (V_k , r^k). Тогда из формулы div V = получим u = div grad u = .

§3. Выражение операций теории поля в цилиндрических координатах

1. Цилиндрические координаты (r, , h) = (x¹,x²,x³).

x = r cos 

y = r sin 

z = h

r1 = (cos  , sin  , 0), H1 = |r1| = 1, r2 = (-r sin  ,r cos  , 0), H2 = |r2| = r, r3 = ( 0 , 0 , 1), H3 = 1.

e₁ = e_r = (cos  , sin  , 0) ,

e₂ = e_ = (-sin  ,cos  , 0) ,

e₃ = e_h = ( 0 , 0 , 1) .

Базис e_r , e_ , e_z – ортонормированный.

,

, , ,

.

2. Выражение градиента в цилиндрических координатах

grad u = u_i rⁱ = u_i = u_i .

grad u =r₁ +r₂ + r₃ = e_r +e_ + e_h .

2. Выражение дивергенции в цилиндрических координатах

V = Pi +Qj + Rk , V_i ==, V₁ = , V₂ = , V₃ = .

Если V = e_kA^k , то

V₁ = V_r = ( e_kA^k) = e_k A^k + A^ke_k = e_k A^k .

V₂ = V_ = ( e_kA^k) = e_k A^k +A^k = e_k + A¹e₂ - A²e₁ .

V₃ = V_h = ( e_kA^k) = e_k + A^k = e_k .

Отсюда следует

div V = (V_k,r^k) = = =_.

4. Выражение ротора в цилиндрических координатах

[e₁, e₂]=e₃ , [e₃, e₁]=e₂ , [e₂, e₃]=e₁ ,

[e₁, V₁] = [e₁, e₂] + [e₁, e₃] = e₃ - e₂,

[e₂, V₂] ==,

[e₃, V₃] = [e₃, e₁] + [e₃, e₂] = e₂ - e₁ ,

rot V =++.

5. Выражение оператора Лапласа в цилиндрических координатах

H = H₁ H₂ H₃ = r,

u = div grad u = = =.

§4. Выражение операций теории поля в сферических координатах

1. Сферические координаты (, , ) = (x¹,x²,x³).

x =  cos  cos 

y =  cos  sin 

z =  sin 

r1 = (cos  cos  , cos  sin  , sin ), H1 = |r1| = 1, r2 = (- cos  sin  ,  cos  cos  , 0), H2 = |r2| =  cos , r3 = (- sin  cos  , - sin  sin  ,  cos ), H3 = .

e₁ = e_ = (cos  cos  , cos  sin  , sin ),

e₂ = e_ = (- sin  , cos  , 0),

e₃ = e_ = (- sin  cos  , - sin  sin  , cos ).

Базис e_ , e_ , e_ – ортонормированный.

,

= cos  e₂ , = - cos e₁ + sin  e₃ , = - sin e₂ ,

= e₃ , = 0 , = - e₁ .

2. Выражение градиента в сферических координатах

3. grad u = u_i rⁱ = u_i = u_i .

grad u =r₁ +r₂ + r₃ = e_ +e_ +e_

2. Выражение дивергенции в сферических координатах

Пусть V =e_k A^k ,

V₁ = V_ = (e_k A^k) = e_k + A^k= e_k .

V₂ = V_ = ( e_kA^k) = e_k + A^k =

= e_k – A² cos  e₁+(cos A¹ - A³sin  ) e₂ + A² sin  e₃ = .

V₃ = V_h = ( e_kA^k) = e_k + A^k =.

Отсюда следует

div V = (V_k,r^k) = = (V₁,e₁) (V₂,e₂) + (V₃,e₃) = + +=+.

4. Выражение ротора в сферических координатах

[e₁, e₂]=e₃ , [e₃, e₁]=e₂ , [e₂, e₃]=e₁ ,

[e₁, V₁] = [e₁, e₂] + [e₁, e₃] = e₃ - e₂,

[e₂, V₂] ==

,

[e₃, V₃] = [e₃, e₁] + [e₃, e₂] [e₃, e₁] =

= e₂ e₁ ,

rot V = e₃ - e₂ ++ e₂ e₁ =

=++.

5. Выражение оператора Лапласа в сферических координатах

H₁ = 1, H₂ =  cos , H₃ = ,

u = div grad u = = =.