§2. Поверхностные интегралы 2-го рода

1.Определение стороны поверхности

Для поверхностей, которые нам встречались до сих пор можно ввести понятие стороны поверхности. Такие поверхности характеризуются, как двухсторонние поверхности. Их можно выкрасить в два цвета так, что один цвет не будет переходить в другой. Аналитически сторону поверхности можно определить, как множество всех единичных нормалей к поверхности таких, что любые две нормали данной стороны получаются одна из другой непрерывным движением по поверхности вдоль некоторой непрерывной кривой, лежащей на этой поверхности. Существуют поверхности, не обладающие подобным свойством. Такие поверхности называются односторонними.

Примерами односторонних поверхностей могут служить лист Мёбиуса и «бутылка» Клейна.

Можно дать следующее определение односторонней и двухсторонней поверхностей. Поверхность называется двухсторонней, если выполнено следующее свойство: для произвольной точки поверхности при движении по любому замкнутому пути, лежащем на поверхности и выходящем из этой точки, мы возвращаемся в эту точку с тем же направлением нормали.

Если же существует хотя бы один замкнутый путь, двигаясь по которому мы вернемся в исходную точку с противоположным направлением нормали, то такую поверхность называют односторонней. Предполагается, что при движении вдоль пути, нормаль изменяется непрерывно. Для листа Мебиуса такой линией, например, является продольная пунктирная линия. Если произвести разрез по этой линии, то поверхность не распадется на две части, как это может показаться на первый взгляд, а останется единой.

В дальнейшем, в этом курсе будут рассматриваться только двухсторонние поверхности.

Определение. Поверхность с выбранной стороной (совокупность нормалей) называется ориентированной поверхностью.

Явно заданную поверхность : z = f(x,y) называют положительно ориентированной, если cos (n,k) > 0. Поверхность : y = f(x,z) называют положительно ориентированной, если cos (n,j) > 0. Поверхность : x = f(y,z) называют положительно ориентированной, если cos (n,i) > 0.

Для замкнутой поверхности положительной ориентацией называется выбор внешней нормали

2. Определение поверхностного интеграла 2-го рода

Рассмотрим непрерывно дифференцируемую поверхность Ф: z = z(x,y) на D. Для заданного разбиения {Ф_k } этой поверхности и набора промежуточных точек {М_k } обозначим n_k единичную нормаль в точке М_k к поверхности Ф. Через D_k обозначим проекцию Ф_k на плоскость x y. Для функции f , определенной на Ф рассмотрим интегральные суммы вида

 = sign cos(k, n_k).

Здесь k орт оси Oz. Отметим, что в данном определении множитель sign cos(k, n_k) не зависит от k и может принимать два значения, в зависимости от ориентации поверхности, либо 1, либо –1.

Замечание. Таким образом, в случае задания поверхности в виде z = z(x,y) этот множитель не зависит от k и интегральные суммы будут равны  = , либо  = в зависимости от ориентации поверхности.

Поверхностным интегралом 2-го рода называется предел сумм  при стремлении к нулю характеристики разбиения, при условии, что этот предел не зависит от выбора разбиения и промежуточных точек. Обозначается интеграл

=.

Замечание. Если Ф^- та же поверхность с противоположной ориентацией, то

= .

Аналогично определяются интегралы dydz , dzdx , в случае, если поверхность однозначно проектируется на соответствующие координатные плоскости. В этих определения порядок дифференциалов менять нельзя. Интегральные суммы будут иметь вид sign cos(i, n_k), sign cos(j, n_k). i,j –орты координатных осей Ox, Oy.

Рассмотрим векторное поле V=(P,Q,R) определенное на ориентированной поверхности Ф, которая однозначно проектируется на все координатные плоскости. В этом случае можно рассмотреть интеграл

= ++ .

Если поверхность Ф разбивается на отдельные части Ф_k, каждая из которых однозначно проектируется на все координатные плоскости, то определяется, как сумма интегралов по отдельным частям

=.

3. Существование и вычисление поверхностного интеграла 2-го рода

Ориентированная поверхность задана явно Ф : z = z(x,y) на D , с непрерывно дифференцируемой функцией z(x,y). R(x,y,z) – непрерывна на Ф. Тогда поверхностный интеграл

существует и вычисляется по формуле

= or Ф .

Здесь и в дальнейшем or Ф = 1 для положительно ориентированной поверхности и or Ф = -1 в противном случае.

Доказательство. Для заданных разбиений {Ф_k } , {D_k }, промежуточных точек {М_k} ={(x_k,y_k,z(x_k,y_k)} единичных нормалей n_k в точках М_k к поверхности Ф обозначим cos _k = cos (n_k ,k) . Тогда для интегральных сумм получим

 = sign cos _k = or Ф .

Из последнего равенства и следует требуемое утверждение. Аналогичные формулы имеют место для поверхностей вида y=y(z, x), x=x(y, z).

= or Ф , = or Ф .

4. Связь с интегралом 1-го рода

Как отмечалось ранее _k==или

D_k= , - третий направляющий косинус единичной нормали к поверхносити Ф в точке P_k. Если M_k_k и cos _k третий направляющий косинус единичной нормали к поверхносити Ф в точке M_k , то sign cos _k = sign cos _k . Поэтому для функции R(x,y,z), заданной на поверхности, получим

 = sign cos _k = sign cos _k =

cos _k =cos _k +(cos _k - cos _k ) .

Первая сумма является интегральной для , вторая сумма стремится у нулю при неограниченном измельчении разбиения. Последнее утверждение следует из ограниченности функцииf (первая теорема Вейерштрасса) и равномерной непрерывности функции cos  (x,y,z) (функция – косинус угла между нормалью к поверхности и осью z является непрерывной функцией на поверхности. Предполагается, что D-компакт). Таким образом, мы получаем формулу, связывающую поверхностные интегралы 2-го и 1-го рода

= .(1)

Определение. Поверхность, которая однозначно проектируется на все координатные плоскости, будем называть поверхностью типа А . Поверхность называется допустимой, если она непрерывно дифференцируема, имеем везде ненулевую нормаль и допускает разбиение на конечное число поверхностей типа А.

Для допустимых поверхностей Ф, доказанная формула будет верна по отношению ко всем координатным плоскостям. В частности, если на поверхности определено непрерывно дифференцируемое поле V=(P,Q,R), то

P dydz +Q dzdx+R dxdy = (P cos  +Q cos  + R cos ) dS , (2)

где cos  , cos , cos  - направляющие косинусы нормали к поверхности. Эти формулы можно получить из (1) циклической перестановкой переменных. Например, для интеграла в формуле(1) необходимо заменить R на Q , y на x , z на y , x на z, cos  на cos  (См. рис. Заменяем 2 на 3).

5. Простейшие свойства поверхностного интеграла 2-го рода

Введем следующие обозначения dS=ndS=(cos , cos , cos ) dS. Это позволяет использовать векторное обозначение для интеграла 2-го рода

P dydz +Q dzdx+R dxdy = (V,dS).

Формула (2) в этих обозначениях выглядит следующим образом

(V,dS) = (V,n) dS (2)

Замечание.Как это следует из формул вычислния площади поверхности, dS=|N|dxdy для поверхности z(x,y) и dS=|N|dudv для параметрически заданной поверхности. Это можно использовать при вычислении поверхностных интегралов. Например, для параметрически заданной поверхности можно записать

(V,dS) = (V,n) dS=(V,n) |N|dudv=(V, N)dudv .

Отметим свойства интеграла 2-го рода

1) (V,dS) = -(V,dS)

2) (V + W, dS) = (V, dS) + (W, dS)

3) (V,dS) = (V,dS) + (V,dS)

4) |(V,dS)|  max |V|

Все эти свойства являются следствием соответствующих свойств интеграла 1-го рода и формулы (2).

Пример 1 (4352.2). Найти статические моменты однородной треугольной пластинки x+y+z=a, x0, y0, z0 относительно координатных плоскостей.

Требуется вычислить интегралы,,.

Плотность распределения массы =1. ===.

Пример 2 (4353). Найти момент инерции относительно оси Oz однородной сферической оболочки x²+y²+z²=a² , z0.

Требуется вычислить интеграл .

Плотность распределения массы  возьмем равной 1. Найдем длину вектора нормали для сферических координатx=a cos cos , y=a cos sin , x=a sin

=

a²(cos² cos, cos² sin, sin cos), =a² cos  .

Эта величина равна модулю якобиана, отображения определяемого сферическими координатами.

Тогда, используя сферические координаты для параметрического задания верхней полусферы, ( область изменения параметров - прямоугольник )

=======.

Отметим, что в этом примере речь не идет о замене переменных.

Пример 3 (4354). Найти координаты центра тяжести однородной поверхности , вырезанной поверхностью.

Координаты центра тяжести: ,,.

Считаем плотность распределения масс равной 1. Вес поверхности=====.

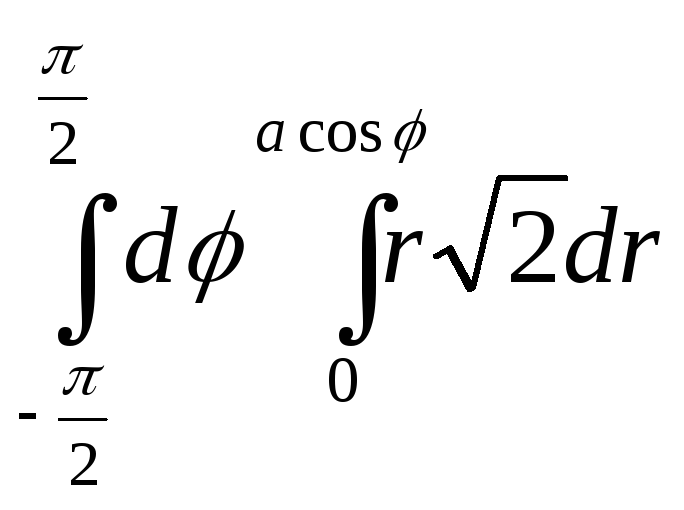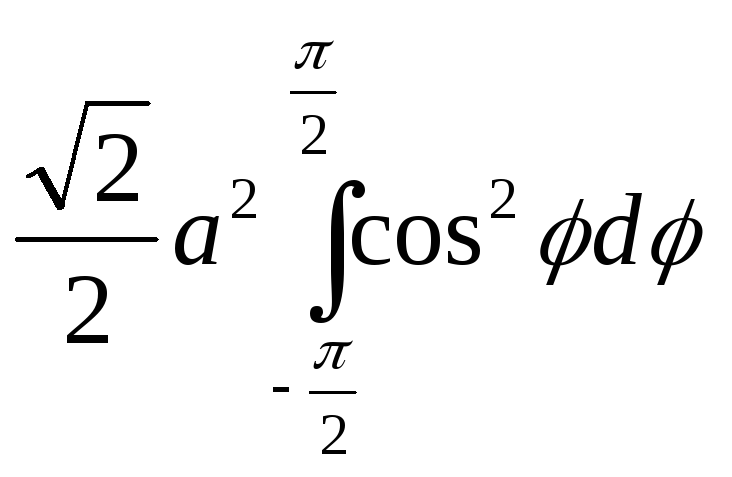=====.X = .Y = 0 из соображений симметрии.

===y==.Z=.

Пример 4 (4362).

Вычислить ,Ф-внешняя сторона сферы x²+y²+z²=a².

(V,dS) = (V,n) dS===aФ=.

Пример 5 (4365).

Вычислить ,Ф-внешняя сторона эллипсоида .

... Обозначим через - верхний полуэллипсоид, а через D его проекцию на плоскость xOy. Учитывая ранее сделанное замечание и симметрию относительно координатных осей, получим

=2=====.