РГР – 2 Вариант №4.
Задание №1
Время работы элемента до отказа подчинено экспоненциальному закону распределения с параметром λ. Требуется вычислить количественные характеристики надежности элемента p(t),q(t),f(t),mt.
вар |
λ 1/час |
t час |
4 |
1.5*10-6 |
1000 |
P(t) - вероятность безотказной работы изделия на интервале времени от 0 до t при экспоненциальном законе распределения вычисляется по формуле:
Q(t) - вероятность отказа изделия на интервале времени от 0 до t изделия при экспоненциальном законе распределения вычисляется по формуле:
F(t)-частота отказов изделия или плотность вероятности времени безотказной работы изделия при экспоненциальном законе распределения вычисляется по формуле:
mt - среднее время безотказной работы при экспоненциальном законе распределения вычисляется по формуле:
Таким образом, произведя соответствующие вычисления, получим следующие результаты:
Задание №1 |
|
|
Решение |
|
Дано: |
|
p(t)= |
0,998501124 |
|
λ= |
0,0000015 |
q(t)= |
0,001498876 |
|
t= |
1000 |
f(t)= |
1,49775E-06 |
|
Найти: |
|
mt= |
666666,6667 |
|
p(t),q(t), |
|
|
|
|
f(t),mt |
|
|
|
|
Задание №2
Время работы элемента до отказа подчинено нормальному закону с параметрами mt, σt, t. Требуется вычислить количественные характеристики надежности p(t), f(t), λ(t).
вар |
mt |
σt час |
t час |
4 |
10000 |
120 |
1200 |
P(t) - вероятность безотказной работы изделия на интервале времени от 0 до t при нормальном законе распределения вычисляется по формуле:
Q(t) - вероятность отказа изделия на интервале времени от 0 до t изделия при нормальном законе распределения вычисляется по формуле:
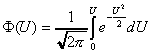
F(t)-частота отказов изделия или плотность вероятности времени безотказной работы изделия при нормальном законе распределения вычисляется по формуле:
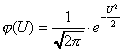
λ(t)- интенсивность отказов изделия при нормальном законе распределения вычисляется по формуле:
Таким образом, произведя соответствующие вычисления, получим следующие результаты:
Задание №2 |
|
|
Решение |
|
Дано: |
|
p(t)= |
0,500000 |
|
mt= |
10000 |
q(t)= |
0,5 |
|
t= |
1200 |
f(t)= |
0,008333333 |
|
σt = |
120 |
λ(t)= |
0,016666667 |
|
Найти: |
|
|
|
|
p(t), f(t), λ(t) |
|
|
|
|
Задание №3
Время работы изделия до отказа подчиняется закону распределения Релея. Требуется вычислить количественные характеристики надежности изделия p(t), f(t), λ(t), mt для t , σt.
вар |
σt час |
t час |
4 |
120 |
1000 |
P(t) - вероятность безотказной работы изделия на интервале времени от 0 до t при законе распределения Релея вычисляется по формуле:
Q(t) - вероятность отказа изделия на интервале времени от 0 до t изделия при законе распределения Релея вычисляется по формуле:
F(t)-частота отказов изделия или плотность вероятности времени безотказной работы изделия при законе распределения Релея вычисляется по формуле:
λ(t)- интенсивность отказов изделия при законе распределения Релея вычисляется по формуле:
mt - среднее время безотказной работы при законе распределения Релея вычисляется по формуле:
Таким образом, произведя соответствующие вычисления, получим следующие результаты:
Задание №3 |
|
|
Решение |
|
|
|
Дано: |
|
p(t)= |
0,000000000000000832396968 |
|||
σ = |
120 |
|
|
|
|
|
t = |
1000 |
f(t)= |
0,000000000000000057805345 |
|||
|
|
λ(t)= |
0,06944444 |
|
|
|
Найти: |
|
mt= |
150,36 |
|
|
|
p(t), f(t), λ(t), mt |
|
|
|
|
|
|