Решение задачи №3

План исследования функции на экстремум с помощью первой производной таков:

• находим область определения функции ;

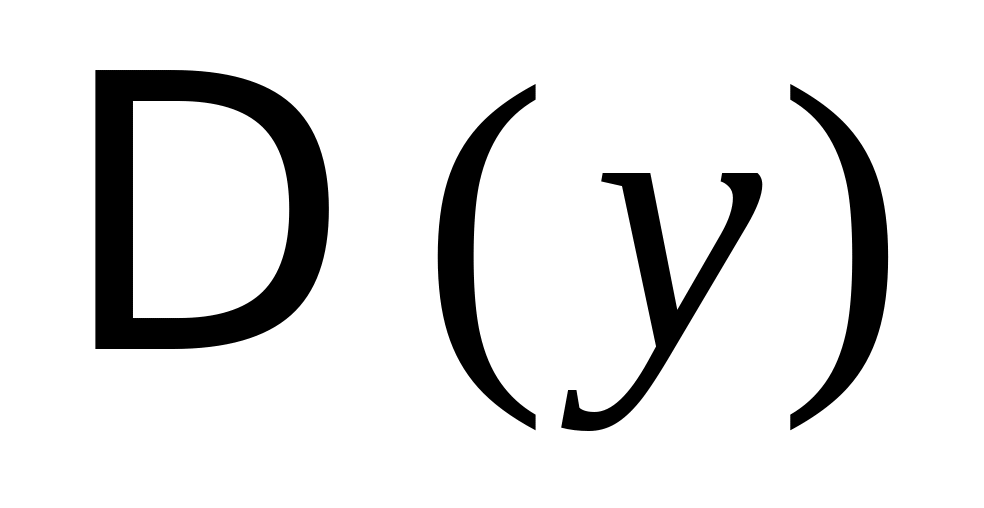• находим ;

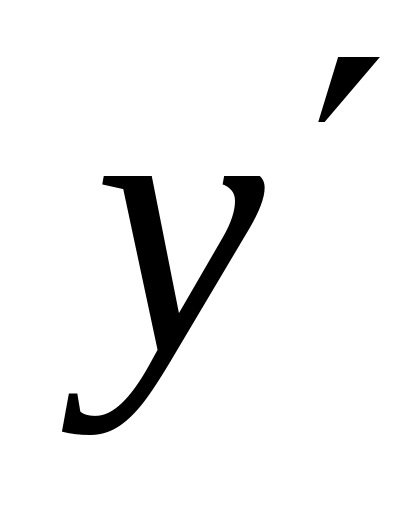• находим критические точки функции 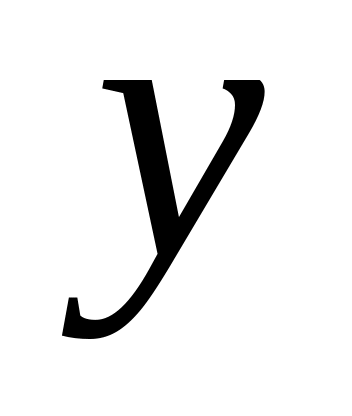(то есть те точки, в которых или не существует); пусть этими точками будут точки с абсциссами 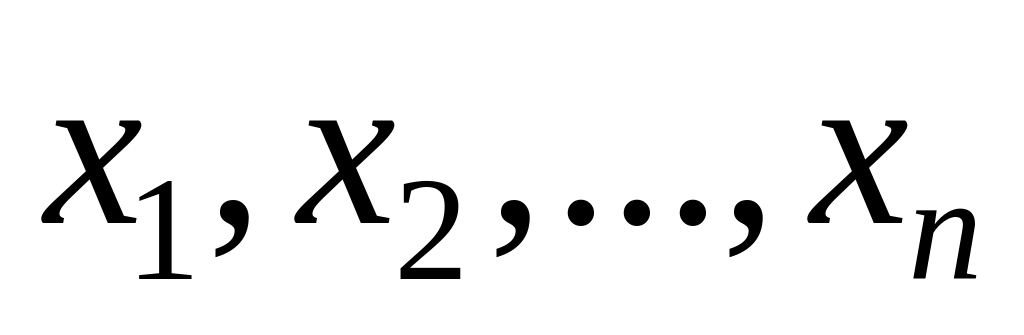, которые расположены в порядке их возрастания;

• разбиваем критическими точками на интервалы и внутри каждого интервала методом пробных точек находим знак ; все действия оформляем в виде таблицы (см. примеры 21–25 из лекции 8);

• используя теоремы 17 и 18 из лекции 8, определяем, на каких интервалах данная функция возрастает, на каких убывает, а также находим точки локального экстремума.

1. Рассмотрим функцию .

   • Очевидно, что .

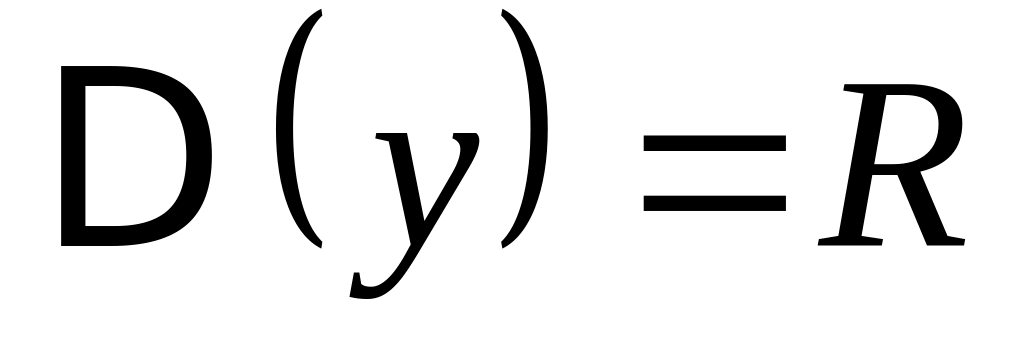   • Производная существует на всей числовой оси. Вычисляем: .

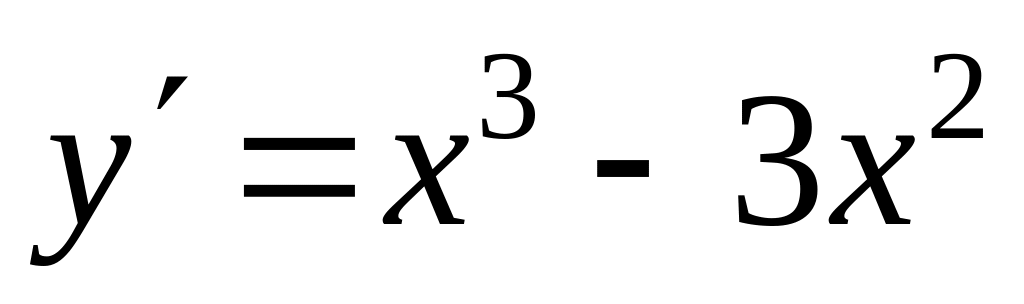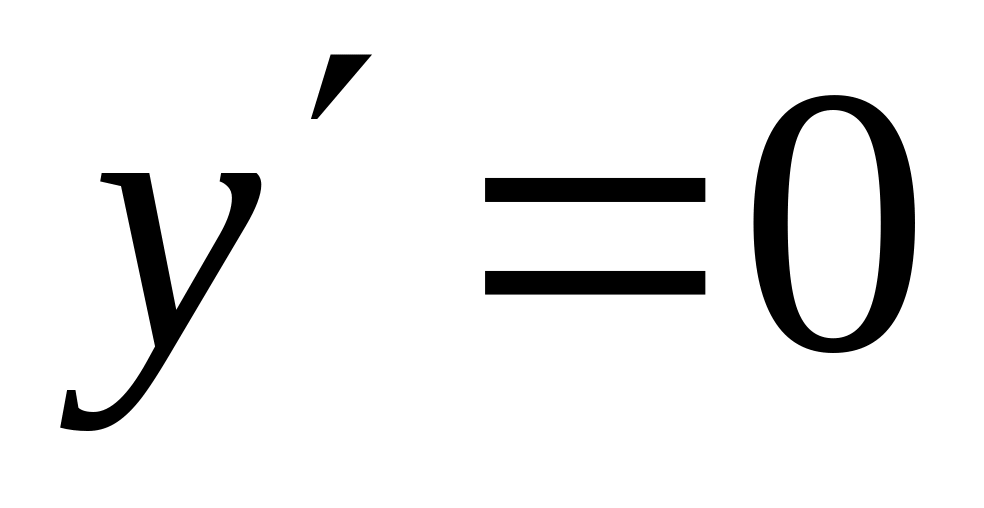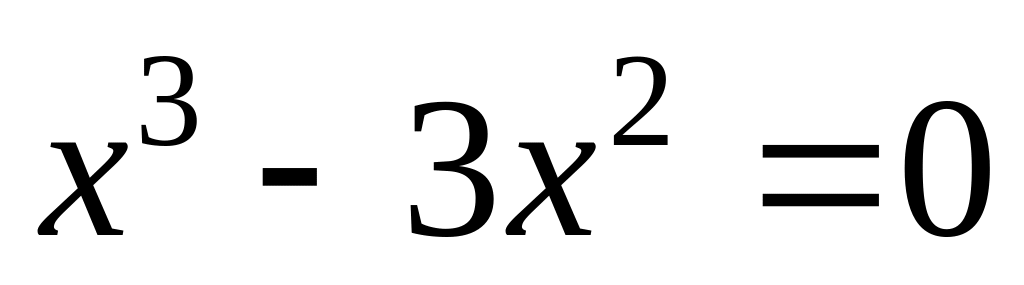
   • Решаем уравнение : 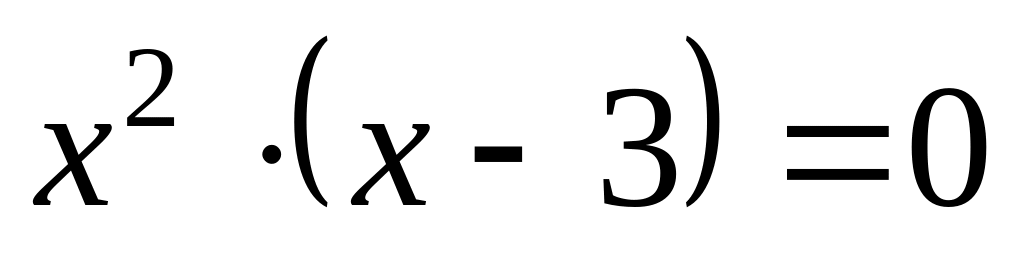, – критические точки.

   • Все дальнейшие действия оформляем в виде таблицы:

		0		3
	–	0	–	0	+
		0
		нет extr		min

Первая строка – это область определения функции, раздробленная на интервалы критическими точками. Выберем внутри каждого из этих интервалов произвольную точку и определим в этой точке знак первой производной . В интервале возьмем, например, точку и получаем ; в интервале возьмем точку и получаем ; в интервале возьмем точку и получаем (вместо этих точек в каждом из интервалов можно взять любые другие точки – результат будет тот же самый). Полученную информацию заносим во вторую строку таблицы.

• Применяя теорему 17, заключаем, что на интервалах и 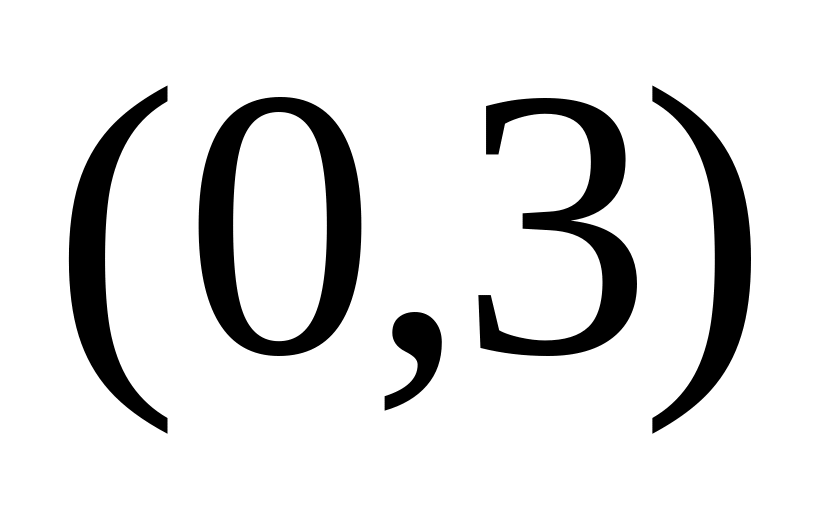функция строго монотонно убывает, а на интервале 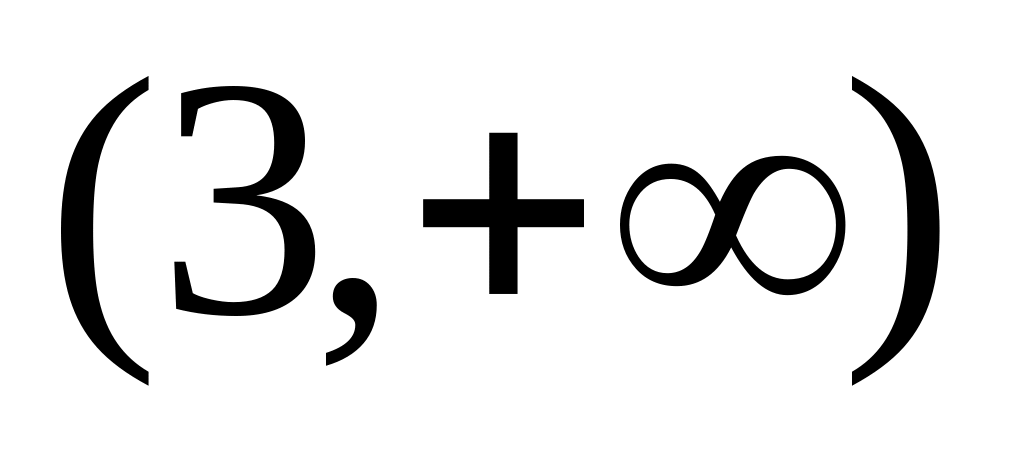– строго монотонно возрастает. Используя теорему 18, приходим к заключению, что в критической точке экстремума нет (как убывала функция до этой точки, так и убывает после нее); в критической точке имеем локальный минимум. Полученные результаты заносим в третью и четвертую строки таблицы.

2) Рассмотрим функцию .

• .

• .

• : , .

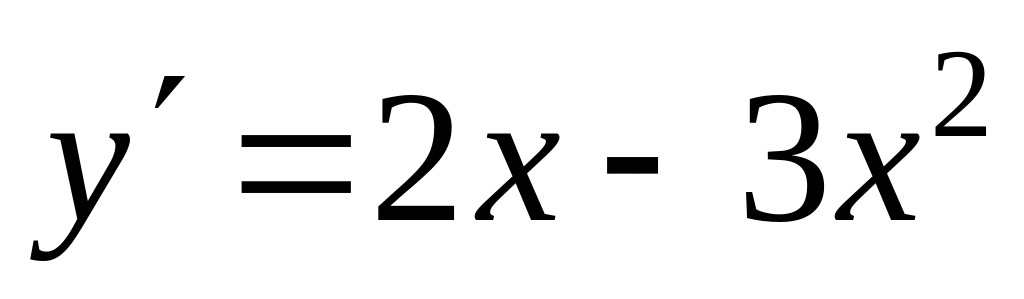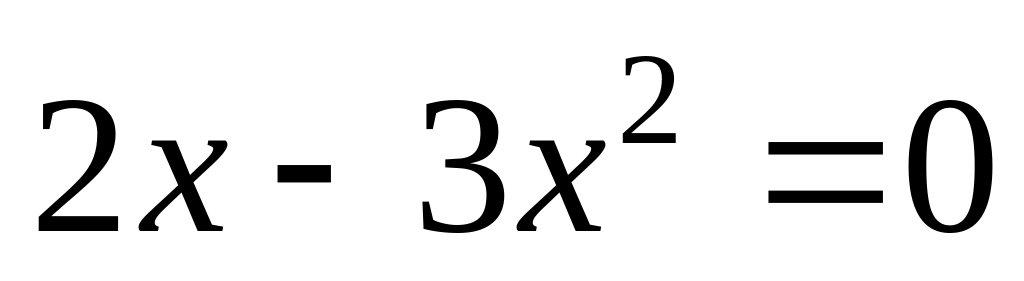
• Составляем таблицу:

		0
	–	0	+	0	–
		0
		min		max

Ясно, что – точка минимума, а ; – точка максимума, причем .

3) Рассмотрим функцию .

• .

• .

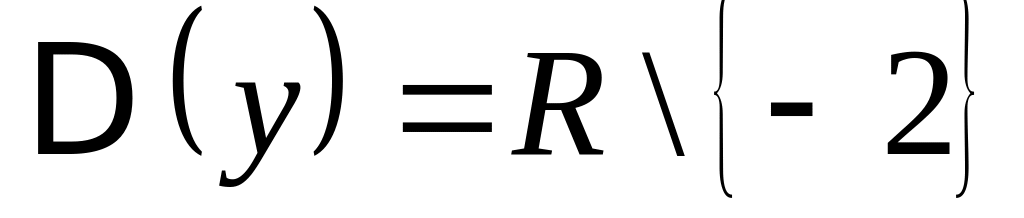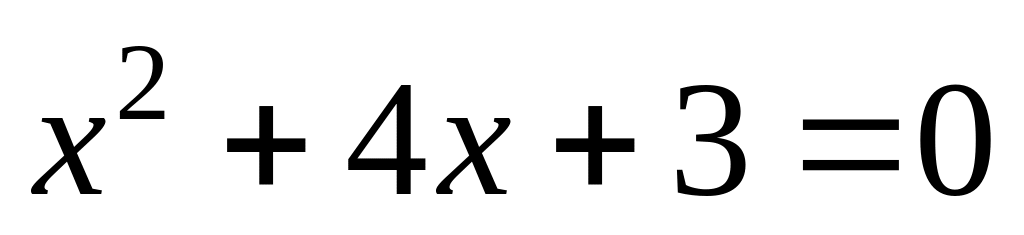
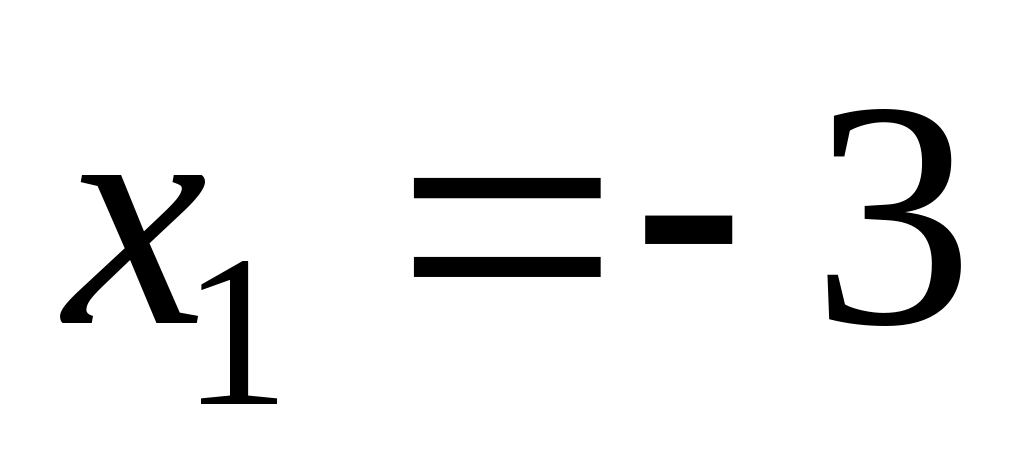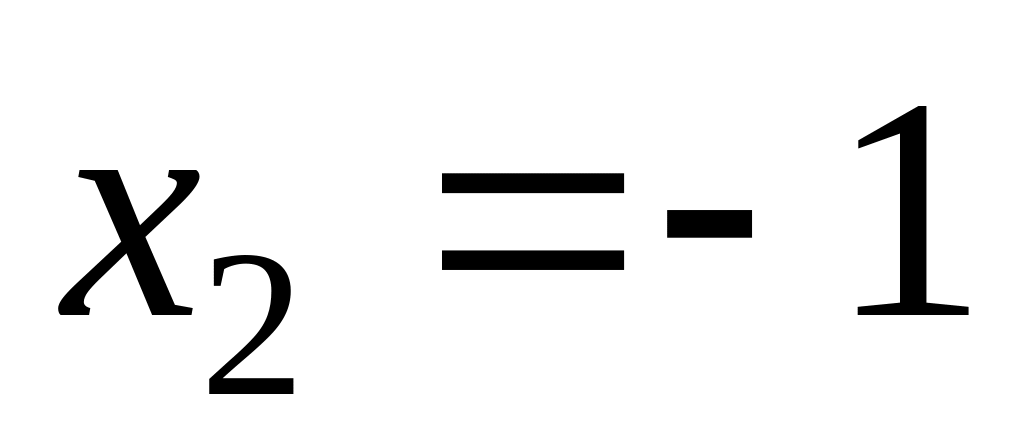• , – критические точки.

• Строим таблицу:

		–3
	–	0	+	+	0	–
		6			2
		min			max

Заметим, что мы не внесли в первую строку таблицы значение аргумента , так как оно не входит в . Итак, получаем: – точка минимума и , а – точка максимума, причем .

4) Рассмотрим функцию .

• .

• .

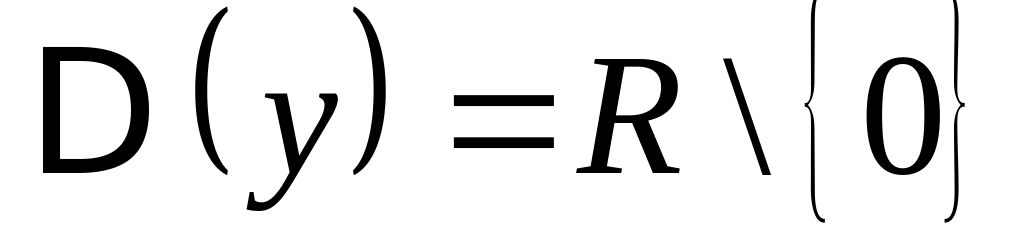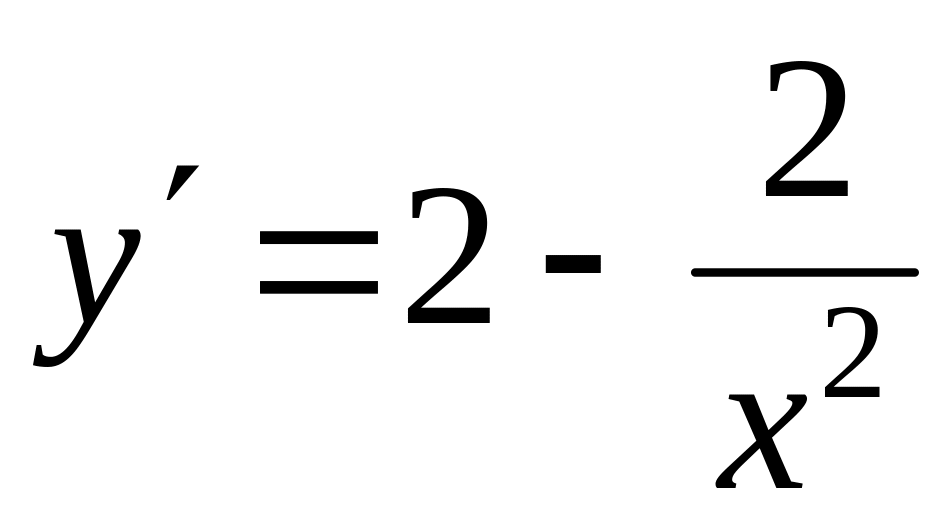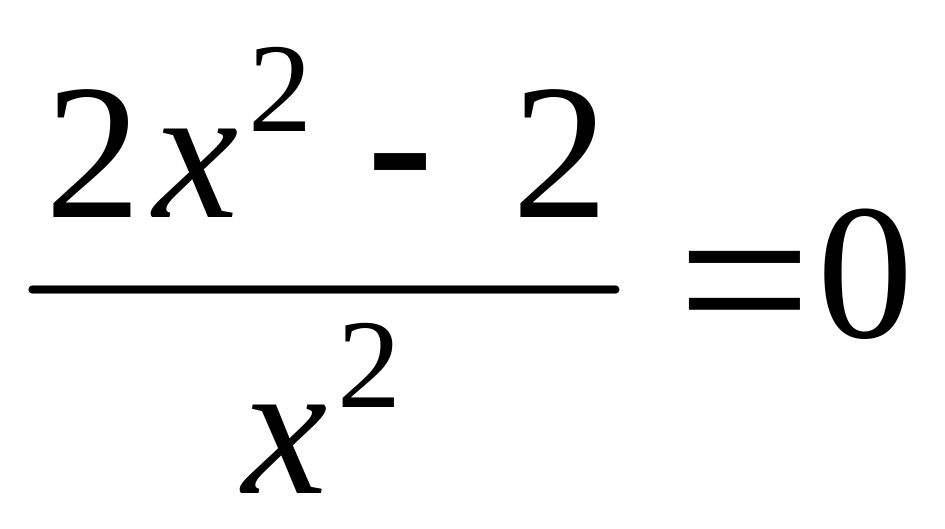
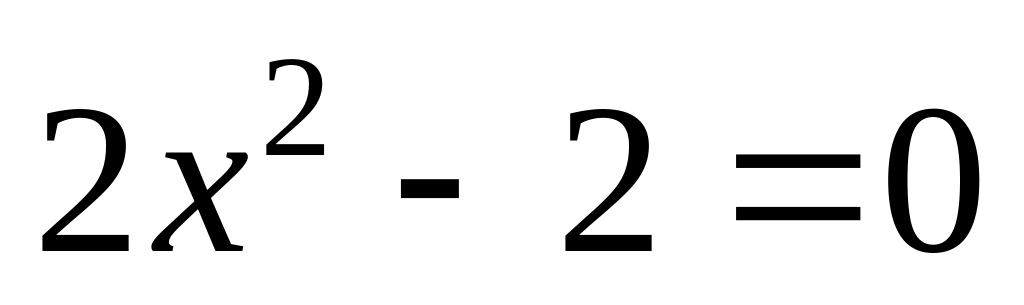
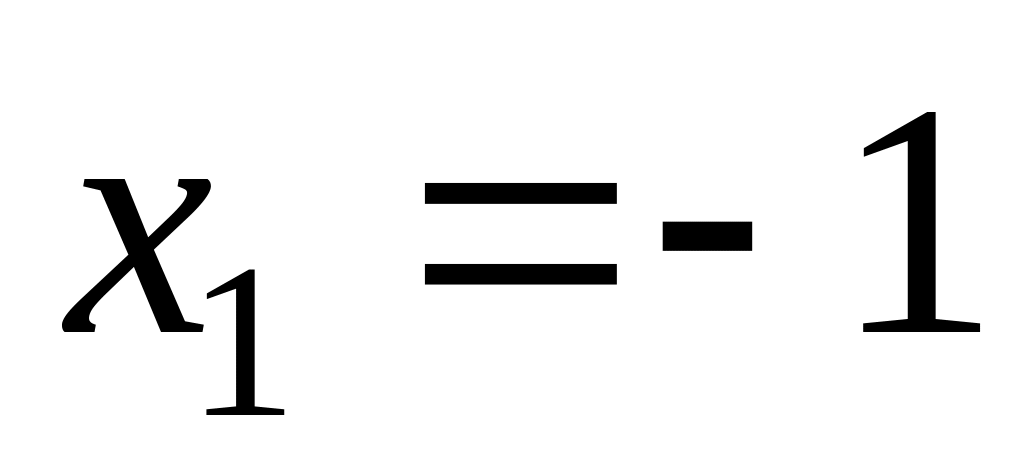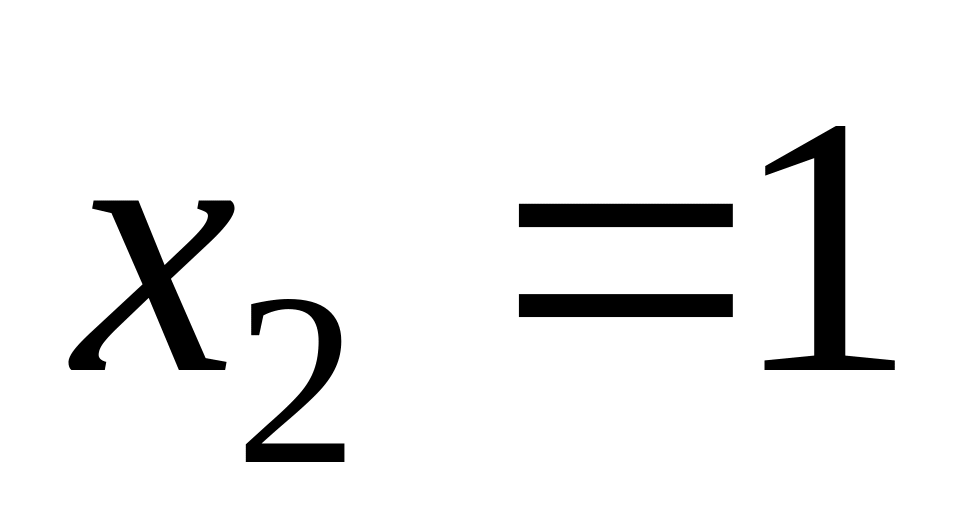• , – критические точки.

• Строим таблицу:

	+	0	–	–	0	+
		-4			4
		max			min

Итак, – точка максимума и , – точка минимума и .

5) Рассмотрим функцию .

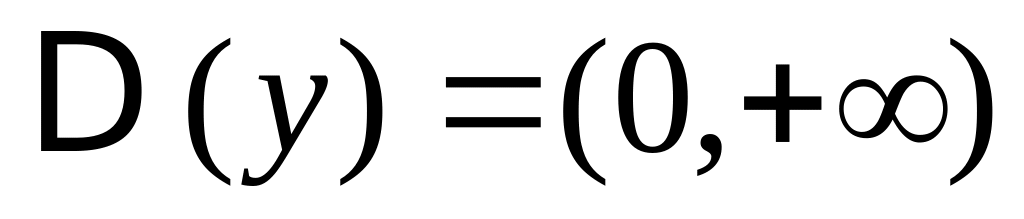• , так как логарифм существует только для положительных значений аргумента.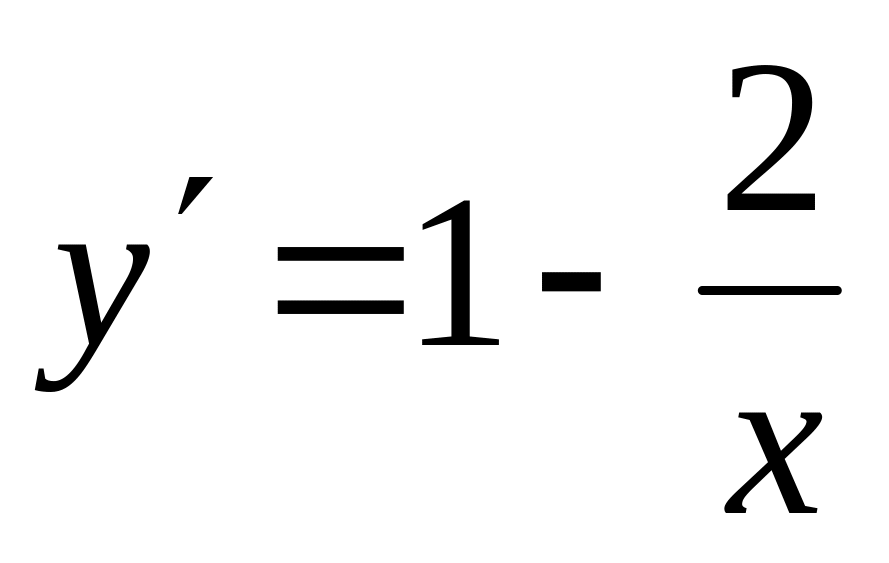

• .

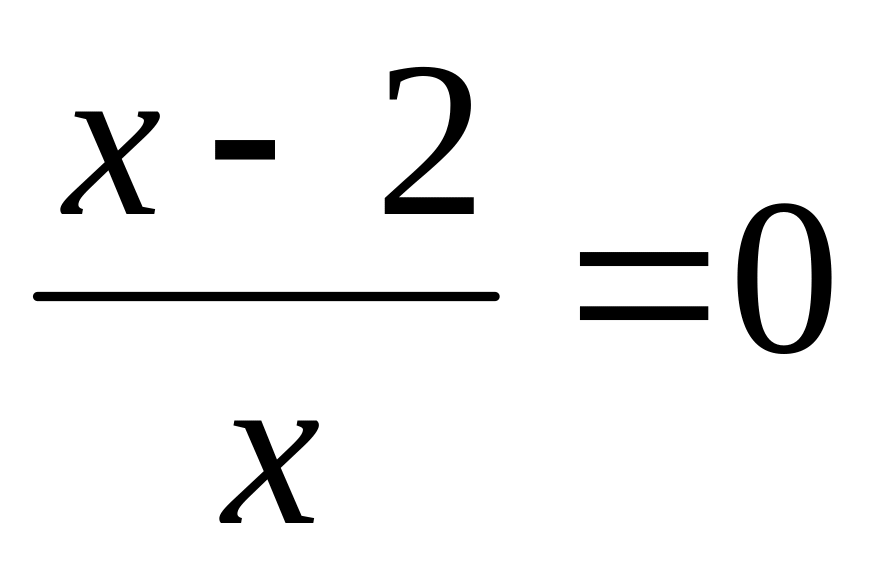
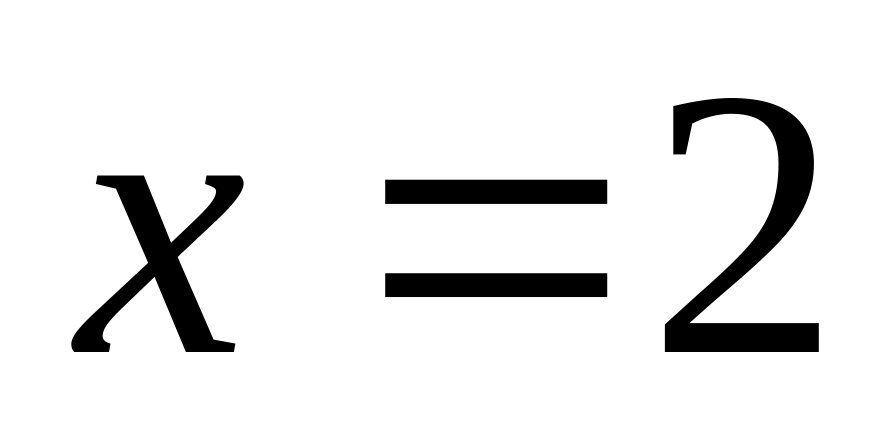• – критическая точка.

• Строим таблицу:

		2
	–	0	+
		min