Характеристические числа системной матрицы
Уравнение (4.25) характеризуется числами, удовлетворяющими этому уравнению. Они называются корнями уравнения, и могут, в общем случае, иметь действительные и мнимые составляющие, а их количество равно максимальной степени полинома левой части. Характер корней (действительные, мнимые, комплексные) и численные значения составляющих являются весьма информативной характеристикой собственных динамических свойств ДС с однородной частью ММ в виде (4.17). Поэтому для них введено особое понятие.
Корни характеристического уравнения (4.25) называются характеристическими или собственными числами (значениями), или спектром матрицы .
Характеристические значения системной матрицы обладают рядом важных для практики решения задач управления свойств.
а) Собственные значения либо действительны, либо образуют комплексно-сопряженные пары.
б) Если известны характеристические числа матрицы , то ее характеристический полином может быть представлен в виде
.
в)
Сумма характеристических чисел матрицы
равна ее следу и коэффициенту при
с обратным знаком:
.
г) Произведение характеристических значений матрицы равно определителю этой матрицы и алгебраически связано со свободным членом полинома (4.23) соотношением
.
д)
Если
- характеристическое значение матрицы
,
то оно же является характеристическим
значением транспонированной матрицы
.
е) Если - действительная симметрическая матрица, то все ее характеристические значения действительны.
ж)
Характеристические числа подобных
матриц
и
совпадают.
Замена базиса и эквивалентные преобразования МВ ММ. В 4.1 показано, что ММ исследуемой ДС в переменных состояния, реально существующих в объекте, получается на основе фундаментальных физических законов функционирования исследуемой динамической системы. Она является математическим эталоном, с которым должны сверяться любые варианты ММ.
Достаточно
общей математической формой такой
модели для линейных систем является
система матрично-векторных уравнений
(4.16). Эта система всегда записана
относительно некоторого базисного
вектора
.
Его компоненты должны быть разнородными
переменными, образующими независимые
координаты в пространстве состояний.
В рассмотренном в 4.1 примере этими
компонентами являются высота
и скорость движения
тела.
Линейное
пространство
,
образованное этими переменными как
координатами, является конечномерным
с размерностью
.
В нем существует
линейно-независимых векторов
,
а любой
-й
вектор линейно зависим от них. Согласно
положениям векторной алгебры любые
линейно-независимых векторов
заданных в определенном порядке в
-мерном
пространстве являются его базисом. Для
линейной независимости векторов
необходимо и достаточно, чтобы ранг
матрицы, составленной из них, был равен
.
Для
любой конкретной ДС форма (4.16) не является
единственной в смысле значений элементов
этих матриц. Конкретные значения
элементов зависят от структуры базиса
в пространстве состояний. Так, в
рассмотренном в (4.1) примере базис
пространства состояний образовывался
двумя векторами:
и
.
То, что это базис, подтверждается
невырожденностью матрицы, составленной
из этих векторов:
.
В пространстве состояний, образованном
координатами
и
можно построить и другие базисы, например,
и
.
Это также подтверждается невырожденностью
матрицы, составленной из новых векторов:
.
Таким образом, любое -мерное линейное пространство имеет бесконечное множество различных базисов. Так как же и зачем можно переходить от одного базиса к другому? На первый вопрос ответить достаточно просто.
Пусть
наряду с имеющимся базисом
,
в котором получена МВ ММ, существует
другой базис
,
в котором может быть описана моделируемая
система. Значит должна существовать ММ
такой же, как и (4.16) структуры
|
(4.16*) |
которая описывает поведение исследуемой ДС в новом базисе.
Поскольку эти две формы одной и той же ММ должны быть эквивалентны, переменная в одном базисе должна быть связана с переменной в другом ба базисе через некоторое преобразование. Из линейной алгебры известно, что любое преобразование вектора в линейном пространстве задается выражением
|
(4.26) |
,где должна быть квадратной и невырожденной матрицей.
Подстановка (4.26) в (4.16) дает, после преобразования, уравнение
|
(4.27) |
сопоставление (4.16*) и (4.27) к следующим формулам преобразования матриц ЛДУ при замене базиса:
|
(4.28) |
Таким образом, любое невырожденное преобразование в виде квадратной матрицы размерностью может быть использовано для получения ММ ДС в некотором новом базисе. То есть, любая ДС может быть описана в бесконечном количестве различных базисов.
Для иллюстрации применения полученного результата ниже рассматривается пример преобразования системы (4.16), заданной матрицами
|
|
.Для преобразования базиса взята матрица
|
|
.
Применение
формул (4.28) требует нахождения обратной
матрицы
:
|
|
В результате матричные вычисления дают новую системную матрицу
=
=
,
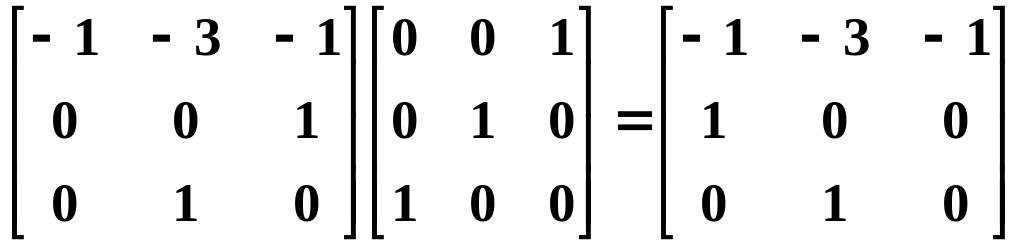матрицу входов и наблюдения по состоянию в новом базисе
,
.
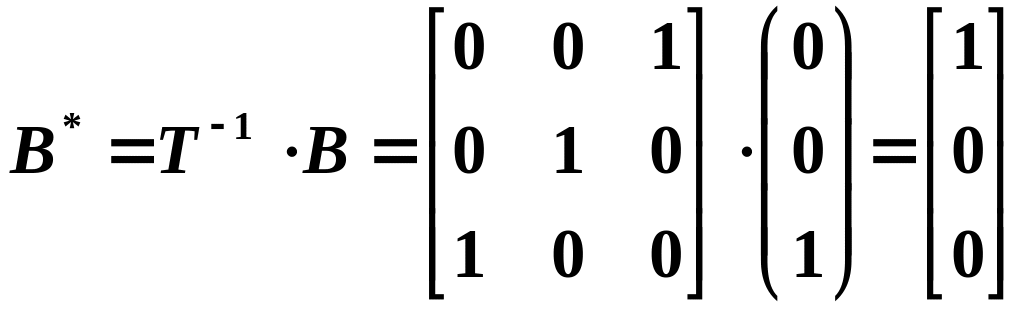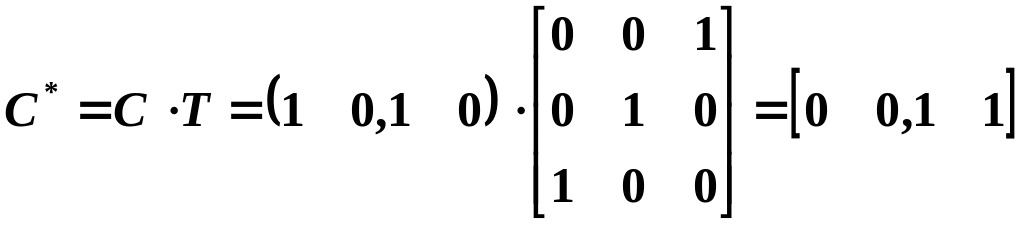Из-за отсутствия места, вынуждены отослать читателя к работам по теории систем и дифференциальных уравнений [38, 39, 36, 54 и пр.]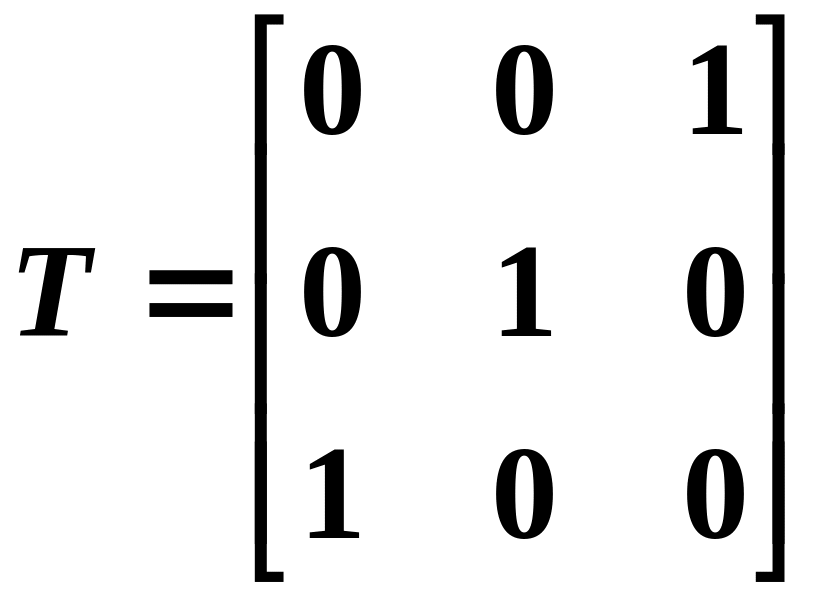