Матрично-векторные формы представления математических моделей. Получение, преобразование, исследование

1. Математические модели динамических систем в пространстве состояний

   1. 

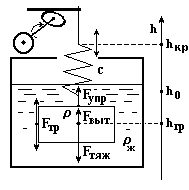
      Рис. 1 Механическая система и переменные состояния

      Математическая модель (ММ) динамической системы, полная по внутренним переменным. Есть груз массой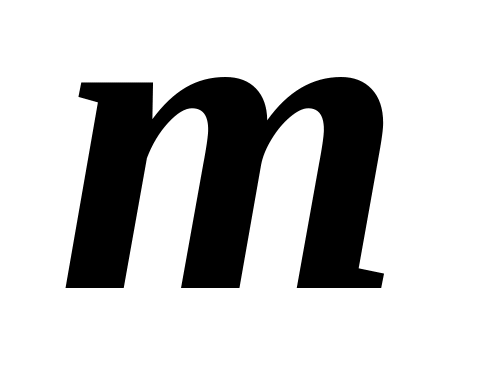 , пружина с жесткостью , жидкостное трение с коэфф. . Объект на рис. 1 с обозначениями: - силы тяжести, упругости пружины, выталкивания и трения жидкости соответственно; - плотности груза и жидкости; - положение крепления пружины и центра тяжести груза, переменная независимое входное воздействие.

(1) , где - действующие на груз силы определяемые следующими выражениями:

. Подставляя их в (1) и преобразуя, можно получить уравнение

(2) , где и - номинальные координаты.

Уравнение (2) является «вход-выходной» формой записи дифференциального уравнения (ДУ).

Такая форма ММ не однозначно оценивает состояние системы в произвольный момент времени и закон ее движения для при известных и . Например, для различных начальных значений в (2) и для одних и тех же и решения уравнения будут разными. Уравнения однозначно решаются при дополнительном задании начальных условий по производной .

Таким образом, для полного описания состояния исследуемой системы необходимо привлечь к рассмотрению вторую переменную - скорость . Тогда уравнение (2) можно записать в форме Коши

(3)

Для унификации математических исследований в теории динамических систем принято обозначать переменные, характеризующие движение объекта через х. Управляющее воздействие принято обозначать . Тогда, по обозначению, можно принять , ,

.

Тогда ММ (3) можно записать в единой матрично-векторной форме:

(4) ,

Поскольку и - переменные, описывающие состояние исследуемого объекта, вектор , образованный этими переменными, называют вектором состояния (ВС) динамической системы (ДС). Координаты ВС в пространстве этих переменных, называемом пространством состояния (ПС), однозначно определяют собственное состояние ДС, дальнейшее ее самостоятельное (собственное) движение, а также, при известном входном воздействии , вынужденное движение.

Сама система ДУ первого порядка (3) или (4) есть ММ в ПС для рассматриваемого объекта.

2. Математические модели ДС и представление переменных в приращениях. (Полученная выше ММ механической системы - классический пример изначально линейной ММ. Ее матрично-векторная форма представлена уравнением (4). Она получена и представлена в абсолютных физических единицах относительно выбранной при моделировании, в общем-то, совершенно произвольной точки в принятой системе координат, что привело к появлению в выражении дополнительной константы . Естественно, такая неопределенность при моделировании не слишком полезна, приводит к внешне неодинаковой форме результатов у разных исследователей и, в некоторых случаях, приводит к неудобствам при оценке количественных результатов.

Другим поводом для обсуждения данного вопроса является часто используемое в теории управления преобразование Лапласа, позволяющее перевести в алгебраическую область многие математические операции над линейными ДУ. Это преобразование эффективно и позволяет пользоваться удобным аппаратом передаточных функций только при нулевых начальных значениях тех переменных, которые находятся под знаками дифференцирования.)

Эти проблемы стимулировали в ТАУ переход к приращениям - приему преобразования ММ. Он состоит в формульной замене переменных на сумму их номиналов и варьируемы добавок, называемых приращениями. Таким образом, замена произвольной переменной в преобразуемом уравнении производится по формуле (5) , где - некоторое номинальное для исследуемого режима функционирования ДС значение переменной; - ее переменная составляющая.

В качестве выбирают характерное для ДС установившееся значение переменной. В примере номиналом входного воздействия удобно взять средний для ДС уровень крепления пружины . Тогда номинал положения груза получится из уравнения статики ДС. Его можно получить из ДУ (3), из равенства нулю всех производных - (6) . Подставив (5) в (3) и обозначив , , а также, имея в виду, что и , можно записать уравнения системы (3) в приращениях

(7)

Переобозначение , , , дает матрично-векторное уравнение (МВУ) (8) , линейной ДС, структура и математические свойства которого определяют свойства самой ДС.

3. Характеристика переменных пространства состояний. В ТАУ все переменные, как характеризующие состояние системы, так и влияющие на ее движение, разделяются на три группы.

Первая группа - входные переменные (входы, входные воздействия). Они делятся на две подгруппы по их отношению к цели управления.

Часть воздействий являются управляющими: или для автоматизируемого объекта - , или для САУ - .

Другие воздействия являются возмущающими для данной системы (помехой) - . Эти переменные представляют собой сигналы, извне влияющие на поведение исследуемой динамической системы (объекта или САУ).

Ко второй группе переменных относятся выходные переменные (выходы). Они обычно обозначаются и характеризуют наблюдаемую при работе реакцию системы на входные воздействия. Выходные переменные всегда представлены реальными физическими величинами, отражающими ход технологического процесса управляемой технической системы и, по определению, являются выходами и ОУ и САУ одновременно. Но они позволяют оценить лишь некоторые свойства и аспекты поведения системы, представляющие интерес для технолога процесса, но не отражают полностью ни текущее состояние ОУ, ни динамику его изменения.

Третью группу образуют переменные состояния (координаты в пространстве состояний). Эти переменные принято обозначать . Они образуются совокупностью некоторого количества переменных, необходимого и достаточного для того, чтобы полностью описать поведение во времени исследуемой системы относительно текущего состояния при известных входных воздействиях.

(В рассмотренном примере процедура построения ММ приводит к выделению переменных трех указанных групп. Естественной выходной переменной является координата центра тяжести груза . Она же - одна из переменных состояния. В состав ПС пришлось включить вторую - , поскольку только 2 ПС могут однозначно описать состояние ОУ 2 порядка. Входные воздействия представлены , которая в зависимости от технологии ОУ м.б. как управлением, так и возмущением. Их могло быть больше: в условия примера можно ввести перемещение емкости, изменение уровня и плотности последней и т.п.)

Рис. 2. Условная схема формирования ПС и выходов ДС

В общем случае ДС может быть схематически изображена в виде т.н. «черного ящика» с некоторым числом и входных и выходных каналов, как это показано на рис. 2. Входные каналы на этом рисунке представляют собой совокупность входных переменных или входных воздействий , выходные каналы - совокупность выходных переменных или выходных координат системы. Промежуточные переменные или координаты состояния , в общем случае, могут быть отнесены к содержимому «черного ящика» и, таким образом, скрыты от наблюдателя. В рассмотренном выше примере это относится к переменной , не наблюдаемой в качестве выходной. Величины , и для ДС являются функциями времени, т.е. , и .

Для удобства совокупности входных, выходных и вспомогательных переменных представляются в виде векторов входа, выхода и состояния динамической системы

(9) ; ; .

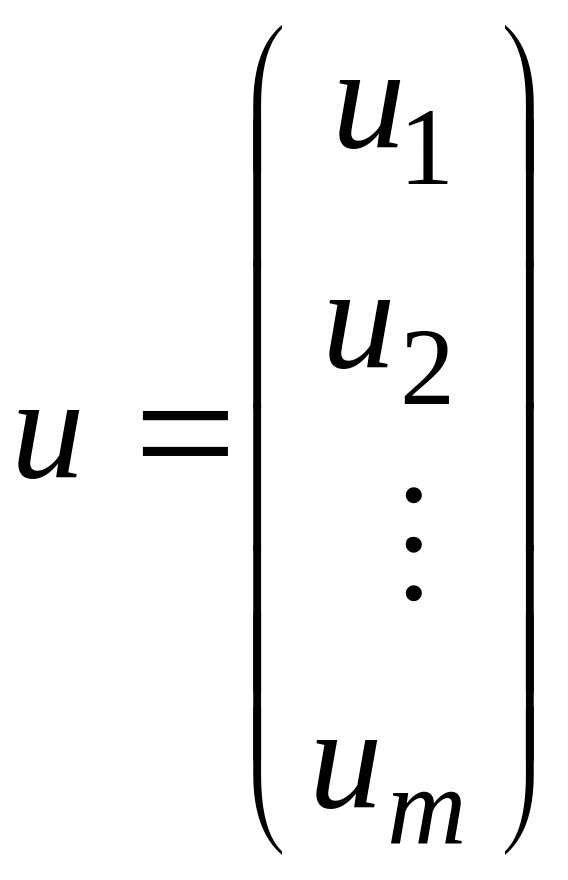(В примере переменные и являются скалярами, но это лишь частные случаи векторов для ).

Рис. 3 Пространство состояний колебаний груза

Множество составляющих вектора входа образует пространство входов, а множество составляяющихвектора выхода образует пространство выходов ДС. В примере эти пространства одномерны, т.е. м.б. представлены числовой осью. Аналогично, множество составляющих вектора состояния , образует пространство состояний системы. В примере оно м.б. представлено плоскостью с координатами и ( и ).

(Обычным результатом аналитического построения ММ являются ДУ. Они - наиболее универсальный инструмент описания динамики, т.к. ориентированы на неявный способ задания решений. ДУ можно получать в виде уравнений высокого порядка, составленных относительно выходных переменных, и названных «вход-выходной» формой представления, так и в форме Коши. Далее рассматриваются ДУ, представленные именно этой формой).

4. Формы представления ММ линейных ДС. Уравнение состояния. Анализ структуры (8) показывает, что такая форма ММ задает явно связь интенсивности изменения ПС с их текущими значениями и входными воздействиями. При этом ПС задаются неявно - как решения ДУ состояния для конкретных условий движения ДС.

В ТАУ ОУ и САУ подвержены воздействиям двух групп: управляющим и возмущающим. Поэтому

(10)

В (8 и 10) называется системной матрицей: ее структура и значения элементов определяют фундаментальные свойства описываемой уравнением ДС.

Во-первых, - квадратная матрица, - порядок ДУ - порядок ДС.

Во-вторых, она, как бы распределяет влияние координат состояния на закон движения системы, поскольку ее нулевые элементы исключают некоторые переменные состояния из соответствующих уравнений.

В-третьих, от знаков и значений элементов зависят фундаментальные свойства ДС, как устойчивость, управляемость, наблюдаемость и др.

Матрица в (8) называется матрицей входов. Ее роль в ДУ – распределение входных воздействий между строками системы. В уравнении формы (10) уже называется матрицей управляющих входов или матрицей управления. Тогда является в (10) матрицей возмущающих входов или матрицей возмущения.

(Использование записи (10) особенно удобно для ОУ. При замыкании его ММ уравнением УУ переменная из (10) исключается, а член остается, задавая структуру и характеристики воздействия возмущений на систему управления через ОУ. Использование в таких задачах уравнения (8) менее наглядно и все равно приводит к необходимости декомпозиции входов.Ъ

5. Формы представления ММ линейных ДС. Уравнение наблюдения. Однако уравнение состояния как ММ является неполной характеристикой ДС, так как переменные чаще всего бывают «скрытыми», т.е. ненаблюдаемыми, а, в ряде случаев, и вовсе абстрактными, т.е. не имеющими реального физического содержания. Но САУ нужна для целевой направленности работы реального объекта. Его технологическое состояние характеризуется реальными физическими переменными - выходными. Поэтому ее ММ должна быть дополнена выражениями, связывающими ее состояние с выходными переменными.

ПС, как и пространство решений ДУ состояния -мерно, совокупность ПС и входов полностью определяет состояние ДС. (Любая другая переменная системы однозначно задается этой совокупностью). Поэтому вектор выходных переменных в любой момент времени является функцией и . Таким образом, уравнение состояния в полной ММ ДС должно быть дополнено алгебраическим уравнением следующего общего вида:

(11) , которое принято называть уравнением наблюдения.

(Для рассмотренного примера это уравнение имеет вид простого равенства (в приращениях) - ).

Общая форма записи уравнений состояния – векторная. ДС может иметь не только несколько ПС, но и несколько выходов. Полученное для примера уравнение наблюдения должно быть записано в следующем виде: (12) , , где будет называться матрицей наблюдения по состоянию.

(Запись (12) уравнения состояния не является формальностью. Пусть в качестве выходной переменной в исследуемой механической системе рассматривается не положение груза, а сила жидкостного трения, испытываемой грузом (исследование эффектов вибраций). Тогда и матрица наблюдения по состоянию определится выражением ).

Форма (12) не универсальна. Если выходом является растяжка пружины, т.е. , то матрица наблюдения по состоянию задастся выражением , но второй компонент наблюдения в матричном уравнении отражен не будет. Значит, нужна другая форма матричного уравнения наблюдения: (13)

Такая форма дает возможность записать новое уравнение наблюдения, дополнив матрицу матрицей , назвав ее матрицей наблюдения по управлению. В практике ТАУ бывают случаи, когда на наблюдение влияют возмущения. Тогда матричное уравнение наблюдения должно иметь наиболее полный по форме вид (14) , где естественно назвать матрицей наблюдения по возмущению.

6. Формы представления ММ линейных ДС. Полное уравнение ДС. Таким образом, полной ММ ДС в пространстве состояний является пара векторных уравнений состояния (10) и наблюдения (14)

(15)

Таким образом, метод пространства состояний базируется на возможности и достаточности описания поведения многих ДС некоторым количеством дифференциальных уравнений первого порядка в полных производных. Переменные, производные которых формируют левые части этих уравнений, называются в теории управления переменными состояния. Уравнения (15) называются матрично-векторными (МВ) ДУ.

Этот подход лежит в основе т.н. современной теории управления.