18. Закон Био-Савара-Лапласа

Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 1) индукцию поля dB, равен

где dl - вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r - радиус-вектор, который проведен из элемента dl проводника в точку А поля, r - модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с направлением касательной к линии магнитной индукции. Это направление может быть найдено по правилу правого винта: направление вращения головки винта дает направление dB, если поступательное движение винта совпадает с направлением тока в элементе.

Модуль вектора dB задается выражением

где α — угол между векторами dl и r.

19. Применение Закона Био-Савара-Лапласа

Применение

Допустим требуется найти модуль магнитной индукции в центре очень тонкой (все витки уложены вблизи одной окружности) катушки с числом витков N, по которой течет ток .I Найдём магнитную индукцию, создаваемую одним витком катушки. Из формулы

получим модуль магнитной индукции как

где r - как следствие, радиус катушки - константа, (альфа) - угол между вектором r и dr (элемента витка), ввиду взаимной перпендикулярности, всегда равен 90 градусов. Проинтегрировав обе части получаем

где - сумма длин всех элементов проводника витка или длина окружности, тогда

Так как в катушке содержится N витков, то суммарный модуль магнитной индукции равен

20. Движение зарядов в магнитном поле. Сила Лоренца

Сила Лоренца

- сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.

где q - заряд частицы;

V - скорость заряда;

B - индукции магнитного поля;

a - угол между вектором скорости заряда и вектором магнитной индукции.

Направление силы Лоренца определяется по правилу левой руки:

Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца

Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию).

Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fл = 0 , и заряд в магнитном поле движется равномерно и прямолинейно.

Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной

и создает центростремительное ускорение равное

В этом случае частица движется по окружности.

Согласно второму закону Ньютона: сила Лоренца равнв произведению массы частицы на центростремительное ускорение

тогда радиус окружности

а период обращения заряда в магнитном поле

Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.

21. Основные особенности движения в этом случае можно выяснить, не прибегал к полному решению уравнений движения. Прежде всего, отметим, что действующая на частицу сила Лоренца всегда перпендикулярна к скорости движения частицы. Это значит, что работа силы Лоренца всегда равна нулю; следовательно, абсолютное значение скорости движения частицы, а значит, и энергия частицы остаются постоянными при движении. Так как скорость частицы u не изменяется, то величина силы Лоренца

остается постоянной. Эта сила, будучи перпендикулярной, к направлению движения, является центростремительной силой. Но движение под действием постоянной по величине центростремительной силы есть движение по окружности. Радиус r этой окружности определяется условием

откуда

Если энергия электрона выражена в эВ и равна U, то

(3.6) и поэтому

Кругообразное движение заряженных частиц в магнитном поле обладает важной особенностью: время полного обращения частицы по окружности (период движения) не зависит от энергии частицы. Действительно, период обращения равен

Подставляя сюда вместо r его выражение по формуле (3.6), имеем:

(3.7) Частота же оказывается равной

Для данного типа частиц и период, и частота зависят только от индукции магнитного поля. Выше мы предполагали, что направление начальной скорости перпендикулярно к направлению магнитного поля. Нетрудно сообразить, какой характер будет иметь движение, если начальная скорость частицы составляет некоторый угол с направлением поля. В этом случае удобно разложить скорость на две составляющие, одна из которых параллельна полю, а другая перпендикулярна к полю. На частицу действует сила Лоренца, и частица движется по окружности, лежащей в плоскости, перпендикулярной к полю. Составляющая Ut, не вызывает появления добавочной силы, так как сила Лоренца при движении параллельно полю равна нулю. Поэтому в направлении поля частица движется по инерции равномерно, со скоростью

В результате сложения обоих движений частица будет двигаться по цилиндрической спирали.

Шаг винта этой спирали равен

подставляя вместо T его выражение (3.7), имеем:

22. Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, которая равна (1) где Bn=Вcosα - проекция вектора В на направление нормали к площадке dS (α — угол между векторами n и В), dS=dSn — вектор, у которого модуль равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cosα (задается выбором положительного направления нормали n). Поток вектора В обычно связывают с контуром, по которому течет ток. В этом случае положительное направление нормали к контуру нами задавалось: оно связывается с током правилом правого винта. Значит, магнитный поток, который создается контуром, через поверхность, ограниченную им самим, всегда положителен.

Поток вектора магнитной индукции ФB через произвольную заданную поверхность S равен (2) Для однородного поля и плоской поверхности, которая расположена перпендикулярно вектору В, Bn=B=const и

Из этой формулы задается единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, который проходит сквозь плоскую поверхность площадью 1 м2, который расположен перпендикулярно однородному магнитному полю и индукция которого равна 1 Тл (1 Вб=1 Тл•м2). Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:

(3) Эта теорема является отражением факта, что магнитные заряды отсутствуют, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми. Следовательно, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные формулы. В качестве примера найдем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью μ, равна Магнитный поток сквозь один виток соленоида площадью S равен а полный магнитный поток, который сцеплен со всеми витками соленоида и называемый потокосцеплением, 23. На проводник с током в магнитном поле действуют силы, определяемые законом Ампера. Если проводник не закреплен (например, одна из сторон контура изготовлена в виде подвижной перемычки, рис. 177), то под действием силы Ампера он будет в магнитном поле перемещаться. Следовательно, магнитное поле совершает работу по перемещению проводника с током. Для определения этой работы рассмотрим проводник длиной l с током I (он может свободно перемещаться), помещенный в однородное внешнее магнитное поле, перпендикулярное плоскости контура. Сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера (см. (111.2)), равна Под действием этой силы проводник переместится параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, совершаемая магнитным полем, равна так как ldx=dS — площадь, пересекаемая проводником при его перемещении в магнитном поле, BdS=dФ — поток вектора магнитной индукции, пронизывающий эту площадь. Таким образом, (121.1) т. е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником. Полученная формула справедлива и для произвольного направления вектора В. Вычислим работу по перемещению замкнутого контура с постоянным током I в магнитном поле. Предположим, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения займет положение М', изображенное на рис. 178 штриховой линией. Направление тока в контуре (по часовой стрелке) и магнитного поля (перпендикулярно плоскости чертежа — за чертеж) указано на рисунке. Контур М мысленно разобьем на два соединенных своими концами проводника: AВС и CDА. Работа dA, совершаемая силами Ампера при рассматриваемом перемещении контура в магнитном поле, равна алгебраической сумме работ по перемещению проводников AВС (dA1) и CDA (dA2), т. е. (121.2) Силы, приложенные к участку CDA контура, образуют с направлением перемещения острые углы, поэтому совершаемая ими работа dA2>0. .Согласно (121.1), эта работа равна произведению силы тока I в контуре на пересеченный проводником CDA магнитный поток. Проводник CDA пересекает при своем движении поток dФ0 сквозь поверхность, выполненную в цвете, и поток dФ2, пронизывающий контур в его конечном положении. Следовательно, (121.3) Силы, действующие на участок AВС контура, образуют с направлением перемещения тупые углы, поэтому совершаемая ими работа dA1<0. Проводник AВС пересекает при своем движении поток dФ0 сквозь поверхность, выполненную в цвете, и поток dФ1, пронизывающий контур в начальном положении. Следовательно, (121.4). Подставляя (121.3) и (121.4) в (121.2), получим выражение для элементарной работы: где dФ2—dФ1=dФ' — изменение магнитного потока сквозь площадь, ограниченную контуром с током. Таким образом, dA=IdФ.(121.5) Проинтегрировав выражение (121.5), определим работу, совершаемую силами Ампера, при конечном произвольном перемещении контура в магнитном поле: (121.6) т. е. работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром. Формула (121.6) остается справедливой для контура любой формы в произвольном магнитном поле.

24. Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током. Закон Фарадея Согласно закону электромагнитной индукции Фарадея (в СИ): Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

25. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ

Прямолинейный проводник АВ движется в магнитном поле с индукцией В по проводящим шинам, которые замкнуты на гальванометр.

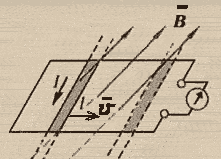
На электрические заряды, перемещающиеся вместе с проводником в магнитном поле, действует

сила Лоренца:

Fл = /q/vB sin a

Её направление можно определить по правилу левой руки.

Под действием силы Лоренца внутри проводника происходит распределение положительных и отрицательных зарядов вдоль всей длины проводника l.

Сила Лоренца является в данном случае сторонней силой, и в проводнике возникает ЭДС индукции, а на концах проводника АВ возникает разность потенциалов.

Причина возникновения ЭДС индукции в движущемся проводнике объясняется действием силы Лоренца на свободные заряды.

26. Явление самоиндукции заключается в появлении ЭДС индукции в самом проводнике при изменении тока в нем. Примером явления самоиндукции является опыт с двумя лампочками, подключенными параллельно через ключ к источнику тока, одна из которых подключается через катушку (рис. 39). При замыкании ключа лампочка 2, включенная через катушку, загорается позже лампочки 1. Это происходит потому, что после замыкания ключа ток достигает максимального значения не сразу, магнитное поле нарастающего тока породит в катушке индукционную ЭДС, которая в соответствии с правилом Ленца будет мешать нарастанию тока.

Для самоиндукции выполняется установленный опытным путем закон: ЭДС самоиндукции прямо пропорциональна скорости изменения тока в проводнике. .

Коэффициент пропорциональности L называют индуктивностью. Индуктивность — это величина, равная ЭДС самоиндукции при скорости изменения тока в проводнике 1 А/с. Единица индуктивности — генри (Гн). 1 Гн = 1 В • с/А. 1 генри — это индуктивность такого проводника, в котором возникает ЭДС самоиндукции 1 вольт при скорости изменения тока 1 А/с. Индуктивность характеризует магнитные свойства электрической цепи (проводника), зависит от магнитной проницаемости среды сердечника, размеров и формы катушки и числа витков в ней. При отключении катушки индуктивности от источника тока лампа, включенная параллельно катушке, дает кратковременную вспышку (рис. 40). 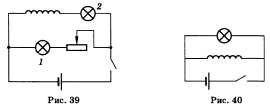Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки. Энергия магнитного поля находится по формуле . Энергия магнитного поля зависит от индуктивности проводника и силы тока в нем. Эта энергия может переходить в энергию электрического поля. Вихревое электрическое поле порождается переменным магнитным полем, а переменное электрическое поле порождает переменное магнитное поле, т. е. переменные электрическое и магнитное поля не могут существовать друг без друга. Их взаимосвязь позволяет сделать вывод о существовании единого электромагнитного поля. Электромагнитное поле — одно из основных физических полей, посредством которого осуществляется взаимодействие электрически заряженных частиц или частиц, обладающих магнитным моментом. Электромагнитное поле характеризуется напряженностью электрического поля и магнитной индукцией. Связь между этими величинами и распределением в пространстве электрических зарядов и токов была установлена в 60-х годах прошлого столетия Дж. Максвеллом. Эта связь носит название основных уравнений электродинамики, которые описывают электромагнитные явления в различных средах и в вакууме. Получены эти уравнения как обобщение установленных на опыте законов электрических и магнитных явлений.

27. Закон отражения света: падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α. Закон преломления света: падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред: Закон преломления был экспериментально установлен голландским ученым В. Снеллиусом в 1621 г. Постоянную величину n называют относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем преломления. Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления: n = n2 / n1. Законы отражения и преломления находят объяснение в волновой физике. Согласно волновым представлениям, преломление является следствием изменения скорости распространения волн при переходе из одной среды в другую. Физический смысл показателя преломления – это отношение скорости распространения волн в первой среде υ1 к скорости их распространения во второй среде υ2: Абсолютный показатель преломления равен отношению скорости света c в вакууме к скорости света υ в среде:

28. ЛИНЗЫ И ФОРМУЛЫ ЛИНЗ.

а) Типы линз.

Оптические линзы, которые в середине толще, чем на краю, называются собирающими; напротив, если край толще, чем середина, то линзы действуют как

рассеивающие. По форме поперечного сечения различают: двояковыпуклые, плоско-выпуклые, вогнуто-выпуклые собирающие линзы; двояковогнутые, плоско-вогнутые, выпукло-вогнутые рассеивающие линзы.

Тонкие линзы в первом приближении можно рассматривать как две сложенные тонкие призмы (рис.217, 218). Ход лучей можно проследить на шайбе Гартля.

Собирающая линза концентрирует параллельные лучи в одной точке за линзой, в фокусе (рис.219)

Рассеивающая линза превращает параллельный пучок лучей в расходящийся пучок, который кажется выходящим из фокуса (рис.220).

б) Построение изображения в линзах.

Для построения хода луча в линзе применяются те же законы, что и для вогнутого зеркала. Луч, параллельный оси, проходит через фокус и наоборот. Центральный луч (луч, идущий через оптический центр линзы) проходит через линзу без отклонения; в толстых линзах он немного смещается параллельно самому себе (как в плоскопараллельной пластинке, см. рис. 214). Из обратимости хода лучей следует, что каждая линза имеет два фокуса, которые находятся на одинаковых расстояниях от линзы (последнее верно лишь для тонких линз). Для тонких собирающих линз и центральных лучей справедливы следующие законы построения изображений:

g >2F; изображение обратное, уменьшенное, действительное, b >F (рис.221).

g = 2F; изображение обратное, равное, действительное, b = F.

F <g < 2F; изображение обратное, увеличенное, действительное, b > 2F.

g < F; изображение прямое, увеличенное, мнимое, - b > F.

При g < F лучи расходятся, на продолжении пересекаются и дают мнимое изображение. Линза действует как увеличительное стекло (лупа).

Изображения в рассеивающих линзах всегда мнимые, прямые и уменьшенные (рис.223).

в) Формула линзы.

Для тонких линз и центральных лучей применима

Формула линзы: 1/g + 1/b = 1/F = (n-1) · (1/r1 + 1/ r2).

Фокусное расстояние F зависит от коэффициента преломления стекла и радиусов кривизны линзы.

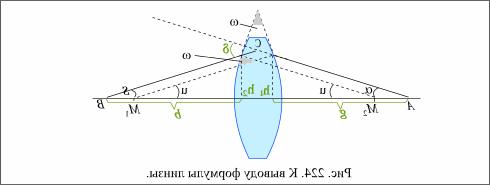
Вывод формулы (рис. 224): угол отклонения δ является внешним углом треугольника АВС:

δ = α + β; согласно закону тонких призм δ = (n-1) ω ; α ≈ tg α = h1/g ; β ≈ tg β = h2/b ;

и = sin и = h1/r1 ; v = sin v = h2/r2 ; и + v = ω .

После подстановки в выражении для δ получим:

h1/g + h2/b = (n-1) · (h1/r1 + h2/r2).

Для тонких линз h1 ≈ h2; следовательно,

1/g + 1/b = (n-1) · (1/r1 + 1/r2).

Оптическая сила измеряется в диоптриях. Оптическая сила является обратной величиной фокусного расстояния, измеренного в метрах.

D = 1/F м – 1.

Исправление недостатков зрения. При дальнозоркости лучи от предмета, попадая в глаз, пересекаются за сетчаткой. Собирающая линза, помещенная перед хрусталиком, приближает изображение, так что оно попадает на сетчатую оболочку. При близорукости лучи, слишком сильно преломленные глазом, не попадают на сетчатку. Рассеивающая линза делает их более расходящимися; тем самым изображение удаляется и попадает на сетчатку.

Микроскоп. Объектив – собирающая короткофокусная линза – дает обратное увеличенное действительное изображение маленького объекта (рис.227). Объект располагается вблизи фокуса; поэтому первое увеличение v1 = В1 / G = 1/F1. Окуляр помещается за изображением и действует подобно лупе. Второе увеличение

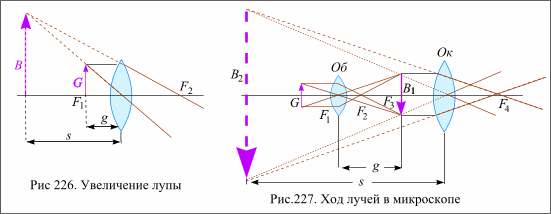
v2 = В2 / В1 = s / F2.; поэтому полное увеличение v = v1 v2 = ls / (F1 F2). Расстояние l равно приблизительно расстоянию между задним фокусом объектива и передним фокусом окуляра.

29. Плоские зеркала.

Закон отражения. Падающий луч, нормаль, т.е. перпендикуляр к отражающей

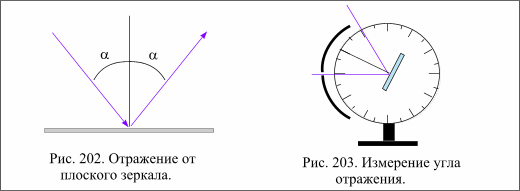
поверхности в точке падения, и отраженный луч лежат в одной плоскости (рис.202).

Угол падения равен углу отражения.

Доказательство при помощи шайбы Гартля.(рис.203): Вращающаяся горизонтальная щель пропускает узкий пучок света, который отражается от плоского зеркала, находящегося в центре шайбы. Отсчитывая положения светового пучка на градусной шкале диска, можно проверить закон отражения.

Выходящие из одной точки L лучи отражаются в плоском зеркале так, как будто они выходят из симметричной, по отношению к зеркалу, точки L΄ (рис.204). При отражении в плоском зеркале правая и левая стороны меняются местами.

Зеркала, расположенные под углом в 45º, служат для разметки прямых углов на местности (рис.205). и = 2α + 2β, α + β +135º = 180º, отсюда и = 90º.

Гладкие поверхности отражают падающие лучи только в одном направлении: правильное отражение (у «зеркальных поверхностей»).

Шероховатые поверхности отражают падающие лучи во всех направлениях: диффузное отражение. Вследствие диффузного отражения тела делаются видимыми; зеркало, которое полностью отражает, невидимо.

б) Сферические зеркала.

Небольшой участок поверхности сферического зеркала может рассматриваться как плоский; нормаль в точке падения совпадает с радиусом сферического зеркала. Лучи,

параллельные оптической оси, после отражения сходятся практически в одной точке F,

фокусе сферического зеркала(рис. 206, 207). Последний расположен посередине между центром сферы М и вершиной S вогнутого зеркала. Доказательство при помощи шайбы Гартля.

Фокусное расстояние F = r / 2.

Формула вогнутого сферического зеркала (рис.207). Расстояние предмета (светящейся точки G) от вершины S сферического зеркала обозначим буквой g, расстояние изображения В от S обозначим буквой b.

Формула вогнутого сферического зеркала :

1/g + 1/b = 1/ F.

Пояснение. На основании теоремы о биссектрисе угла в треугольнике имеем

GM : MB = GK : KB ≈ g : b для центральных лучей, падающих вблизи вершины зеркала S, (g – r) : (r – b) = g : b; gb – rb = gr – gb; 2gb = br + gr, деля на bgr, получаем:

2/r = 1/g + 1/b = 1/F, так как F = r/2.

Построение изображений в вогнутом зеркале: луч, параллельный оси зеркала, после отражения пройдет через фокус и обратно. Луч, проходящий через центр кривизны, отражается по той же нормали.

Величина предмета G относится к величине изображения В, как расстояние от предмета до центра зеркала к расстоянию от изображения до центра зеркала.

G : В = (g – r) : (r – b),

g > r : Изображение получается уменьшенным, обратным и действительным между центром М и фокусом F (рис.208).

g = r : Изображение равное, обратное, действительное в точке М.

F < g < r : Изображение увеличенное, обратное, действительное, b > r.

g < F : изображение увеличенное, мнимое ( кажущееся), прямое,

b < 0 – увеличительное зеркало (рис.209)

в) Выпуклые зеркала (рассеивающие).

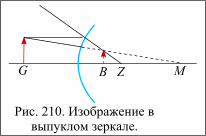
К сферическим выпуклым зеркалам применимы формулы вогнутых зеркал, только величине F надо приписать знак минус; в фокусе сходятся продолжения лучей, шедших параллельно оси зеркала и рассеянных зеркалом (рис.210)

Сферические выпуклые зеркала всегда дают, прямые, уменьшенные, мнимые изображения и обладают большим полем зрения.

г) Параболические зеркала.

Параболическое зеркало, в отличие от сферического собирает широкие параллельные пучки света точно в одной точке. Если источник света расположить в фокусе, то лучи после отражения становятся параллельными. Приближая источник света к вершине зеркала или удаляя его, можно сделать пучок лучей либо расходящимся, либо сходящимся.