1-Кулон установил,что 2 точечных заряда нах. в вакууме взаимодействуют друг с другом с силами определяемыми по формуле:

r-растояние между центрами точечных зарядов,E0=8.85*10 –электрическая постоянная.Если эти заряды нах. в некоторй среде,то сила взаимод.определяется по формуле:

Физ.величина показывающая во сколько раз сила Кулона в вакууме больше чем в данной среде наз. диэлектр. Проницаемостью среды.

-Закон сохранения эл. Заряда.Система зарядов является изолированной если при электрических процессах заряды могут переходить только между этими зарядами.В такой системе зарядов суммарный электр. заряд не изменяется при любых процессах происходящих при этих зарядах q1+q2+…=const

2    Если поочередно помещать в одну и ту же точку поля небольшие заряженные тела и измерять силы, то обнаружится, что сила, действующая на заряд со стороны поля, прямо пропорциональна этому заряду. Действительно, пусть поле создается точечным зарядомq₁. Согласно закону Кулона  на заряд q₂действует сила, пропорциональная заряду q₂. Поэтому отношение силы, действующей на помещаемый в данную точку поля заряд, к этому заряду для каждой точки поля не зависит от заряда и может рассматриваться как характеристика поля. Эту характеристику называют напряженностью электрического поля. Подобно силе, напряженность поля – векторная величина; ее обозначают буквой  . Если помещенный в поле заряд обозначить через q вместо q₂, то напряженность будет равна:  Напряженность поля в данной точке равна отношению силы, с которой поле действует на точечный заряд, помещенный в эту точку, к этому заряду.  Направление вектора   совпадает с направлением силы, действующей на положительный заряд, и противоположно направлению силы, действующей на отрицательный заряд  Напряженность поля точечного заряда. Найдем напряженность электрического поля, создаваемого точечным зарядом q₀. По закону Кулона этот заряд будет действовать на положительный заряд q с силой, равной

Модуль напряженности поля точечного заряда q₀ на расстоянии r от него равен

   :

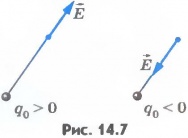
   Вектор напряженности в любой точке электрического поля направлен вдоль прямой, соединяющей эту точку и заряд (рис.14.7) и совпадает с силой, действующей на точечный положительный заряд, помещенный Принцип суперпозиции полей. Если на тело действует несколько сил, то согласно законам механики результирующая сила равна геометрической сумме этих сил:

если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых   и т. д., то результирующая напряженность поля в этой точке равна сумме напряженностей этих полей:

3 Поток вектора напряженности. Потоком вектора напряженности ,пронизывающим некоторую площадку s наз. величина находящаяся по формуле N=EScosl если во всех точках этой площадки напряженность одинаковая

4 Теорема Астр-Гаусса. Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

5Бесконечная равномерно заряженная нить

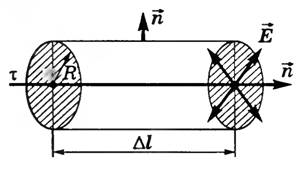
Линии напряженности электростатического поля, создаваемого нитью в сечении, перпендикулярном самой нити, направлены перпендикулярно боковой поверхности цилиндра, поэтому поток напряженности сквозь боковую поверхность N=E⋅2πRΔl, где R — радиус цилиндра. Через оба основания цилиндра поток напряженности равен нулю (α = 90°, cos α = 0). Тогда полный

поток напряженности через выделенный цилиндр

N=E⋅2πRΔl.

Заряд, находящийся внутри этого цилиндра, q = τ · Δl.

Согласно теореме Остроградского—Гаусса, можно записать  E⋅2πRΔl=

. Следовательно, модуль напряженности поля, создаваемого равномерно заряженной бесконечно длинной

нитью на расстоянии R от нее,

. 6Равномерно заряженная бесконечная плоскость

Пусть σ — поверхностная плотность заряда на плоскости

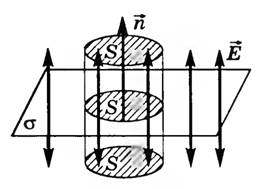
В качестве поверхности площадью S выберем цилиндрическую поверхность, образующая которой перпендикулярна плоскости. Основания этого цилиндра расположены перпендикулярно линиям напряженности по обе стороны от плоскости. Так как образующие цилиндра параллельны линиям напряженности (α = 90°, cos α = 0), то поток через боковую поверхность цилиндра отсутствует, и полный поток через поверхность цилиндра равен сумме потоков через два основания: N = 2ES. Внутри цилиндра заключен заряд q = σS, поэтому, согласно теореме Остроградского-Гаусса, 2ES=σS

7 Работа сил электрического поля.При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении равна A=FScosl=Eqscosl

8Электростатический потенциа́л (см. также кулоновский потенциал) — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля. Единицей измерения потенциала является, таким образом, единица измерения работы, деленная на единицу измерения заряда Потенциал φ в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку.

ЭКВИПОТЕНЦИА́ЛЬНАЯ ПОВЕ́РХНОСТЬ, поверхность, во всех точках которой потенциал электрического поля имеет одинаковое значение j= const. На плоскости эти поверхности представляют собой эквипотенциальные линии поля. Используются для графического изображения распределения потенциала.

Эквипотенциальные поверхности замкнуты и не пересекаются. Изображение эквипотенциальных поверхностей осуществляют таким образом, чтобы разности потенциалов между соседними эквипотенциальными поверхностями были одинаковы. В этом случае в тех участках, где линии эквипотенциальных поверхностей расположены гуще, больше напряженность поля.

Между двумя любыми точками на эквипотенциальной поверхности разность потенциалов равна нулю. Это означает, что вектор силы в любой точке траектории движения заряда по эквипотенциальной поверхности перпендикулярен вектору скорости. Следовательно, линии напряженности электростатического поля перпендикулярны эквипотенциальной поверхности. Другими словами: эквипотенциальная поверхность ортогональна к силовым линиям поля, а вектор напряженности электрического поля Е всегда перпендикулярен эквипотенциальным поверхностям и всегда направлен в сторону убывания потенциала. Работа сил электрического поля при любом перемещении заряда по эквипотенциальной поверхности равна нулю, так как ?j = 0. Эквипотенциальными поверхностями поля точечного электрического заряда являются сферы, в центре которых расположен заряд. Эквипотенциальные поверхности однородного электрического поля представляют собой плоскости, перпендикулярные линиям напряженности. Поверхность проводника в электростатическом поле является эквипотенциальной поверхностью.

9 Связь между напряженностью и разностью потенциалов

Установить связь меду напряженностью и разностью потенциалов для неоднородного поля можно, используя представление об эквипотенциальных поверхностях. Рассчитаем работу, совершаемую электрическим полем при перемещении электрического заряда с одной эквипотенциальной поверхности на соседнюю по направлению нормали к этой поверхности (рис. 1.27). Если расстояние между поверхностями по нормали настолько мало, что на этом участке можно считать поле однородным, то можно записать выражение для элементарной работы через напряженность поля и расстояние между эквипотенциальными поверхностями:

10Емкость плоского конденсатора.

т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.

Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники наз. обкладками конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок.

11. Характеристики электрического тока

Сила и плотность тока

Силой тока называется физическая величина, равная отношению количества заряда, прошедшего за некоторое время через поперечное сечение проводника, к величине этого промежутка времени.

Сила тока в Международной системе единиц (СИ) измеряется в амперах.

По закону Ома сила тока I для участка цепи прямо пропорциональна приложенному напряжению U к участку цепи и обратно пропорциональна сопротивлению R проводника этого участка цепи :

Плотностью тока называется вектор, модуль которого равен отношению силы тока, протекающего через некоторую площадку, перпендикулярную направлению тока, к величине этой площадки, а направление вектора совпадает с направлением движения положительного заряда в токе.

Согласно закону Ома плотность тока в среде j пропорциональна напряжённости электрического поля E и проводимости среды :

Мощность

При наличии тока в проводнике совершается работа против сил сопротивления. Эта работа выделяется в виде тепла. Мощностью тепловых потерь называется величина, равная количеству выделившегося тепла в единицу времени. Согласно закону Джоуля — Ленца мощность тепловых потерь в проводнике пропорциональна силе протекающего тока и приложенному напряжению:

Мощность измеряется в ваттах

В сплошной среде объёмная мощность потерь p определяется скалярным произведением вектора плотности тока j и вектора напряжённости электрического поля E в данной точке:

Объёмная мощность измеряется в ваттах на кубический метр.

12.Электродвижущая сила.

Если два тела А и В , находящиеся под разными потенциалами соед. проводником А и В то по нему потечет ток, который через короткое время, когда потенциально уравняются, прекратится.

Для поддержания неизменного по времени тока необходимо поддерживать неизменной разность потенциалов, f1-f2 -соnst т.е. все время пополнять заряды соединенных тел .Это

можно сделать только перенося заряды обратно в тело А, введя как бы круговорот электричества, для чего контур по которому идет ток, должен быть замкнут (АаВbА)

Однако на участке ВbА зарядам придется перемещаться против электрических сил. Это перемещение могут совершать лишь сторонние силы, которче могут действовать либо на всем

протяжении цепи, либо на отдельных ее участках.

Электродвижущая сила (ЭДС) источника тока – Величина, равная отношению работы, которую совершают сторонние силы при перемещении точечного положительного заряда вдоль всей цепи, включая и источник тока, к заряду.

Единица ЭДС – вольт (В)

16. Закон Ома для полной цепи.

Расмотрим замкнутую цепь, состоящую из внешней части, имеющей сопротивление R , и внутренней – источника тока сопротивление которого r .

Согласно закону сохранения энергии ЭДС источника тока равна сумме падений напряжений как внешней и внутренних участках цепи, так как при перемещении по замкнутой цепи, так как при перемещении по замкнутой цепи заряд возвращается в исходное положение с тем же потенциалом ( т.е.f b = f a)Сила тока в цепи пропорционально действующей в цепи ЭДС и обратно пропорциональна сумме сопротивления цепи и внутреннего сопротивления источника

(Закон Ома для полной цепи)

Формулой можно воспользоваться только тогда, когда ток идет внутри источника от отрицательного полюса к положительному , а во внешней цепи – от положительного к отрицательному.

13.Закон ома для участка цепи. Сопротивление проводников

где U - напряжение на концах участка цепи, R - сопротивление участка цепи. (сам проводник тоже можно считать участком цепи).

Для каждого проводника существует своя определенная вольт-амперная характеристика.

СОПРОТИВЛЕНИЕ

- основная электрическая характеристика проводника.

- по закону Ома эта величина постоянна для данного проводника.

1 Ом - это сопротивление проводника с разностью потенциалов на его концах

в 1 В и силой тока в нем 1 А.

Сопротивление зависит только от свойств проводника:

где S - площадь поперечного сечения проводника, l - длина проводника,

ро - удельное сопротивление, характеризующее свойства вещества проводника.

14. Закон ома в дифференциальной форме. Плотность тока

Друде считал, что сразу после очередного соударения электрона с ионом кристаллической решетки скорость упорядоченного движения электрона равна нулю. Предположим, что напряженность поля не изменяется. Тогда под действием поля электрон получит постоянное ускорение равное

и к концу пробега скорость упорядоченного движения достигнет значения

(18.2)

где t - среднее время между двумя последовательными соударениями электрона с ионами решетки. Друде не учитывал распределение электронов по скоростям и приписывал всем электронам одинаковое значение средней скорости . В этом приближении , где - среднее значение длины свободного пробега, - скорость теплового движения электронов. Подставим это значение t в формулу (18.2)

Скорость изменяется за время пробега линейно. Поэтому ее среднее (за пробег) значение равно половине максимального

Подставив это выражение в

получим

Плотность тока оказалась пропорциональной напряженности поля. Следовательно, мы получили закон Ома. Согласно коэффициент пропорциональности между j и Е представляет собой проводимость

(18.3)

Если бы электроны не сталкивались с ионами решетки, длина свободного пробега, а, следовательно, и проводимость были бы бесконечно велики. Таким образом, электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами.