Билет 7

1.Тормозное рентгеновское излучение.

Рентгеновское излучение возникает при бомбардировке твердых мишеней быстрыми электронами (рис. 2.6) Здесь анод выполнен из W, Mo, Cu, Pt – тяжелых тугоплавких или с высоким коэффициентом теплопроводности металлов.

Начальная скорость электрона :

Согласно классической электродинамике при торможении электрона должны возникать излучения всех длин волн от нуля до бесконечности. Длина волны, на которую приходится максимум мощности излучения, должна уменьшиться по мере увеличения скорости электронов

О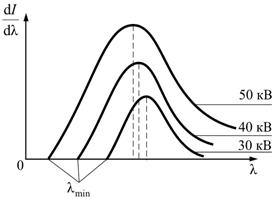 днако есть принципиальное отличие от классической теории: нулевые распределения мощности не идут к началу координат, а обрываются при конечных значениях – это и есть коротковолновая граница рентгеновского спектра.

; ;

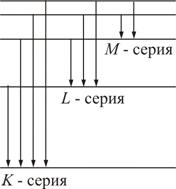
Характеристическое рентгеновское излучение.

Когда энергия бомбардирующих анод электронов становится достаточной для вырывания электронов из внутренних оболочек атома, на фоне тормозного излучения появляются резкие линии характеристического излучения. Частоты этих линий зависят от природы вещества анода, поэтому их и назвали характеристическими.   Все переходы на k-оболочку образуют K-серию, соответственно, на l- и m-оболочки – L- и M-серии

  Английский физик Генри Мозли в 1913 году установил закон, названный его именем, связывающий частоты линий рентгеновского спектра  с атомным номером испускающего их элемента Z: ,  , где k = 3, 4, 5…; n=k+1,k+2,k+3… .

Чем дальше электрон от ядра, тем σ больше.

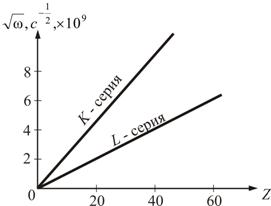  Закон Мозли позволил по измерению длин волн λ рентгеновских лучей точно установить атомный номер элемента. Он сыграл большую роль при размещение элементов в таблице Менделеева.

2. Сложение колебаний, происходящих в одном направлении.

Пусть точка одновременно участвует в двух гармонических колебаниях одинакового периода, направленных вдоль одной прямой.

Сложение колебаний будем проводить методом векторных диаграмм (рис. 2.2). Пусть колебания заданы уравнениями

и

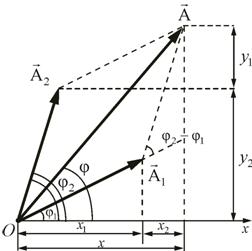
  Рассмотрим несколько простых случаев.

       1.     Разность фаз равна нулю или четному числу π, то есть   , где   . Тогда    и

 так как   , т.е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний (колебания синфазны) 

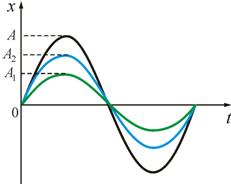
2.Разность фаз равна нечетному числу π, то есть   , где   . Тогда   . Отсюда

      На рис. 2.4 изображена амплитуда результирующего колебания А, равная разности амплитуд складываемых колебаний (колебания в противофазе).

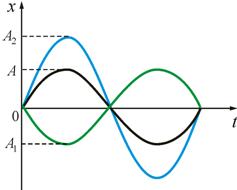
3. Теплоемкость при постоянном давлении и объеме.

Особый интерес представляют средние и истинные теплоемкости в процессах при постоянном объеме   (изохорная теплоемкость, равная отношению удельного количества теплоты в изохорном процессе к изменению температуры рабочего тела dT) и при постоянном давлении   (изобарная теплоемкость, равная отношению удельного количества теплоты в изобарном процессе к изменению температуры рабочего тела dT).

Для идеальных газов связь между изобарной и изохорной теплоёмкостями и устанавливается известным уравнением Майера  .

Из уравнения Майера следует, что изобарная теплоемкость больше изохорной на значение удельной характеристической постоянной идеального газа. Это объясняется тем, что в изохорном процессе ( ) внешняя работа не выполняется и теплота расходуется только на изменение внутренней энергии рабочего тела, тогда как в изобарном процессе ( ) теплота расходуется не только на изменение внутренней энергии рабочего тела, зависящей от его температуры, но и на совершение им внешней работы.

Д ля реальных газов  , так как при их расширении и   совершается работа не только против внешних сил, но и внутренняя работа против сил взаимодействия между молекулами газа, на что дополнительно расходуется теплота.

В теплотехнике широко применяется отношение теплоемкостей  , которое носит название коэффициента Пуассона (показателя адиабаты).

Теплоемкости   и   зависят от температуры, следовательно, и показатель адиабаты   должен зависеть от температуры.

Известно, что с повышением температуры теплоёмкость   увеличивается. Поэтому с ростом температуры   уменьшается, приближаясь к единице. Однако всегда остается больше единицы. Обычно зависимость показателя адиабаты от температуры выражается формулой вида

,

где   - значение коэффициента при 0⁰ С;   - коэффициент, принимающий для каждого газа своё постоянное значение.

Кроме того, можно установить следующие широко использующиеся зависимости.

,

(2.8)

и так как 

.