45. Какие упрощающие предположения использованы в лабораторной работе №10?

, (2)

В нашей установке I >> I’ , поэтому формула (2) упрощается:

I – момент инерции маятника,

I’– момент инерции тела относительно оси маятника

(3)

Пренебрегая потерями на трение в установке, закон сохранения механической энергии маятника, после попадания в него снаряда, можно записать в виде:

(4)

где – кинетическая энергия маятника сразу после соударения,

- потенциальная энергия упругой деформации в момент максимального угла поворота маятника, k - модуль кручения нити, - ₀ максимальный угол поворота маятника.

46. Что такое вязкость? Дайте определение вязкости, укажите единицу измерения.

Вязкость (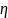 ) – численно равна силе вязкого трения между слоями жидкости, движущимися параллельно друг другу, действующая на единицу поверхности при единичном градиенте скорости.

Единицы измерения: СИ: [ ]=кг/м*с=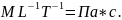

СГС: [ ]=г/см*с=Пз

Единица измерения 1 Пз – пуаз, назван в честь французского ученого Ж. Пуазеля, исследовавшего в 1840 г. течение вязкой жидкости.

47. ОТ каких величин зависит вязкость.

Вязкость зависит от природы и свойств жидкости, температуры и однородности среды. С повышением температуры вязкость жидкости уменьшается.

48. Какие силы действуют на шарик, падающий в жидкости в лабораторной работе номер 11 «Определение коэффициента внутреннего трения по методу Стокса»?

На шар, падающий в жидкости, действуют 3 силы:

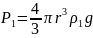– сила тяжести;

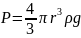– выталкивающая сила Архимеда;

.

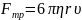r – радиус шара;

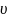– скорость движения шара;

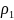– плотность шара;

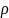- плотность жидкости;

- вязкость жидкости;

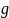– ускорение свободного падения.

49. Почему в лабораторной работе номер 11, начиная с определенного момента движение шара становится равномерным?

После того, как с начала движения пройдет время, равное 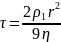– релаксационный период движения шара, шар будет двигаться с постоянной скоростью, т.к. силы, действующие на шар, будут уравновешиваться, а течение станет

50. Каким образом можно было бы в лабораторной работе номер 14 учесть тот факт, что блок обладает массой?

В случае учета массы блока, натяжения нитей по обе стороны блока будут различными. Если нить считать невесомой и нерастяжимой (что тоже является упрощением), система уравнений принимает вид:

,

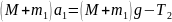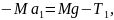
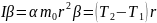
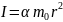– момент инерции блока относительно центра масс;

– коэффициент, зависящий от распределения массы в блоке;

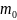- масса блока;

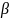- угловое ускорение;

- радиус блока.

№51

В гидродинамике для удобства расчетов вводятся понятия линии тока и трубки тока.

Линия, касательная к которой в любой точке указывает направление скорости частицы жидкости, проходящей в рассматриваемый момент времени через точку касания, называется линией тока.

В движущейся жидкости возьмем произвольный замкнутый контур С и через точки его в один и тот же момент времени проведем линии тока. Совокупность линий тока, проведенных через все точки контура С, образуют трубчатую поверхность, называемую трубкой тока.

Если поперечное сечение трубки тока бесконечно мало, то можно считать, что скорость жидкости постоянна по сечению и направлена вдоль оси трубки тока. Масса жидкости, протекающая за время 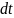через поперечное сечение трубки, определяется выражением:

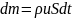, где:

– плотность жидкости;

u –скорость жидкости;

S – площадь нормального сечения трубки тока.

В случае стационарного течения масса жидкости, протекающая в единицу времени через любые сечения данной трубки тока, будет одной и той же. Если взять два сечения трубки, площади которых равны 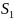и 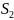,то можно написать:

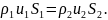
Эта формула выражает один из основных законов гидродинамики – закон сохранения массы или уравнения неразрывности.

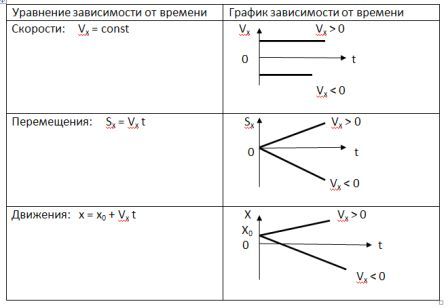
№ 52

График зависимости от времени ускорения, скорости и пути при равномерном прямолинейном движении

№ 53

Цена деления – значение измеряемой величины, которая приходится на одно деление шкалы прибора

№54

Закон сохранения импульса : импульс замкнутой системы материальных точек остается постоянным

№ 55

Если шар движется с малой скоростью (безвихревое движение) в неограниченной стенками жидкости, то сила сопротивления, обусловленная силами внутреннего трения, согласно закону Стокса, равна:

.

Если шар движется не в неограниченной жидкости, а в сосуде с конечным поперечным сечением, тогда нужно учесть влияние стенок надвижение шара. Если радиус цилиндрического сосуда равен R, то сила сопротивления движению шара равна

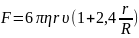
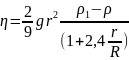
при движении шара в жидкости(или, наоборот, при обтекании неподвижного шара) характерной скоростью является скорость шара (или, соответственно, средняя скорость жидкости), а характерным размером – диаметр шара