4 Виды распределений, наиболее часто используемые при обработке результатов измерений.
В процессе обработки результатов измерений используются различные виды закона распределения (нормальный закон распределения, равномерный закон распределения корреляционный закон распределения) измеряемой величины (в данном случае она рассматривается как случайная).
При обработке результатов измерений приходится встречаться с различными законами распределения измеряемых величин, рассматриваемых как случайные величины: нормальный закон распределения, равномерный закон распределения, арксинусный закон распределения, треугольный закон распределения, корреляционный закон распределения.
ВИДЫ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИ
2.2.1 Нормальный зрсв (нзрсв)
Н
ЗРСВ
характерен для случайных процессов,
согласно центральной предельной теореме,
причиной которого является наличие
множества независимых, случайных,
слабовыраженных факторов.
(2.11) Рисунок 2.4
(2.12),
при
,
соответствует
точке перегиба графика
,
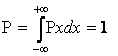ограничивающей область НЗРСВ, в которую
попадает большая часть погрешностей.
.
(2.13)
Вероятность
попадает в интервал (
)
равна приблизительно 2/3.
В
ероятность
попадания в интервал, ограниченный
значением погрешности, соответствующей
значению 3-х сигм равна:
.
(2.14)
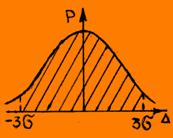
Рисунок 2.5
З
акон
3-х сигм определяет границы учитываемых,
при расчетах, результатов измерений.
Погрешности, превышающие значение |3
|,
считаются грубыми погрешностями
(промахами). Пятидесятипроцентной
вероятности (Р = 0,5) соответствует интервал
неопределенности равный:
Общая характеристика НЗРСВ:
Рассеяние результатов симметрично относительно математического ожидания, т.е. вероятности появления положительных и отрицательных отклонений приблизительно равны.
Вероятность появления малых погрешностей значительно выше вероятности появления больших погрешностей.
Среднее арифметическое результатов многократных измерений практически постоянно.
При n < 20 экспериментальный ЗРСВ точнее отражается распределением Стьюдента и может существенно отличаться от НЗРСВ.
Рисунок 2.6 , (2.15)
где k = n - 1 - число степеней свободы;
t - коэффициент Стьюдента.
При малом числе
измерений (n <20)
,
где Sx
– статистическая оценка СКО,
теоретическое
значение СКО существенно отличается
от статистической оценки СКО.
.
(2.16)
При статистической оценке СКО находится путем деления суммы квадратов остаточных отклонений на (n - 1), т.к. число степеней свободы уменьшается на 1, потому что:
M[x]
,
тогда:
и
.
(2.17)
2.2.2 Равномерный закон распределения случайных величин
По этому закону распределяются случайные составляющие погрешности измерений, обусловленные «сухим» трением, погрешности округления отчетов по шкале, погрешности квантования аналого-цифрового преобразователя.
Рисунок 2.7
d = 2a – энтропийная оценка неопределенности измерения.
Первый начальный момент равномерного ЗРСВ равен:
,
(2.18)
Первый центральный момент равен нулю:
,
(2.19)
,
,
При равномерной плотности вероятности:
,
второй центральный момент соответствует дисперсии и равен:
.
(2.20)
При этом СКО можно определить по формуле:
.
Третий центральный момент и коэффициент асимметрии равны нулю:
kассим=
.
(2.21)
Четвертый центральный момент и эксцесс, соответственно:
(2.22)