26 Основные постулаты метрологии

Постулаты:

1. У измеряемой величины есть истинное значение.

2. Истинное значение величины определить невозможно.

3. Истинное значение измеряемой величины постоянно.

Пояснение: В рамках принятой модели объекта исследования существует определенная физическая величина и ее истинное значение. Если считать, что деталь представляет собой цилиндр (модель – цилиндр), то она имеет диаметр, который может быть измерен. Если же деталь нельзя считать цилиндрической, например, ее сечение представляет собой эллипс, то измерять ее диаметр бессмысленно, поскольку измеренное значение не несет полезной информации о детали. И, следовательно, в рамках новой модели диаметр не существует. Измеряемая величина существует лишь в рамках принятой модели, то есть имеет смысл только до тех пор, пока модель признается адекватной объекту. Так как при различных целях исследований данному объекту могут быть сопоставлены различные модели,то для данной физической величины объекта измерения существует множество измеряемых величин (и соответственно их истинных значений)(истинное значение определить невозможно). Измеряемому свойству объекта измерений должен соответствовать некоторый параметр его модели. Данная модель в течение времени, необходимого для измерения, должна позволять считать этот параметр неизменным. В противном случае измерения не могут быть проведены. Указанный факт описывается –истинное значение измеряемой величины постоянно.

27 Оценка динамической погрешности

Статическая погрешность измерений - погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей.

Динамической называют погрешность, зависящую от скорости изменения измеряемой величины во времени. Возникновение динамической погрешности обусловлено инерционностью элементов измерительной цепи средства измерений. Динамической погрешностью средства измерений является разность между погрешностью средства измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.

Для цифровых измерений принципиальное значение имеет выбор частоты дискретизации переменных величин. Самая грубая оценка частоты дискретизации выполняется по теореме Котельникова. Она позволяет выделить все спектральные составляющие сигнала, если для максимальной частоты на период приходится не менее двух значений оцифровки. При этом погрешность в определении амплитуды каждой из спектральных составляющих будет разной для разных частот.

Для оценки погрешности в зависимости от частоты оцифровки можно пользоваться следующим приемом. Пусть измеряемая величина имеет вид, показанный на рисунке

В простейшем случае для восстановления функции дискретные отсчеты соединяются прямыми линиями. Погрешность определяется кривизной кривой . Если кривизну описать параболой, то

,

где - вторая производная от ; - период дискретизации.

Если приведенная погрешность , где - диапазон изменения , то

Для синусоидального сигнала . Откуда для спектральных составляющих

или число отсчетов на период

Для оценки числа n можно пользоваться таблицей

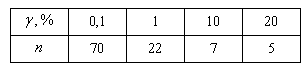
Таким образом, можно оценить необходимый период дискретизации или число дискретных отсчетов n на период, необходимых для восстановления с нужной точностью спектральных составляющих сигнала.

Таким образом, при цифровой обработке сигнала короткие (импульсные) сигналы значительно искажаются при недостаточной частоте дискретизации. Особенно это проявляется, когда в сигналах присутствуют острые пики или резкие фронты, которые имеют вид или функций с бесконечно широким спектром.

Грубая оценка динамической погрешности при аналоговой регистрации. Пусть квазистатический регистрирующий прибор имеет амплитудно-частотную характеристику, которая представлена на рисунке

Здесь - зависимость чувствительности от частоты, соответствует погрешности, определяющей граничную частоту измерений .

Зависимость погрешности от частоты может быть вычислена по формуле

,

где - резонансная частота прибора. Формула предполагает, что вершина резонансной кривой может быть приближенно описана перевернутой параболой.

Таким же образом оценивается частотная погрешность для непериодических процессов.

Например, термопара и термометр могут быть представлены апериодическим звеном первого порядка. Тогда

,

где ; - постоянная времени.

То есть для периодических и непериодических процессов динамическая погрешность зависит от характерных времени или частоты изменения измеряемой величины.

Математически легче описываются синусоидальные. К несинусоидальным относятся: шумы, помехи, наводки (описание которых затруднено).

В тетради:

1. СИ аналоговые, АЧХ апериодическая (термопары, реостатный датчик); про это сказано выше (грубая оценка динамической погрешности при аналоговой регистрации);

2. Система с собственными колебательными звеньями с малым успокоением (это в тетради, у меня нет сканера, там немножечко другой график).

,

где - коэффициент успокоения.