Лекция 2 Погрешности измерений

Основным показателем точности измерений является погрешность – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность выражается в абсолютной или относительной форме. Абсолютная погрешность определяется как разность между измеренным и действительным значением измеряемой величины:

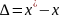
Где Δ – абсолютная погрешность, x – действительное значение, x* - измеренное значение.

Относительная погрешность определяется как отношение абсолютной погрешности к действительному значению измеряемой величины:

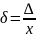
Существует также приведенная погрешность, которая равняется отношению абсолютной погрешности к максимальному значению измеряемой величины:

Абсолютная погрешность выражается в единицах измерения физических величин, а относительная и приведенная выражаются или в процентах, или в относительных единицах.

При анализе погрешностей выделяют отдельные составляющие погрешности, которые систематизируются по различным признакам.

1. По источнику возникновения погрешности:

- методические;

- инструментальные;

- личностные (личные);

Так как результат измерений состоит из метода, средств труда (инструмент) и личности, которая проводит эксперимент. Несовершенство каждой из этих составляющих вносит погрешность.

2. По способу проявления погрешности подразделяются на:

- случайные;- систематические. Систематической погрешностью принято называть составляющую погрешности измерения, которая остается постоянной или изменяется по известному закону при повторных измерениях. В соответствии с этим определением погрешности разделяются на постоянные и переменные, а переменные, в свою очередь, подразделяются на прогрессирующие, периодические и изменяющиеся по сложному закону (рис 2.1).

П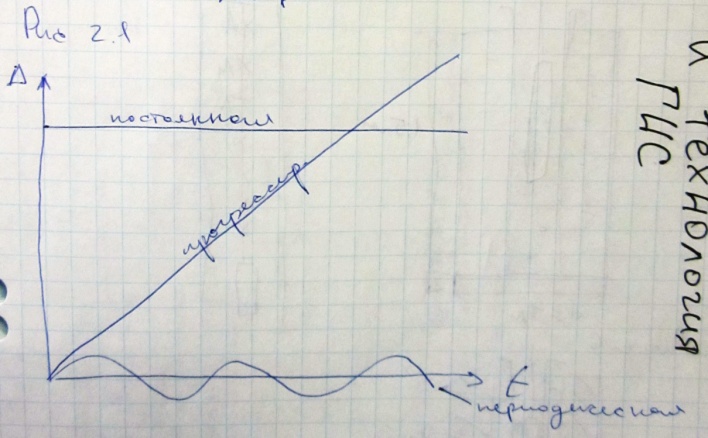 остоянные остаются неизменными в течение всей серии измерений (погрешности из индивидуальных особенностей средств измерений из-за неточной передачи размера единиц измерений от образцовой меры).

Переменные систематические погрешности изменяются в процессе измерений. Могут быть вызваны гармоничными колебаниями или изменениями напряжений в сети. Например, на буровых установках стоят свои генераторы и стабилизаторы не всегда могут поддержать ток неизменным.

Влияние систематических погрешностей может быть сведено к минимуму путем сохранения постоянных условий измерения, а также посредством введения поправок. Зная закон изменения погрешностей, мы можем ввести поправку. Второй способ учета – это выполнение измерений в контрольных скважинах и сравнение результатов с образцовыми кривыми. Если есть расхождение и можно определить закон его изменения, погрешность нужно учитывать.

Случайная погрешность – это составляющая погрешности, изменяющаяся случайным образом при измерении одной и той же величины. Ее нельзя учесть при обработке и случаях, если она превышает допустимые пределы, результаты измерений бракуются.

Кроме систематических и случайных погрешностей встречаются грубые погрешности, иногда называемые промахами. Их источниками могут быть как личностные факторы (оператора), так и другие, например, резкие колебания напряжения в питающей сети.

Грубые погрешности выявляются в процессе обработки результатов измерений и соответствующе измерения исключаются из обработки.

Рассматривая более детально систематическую погрешность, можно выделить еще две составляющих:

1) аддитивная. Значение аддитивной погрешности в каждой точке шкалы постоянное;

2) мультипликативная. Погрешность, которая линейно возрастает или убывает с ростом измеряемой величины.

И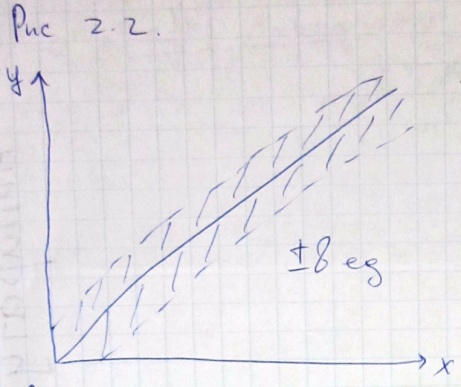 зобразить их можно, как на рис 2.2. Допустим, в каждой точке аддитивная погрешность добавляет 8 единиц. На рис 2.3. мультипликативная составляющая, т.е. чем больше значение измеряемой величины, тем больше погрешность.

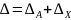
Где - аддитивная погрешность; – мультипликативная погрешность.

И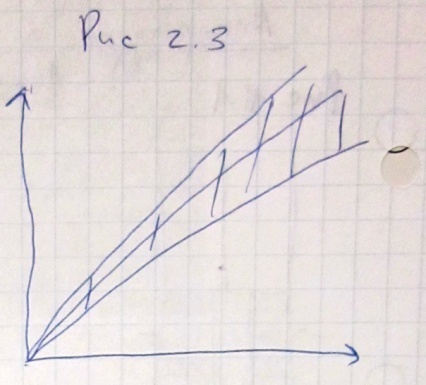 ногда аддитивную погрешность называют погрешностью нуля, потому что измерение может быть равно нулю, а погрешность уже есть. Примером мультипликативной погрешности можно привести измерения БК.

Где k – коэффициент зонда в метрах. Если неправильно определим коэффициент, то будем вносить мультипликативную погрешность. Есть способ превратить мультипликативную погрешность в аддитивную. Прологарифмируем выражение:

Теперь получили аддитивную погрешность, которая будет сдвигаться от истинного значения на k. Кривые бокового каротажа выводятся в логарифмическом масштабе.