2) Переход в пространстве от старой системы координат к новой с тем же началом. Общее преобразование одск в пространстве.

Если векторы базиса в базисе имеют разложение

т.е. матрица перехода имеет вид:

,

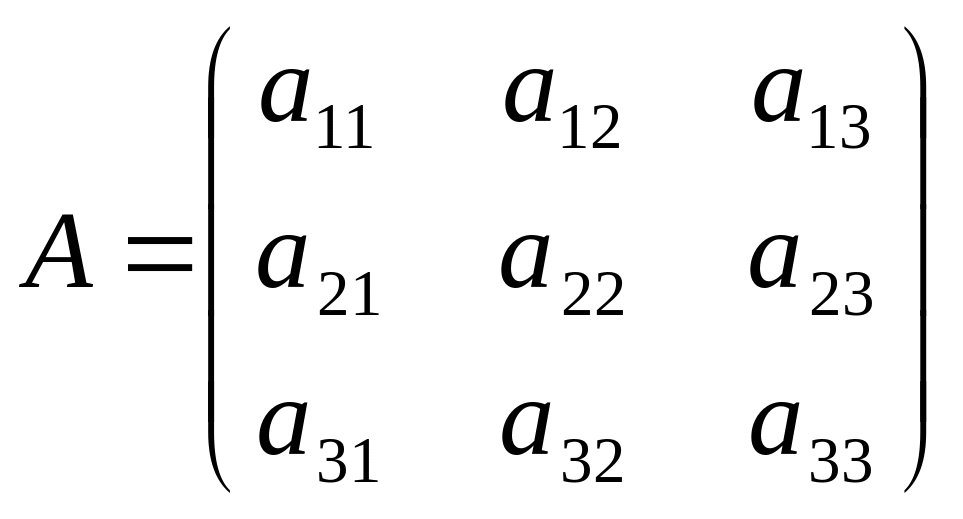то аналогично плоскому случаю связь между старыми координатами (x, y, z) точки M и новыми(x’, y’, z’) имеет вид:

При общем же преобразовании ОДСК в пространстве, объединяя формулы (1) и (2), получаем связь в виде:

,

где - координаты начала новой системы координат в старой, A(i, j) – элементы матрицы перехода, составляемой из координат векторов в базисе ( ).

БИЛЕТ №20. «Преобразование ДПСК в пространстве»

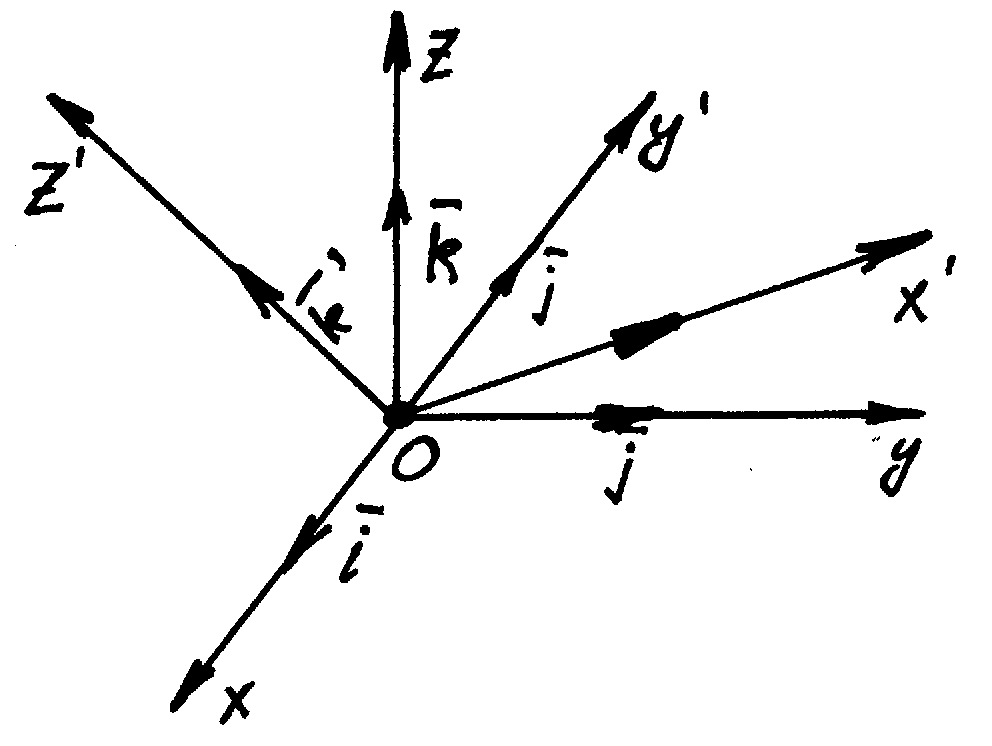
Т.к. в ДПСК все масштабные векторы имеют одинаковую длину, то координатами векторов в базисе являются направляющие косинусы этих векторов, т.е. косинусы углов, которые эти вектора образуют с осями Ox, Oy и Oz:

Тогда связь между старыми координатами и новыми при переходе от одной ДПСК к другой будет иметь вид:

а связь при общем преобразовании ДПСК примет вид:

Рассмотрим матрицу перехода от старой системы координат к новой:

Как и в случае плоского случая ДПСК определитель этой матрицы равен в зависимости от того, имеет старая и новая системы координат одну и ту же либо противоположную ориентации. Кроме того, как и в плоском случае, скалярное произведение двух различных строк (столбцов) равно нулю, а скалярное произведение строки (столбца) на себя равно 1. Такие матрицы называются ортогональными, как и преобразования, определяемые ими. Рассмотрим отдельно матрицу перехода от старой системы координат к новой, получающейся из старой ДПСК поворотом вокруг оси Oz на угол . При таком преобразовании изменяются лишь первые две координаты точки. (Связь между ними для плоского случая известна). Тогда связь между старыми и новыми координатами будет иметь вид:

A=

Координаты векторов при преобразовании системы координат в пространстве изменяются аналогично плоскому случаю.

БИЛЕТ №21. “Углы Эйлера»

Рассмотрим переход от одной ДПСК к другой с одним и тем же началом O. Матрица перехода имеет вид:

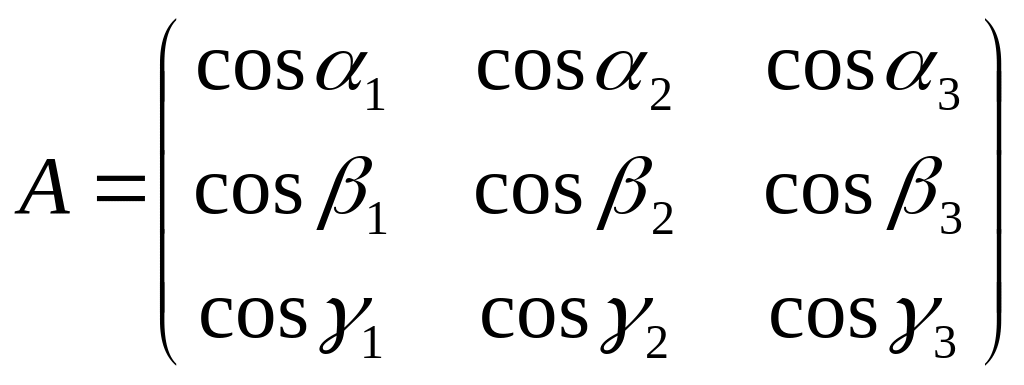
и содержит 9 элементов, которые связаны между собой шестью соотношениями:

Таким образом, 3 параметра определяются произвольно. Эйлер показал, что рассматриваемые преобразования можно представить в виде трех последовательных поворотов вокруг исходной оси координат и вспомогательных осей на углы EMBED Equation.3 , называемые углами Эйлера.

Т.к. плоскости XOY и X’OY’ имеют общую точку O, то они имеют и общую прямую, по которой мы направим ось . Перейдем от системы координат OXYZ к системе , где ось перпендикулярна плоскости и направлена таким образом, что система координат OXYZ и имеют одну и ту же ориентацию:

I. OXYZ

II.

Т.к. системы I и II имеют общую ось z, то система II получается поворотом системы I вокруг оси z на неполный угол и связь между координатами системы I и II имеет вид:

От системы II перейдем к системе III.

III. . Оси и z’ перпендикулярны, т.к. z’ перпендикулярна X’OY’, в которой лежит ось , а ось перпендикулярна плоскости и направлена таким образом, чтобы система координат III имела ту же самую ориентацию, что и системы I и II.

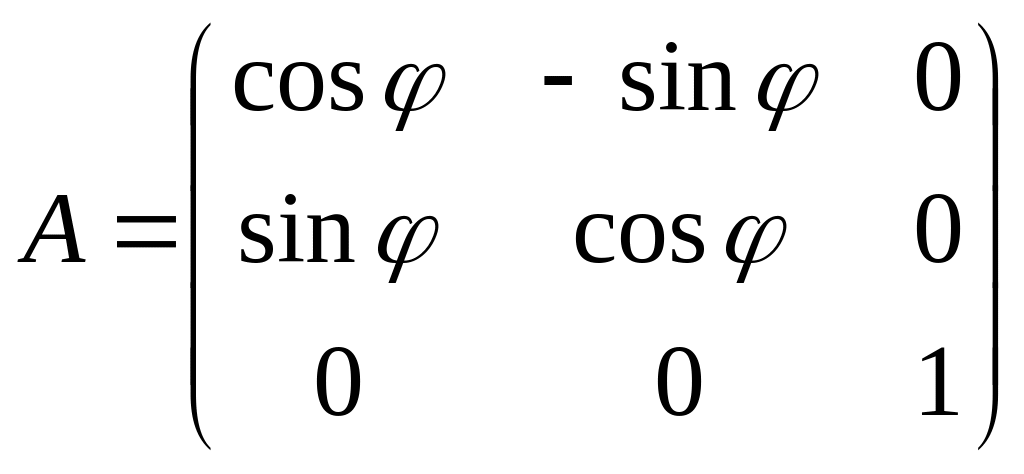
Связь между старыми и новыми координатами при переходе от системы II к системе III, т.е. при повороте относительно оси имеет вид:

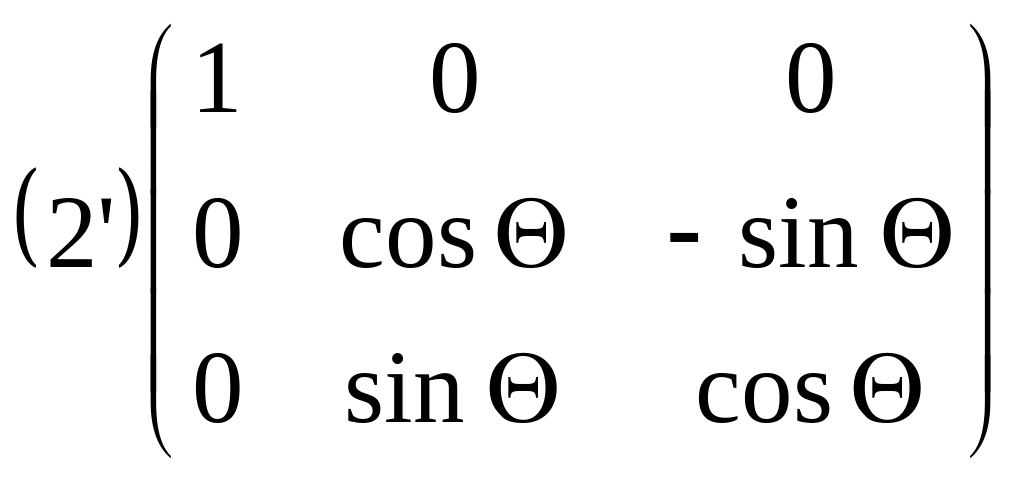
От системы III перейдем к системе OX’Y’Z’ с помощью поворота вокруг оси z’.

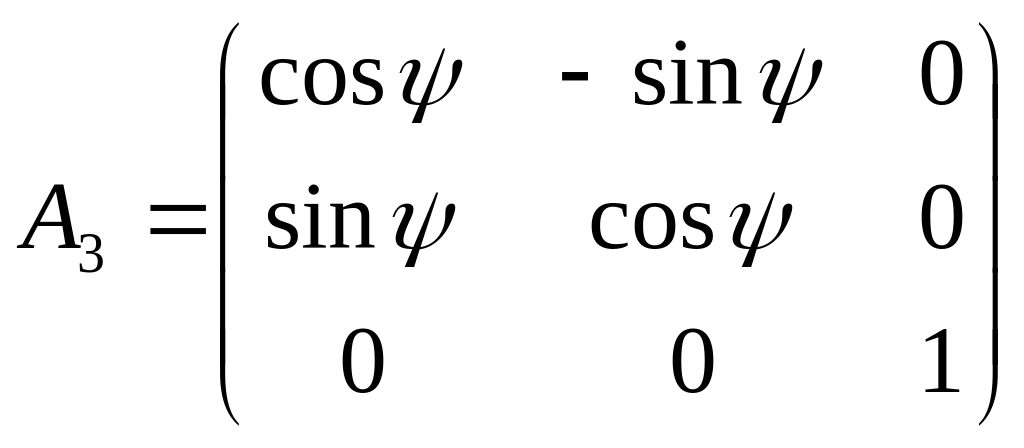
Т.к. эти преобразования ортогональны, то результирующее преобразование – переход от XOYZ к X’OY’Z’ – также ортогонально. Углы , на которые осуществляется поворот, называются углам Эйлера. Найдем связь между старыми координатами точки (x, y, z) и новыми (x’, y’, z’) через углы Эйлера. Для этого подставим (3) в (2), а (2) в (1):

Таким образом, в соотношения входят тригонометрические функции трех углов Эйлера.

БИЛЕТ №22. «Полярные системы координат».

1) Полярная система координат на плоскости. Полярной системой координат ориентированной плоскости называется точка 0 – полюс системы координат, луч, выходящий из этой точки и выбранный на нем масштабный отрезок, т.е. полярная ось. Полярными координатами точки M на плоскости называется упорядоченная пара , где r – расстояние от полюса до точки, а - угол, который образует радиус-вектор с полярной осью.

Замечание. При построении кривых второго порядка обычно используются обобщенные полярные координаты, в которых первая координата r может принимать и отрицательные значения.

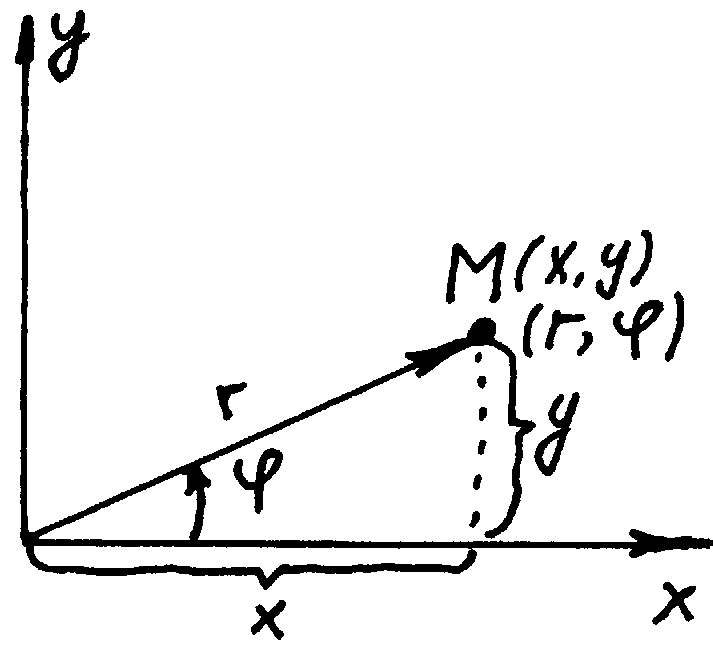
Установим связь между ДПСК на ориентированной плоскости и ее полярными координатами. Для этого на плоскости введем ДПСК так, чтобы ее начало O совпадало с полюсом полярной системы, ось абсцисс была направлена по полярной оси, ось Oy была перпендикулярна ей и направлена так, чтобы в соответствии с ориентацией плоскости угол между Ox и Oy равнялся 90^o и масштабные векторы, построенные в ДПСК имели ту же длину, что и в полярной системе координат.

,

2) Полярная система координат в пространстве. Полярную систему координат в пространстве образуют ориентированная плоскость , называемая экваториальной вместе с введенной на ней полярной системой координат, т.е. полюсом в точке O и полярной осью Ox и ось Oz, называемая осью зенита, которая проходит через точку O и перпендикулярна экваториальной плоскости. В полярной системе координат в пространстве положение точки M может быть охарактеризовано двумя способами: с помощью цилиндрических или сферических координат.

2.1) Цилиндрические координаты – это упорядоченная тройка чисел , где и полярные координаты ортогональной проекции точки M на плоскость , а z – координата точки M на оси Oz.

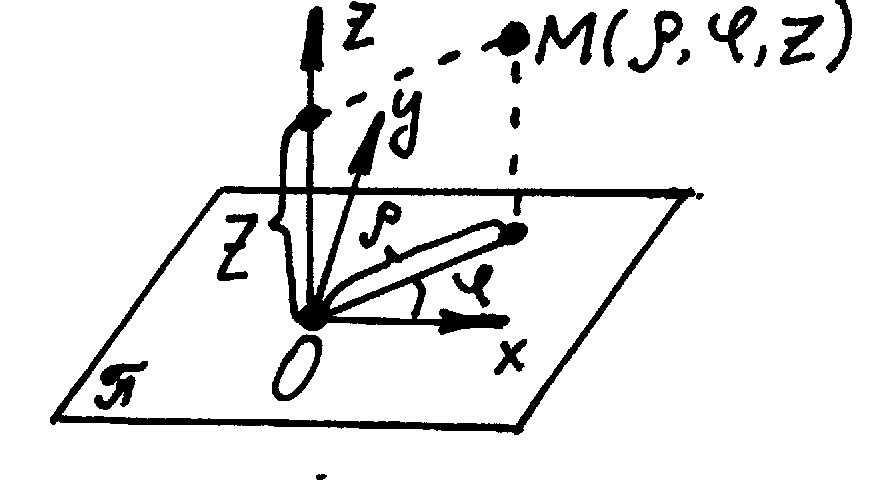
Установим связь между цилиндрическими и пространственными координатами точки M. Для этого ДПСК введем таким образом, чтобы ось абсцисс была направлена по оси Ox, а ось аппликат – по зенитной оси. Тогда

2.2.) Сферические координаты.

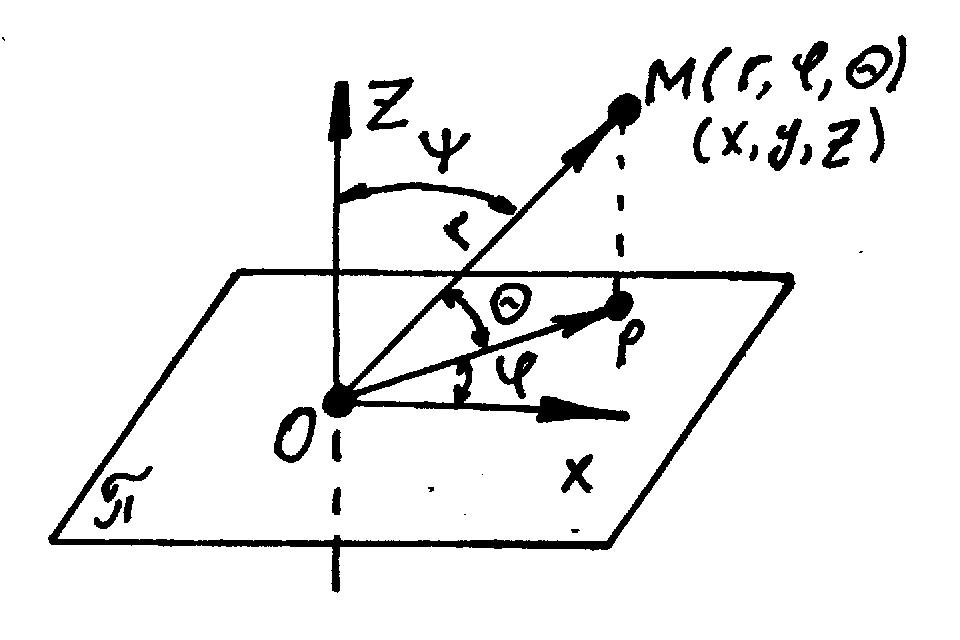
Сферическими координатами точки M называется упорядоченная тройка чисел , где r – расстояние от полюса ПСК в пространстве до точки M, т.е. длина радиус-вектора, - угол, который образует радиус-вектор к проекции, т.е. точки P, проекции точки M на экваториальную плоскость, - угол, который образует радиус-вектор с плоскостью , т.е. это угол между вектором и . Если M не лежит на экваториальной плоскости, то:

Если точка M расположена ниже экваториальной плоскости (соотносясь с направлением зенита Oz), то угол принимает отрицательные значения. Угол называется долготой точки M, a угол - широтой.

Замечание. Иногда вместо указанного угла рассматривается угол , т.е. угол, образованный радиус-вектором точки M с осью Oz. Тогда его значения изменяются от 0 до .

Установим связь между сферическими и декартовыми координатами точки M. Для этого введем в пространстве ДПСК таким образом, что длина ее масштабного отрезка совпадает с длиной масштабного отрезка ПСК, начало с полюсом, а оси абсцисс и аппликат направлены соответственно по полярной оси и оси зенита.

БИЛЕТ №23. «Эллипс»

1) Определение. Эллипсом называется геометрическое место точек на плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами и находящимися на расстоянии 2c друг от друга, есть величина постоянная 2a, где a>c>0. Для вывода уравнения эллипса введем на плоскости ДПСК таким образом, что ее ось абсцисс проходит через фокусы F₁ и F₂ в направлении от F₁ к F₂, а начало координат находится (совпадает) с серединой отрезка F₁F₂. В этой системе координат точки F₁ и F₂ имеют соответственно координаты (-с, 0) и (c, 0).

,

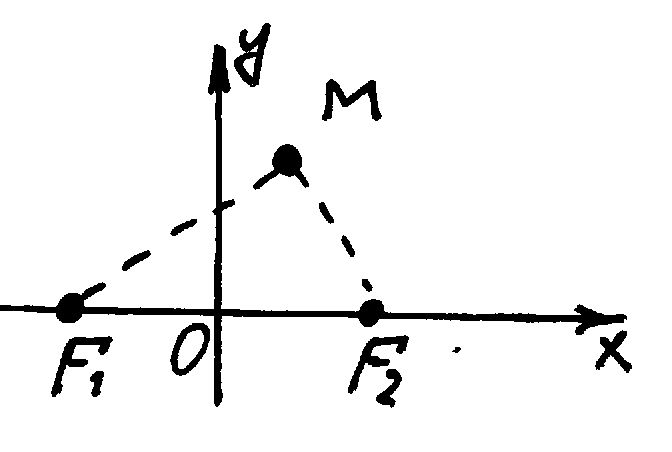
По определению справедливы соотношения (1) и (2). Т.к. если M(x, y) – точка эллипса, то:

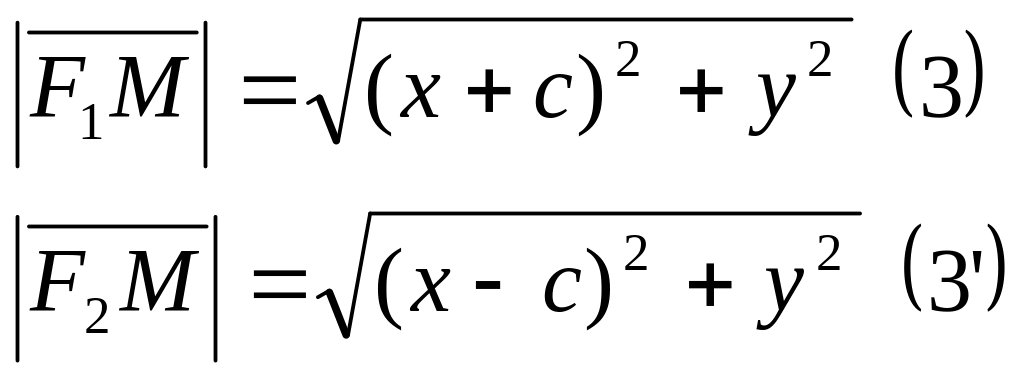
Подставим (3) и (3’) в (2) и получим соотношения:

Таким образом показано, что любая точка, лежащая на эллипсе, удовлетворяет (4). Для того, чтобы доказать, что (4) определяет эллипс, т.е. ему не удовлетворяют координаты ни каких других точек покажем, что для любой , удовлетворяющей (4), выполняются условия (1) и (2).

Из (4) вытекает, что:

Подставив в (7) (3) и (3’), получим:

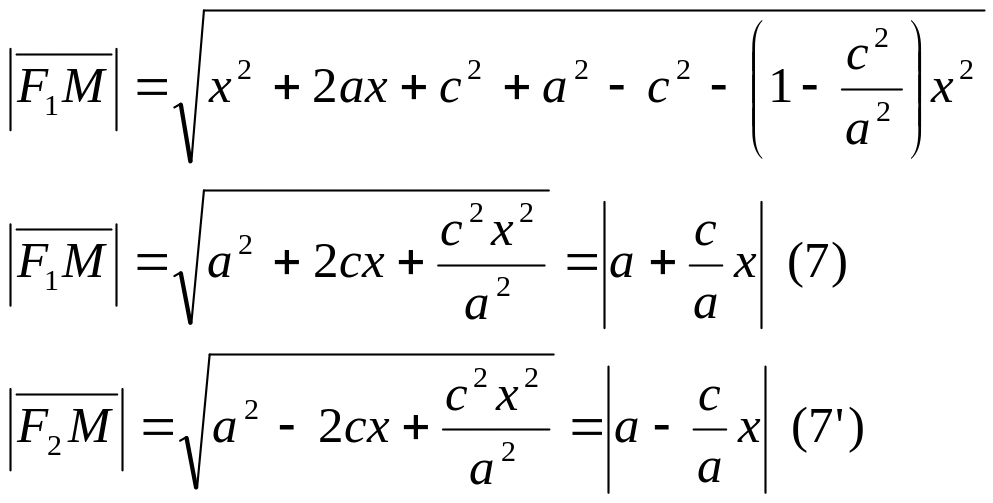
Из уравнения (4) следует, что |x| a. Тогда:

а) c<a, x>0, 0< 1, a

б) x<0, -1 ,

Таким образом доказано, что уравнение эллипса имеет вид:

2) Геометрическое изображение эллипса.

. Следовательно, эллипс, расположенный внутри прямоугольника со сторонами и . Точки, в которых эллипс пересекает оси координат, называются его вершинами. Т.к. обе переменные в уравнении входят во 2-й степени, то оси координат являются осями симметрии, а начало координат – центром симметрии.

Отрезок A₁A₂, соединяющий вершины, лежащие на той же оси, что и фокусы, называется большей осью эллипса, а перпендикулярный ему отрезок B₁B₂ – меньшей. Их половины называются большей и меньшей полуосями эллипса и имеют соответственно длина a и b. Расстояние между фокусами называется

фокальным расстоянием, а расстояние от произвольной точки эллипса до фокуса – фокальным радиусом точки M. Их длина определяется по формулам (7) и (7’). Мерой сплюснутости эллипса является его эксцентриситет , где - большая полуось, а - половина фокального расстояния. Тогда:

3) Директриса эллипса. Директрисами эллипса называются прямые, перпендикулярные большей оси. В системе координат уравнение директрисы имеет вид: , т.к. у эллипса , то для директрис, и директрисы расположены вне эллипса.

С помощью понятия директрисы эллипсу можно дать определение, эквивалентное первоначальному.

Утверждение. Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния от этой точки до фокуса к расстоянию до соответствующей директрисы (ближайшей) было равно эксцентриситету.

Из вывода уравнения эллипса следует, что фокальные радиусы точки M, т.е. расстояния от этой точки до фокуса были равны:

Для определенности рассмотрим расстояния от этой точки до и директрисы с уравнением:

Тогда:

4) Касательная к эллипсу. Для поверхности, заданной уравнением , уравнение касательной, проведенной к ней в точке , имеет вид:

(*)

Исходя из этого, составим уравнение касательной эллипса, проведенной к нему в точке :

тогда уравнение будет иметь вид:

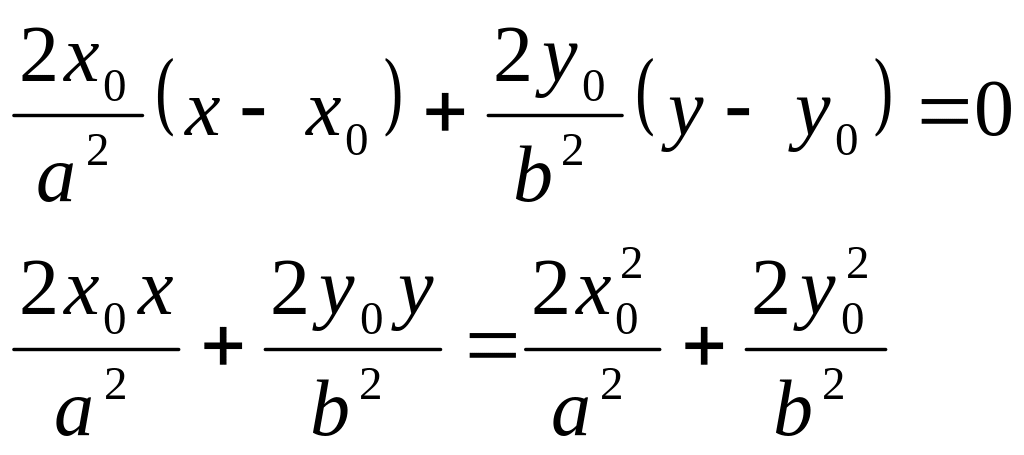
Т.к. принадлежит эллипсу, то координаты удовлетворяют равенству

Окончательно получим:

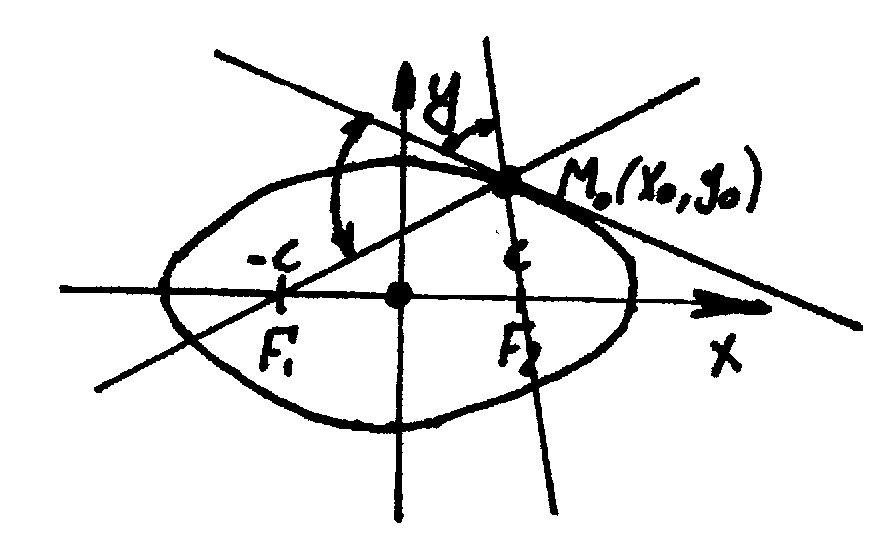
5) Оптическое свойство эллипса. Касательная, поведенная к эллипсу в точке является биссектрисой внешнего угла где и - фокусы эллипса.

БИЛЕТ №24. «Гипербола».

1) Определение. Гиперболой называется геометрическое место точек на плоскости, для которых абсолютная величина разности расстояний от этих точек до двух фиксированных, называемых фокусами, есть заданное число , причем - расстояние между фокусами.

Для вывода уравнения гиперболы введем на плоскости ДПСК, у которой ось абсцисс проходит через фокусы по направлению от к , а начало координат совпадает с серединой отрезка, соединяющего фокусы. В этой системы координат фокусы имеют координаты и

Если точка лежит на гиперболе, то выполняется соотношение:

Если точка имеет координаты , то мы имеем:

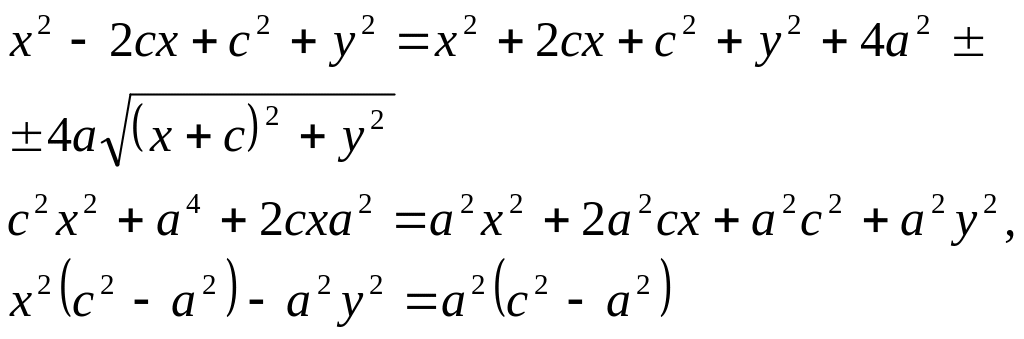Т.к. по условию , то

Таким образом показано, что любая точка, лежащая на гиперболе, удовлетворяет уравнению (2). Для того, чтобы показать, что уравнение (2) определяет гиперболу покажем, что , удовлетворяющая уравнению (2), удовлетворяет и опр. гиперболы:

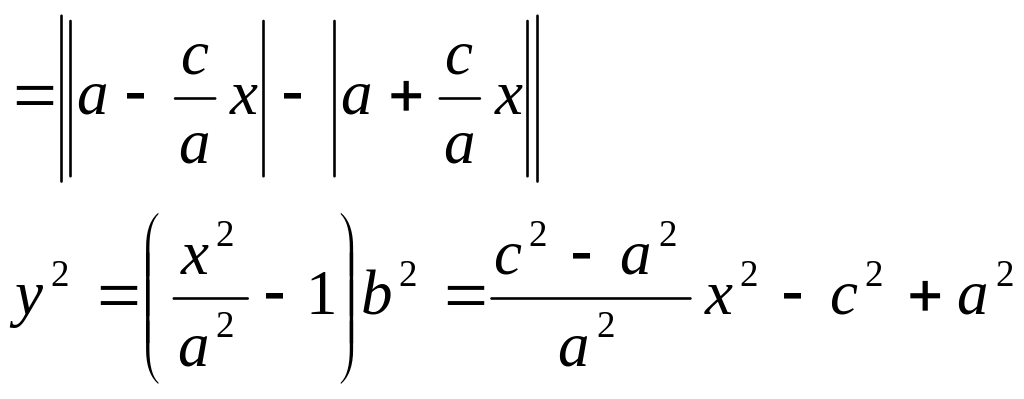
Из (2) следует, что .

,

т.е. выполняется соотношение (1). Таким образом доказывается, что уравнение гиперболы имеет вид:

2) Геометрическое изображение гиперболы. Если принадлежит гиперболе, то ей принадлежат 4 точки с любым чередованием знаков координат гипербола симметрична относительно координатных осей и начала координат, которое является ее центром симметрии.

Если гипербола задана уравнением (3), то она пересекает ось абсцисс в точках . Эти точки, т.е. точки, в которых гипербола пересекает ось симметрии, называются ее вершинами, а сама ось симметрии, пересекаемая гиперболой, называется действительной осью. В данном случае – это ось абсцисс. Покажем, что для гиперболы (3) прямая является асимптотами.

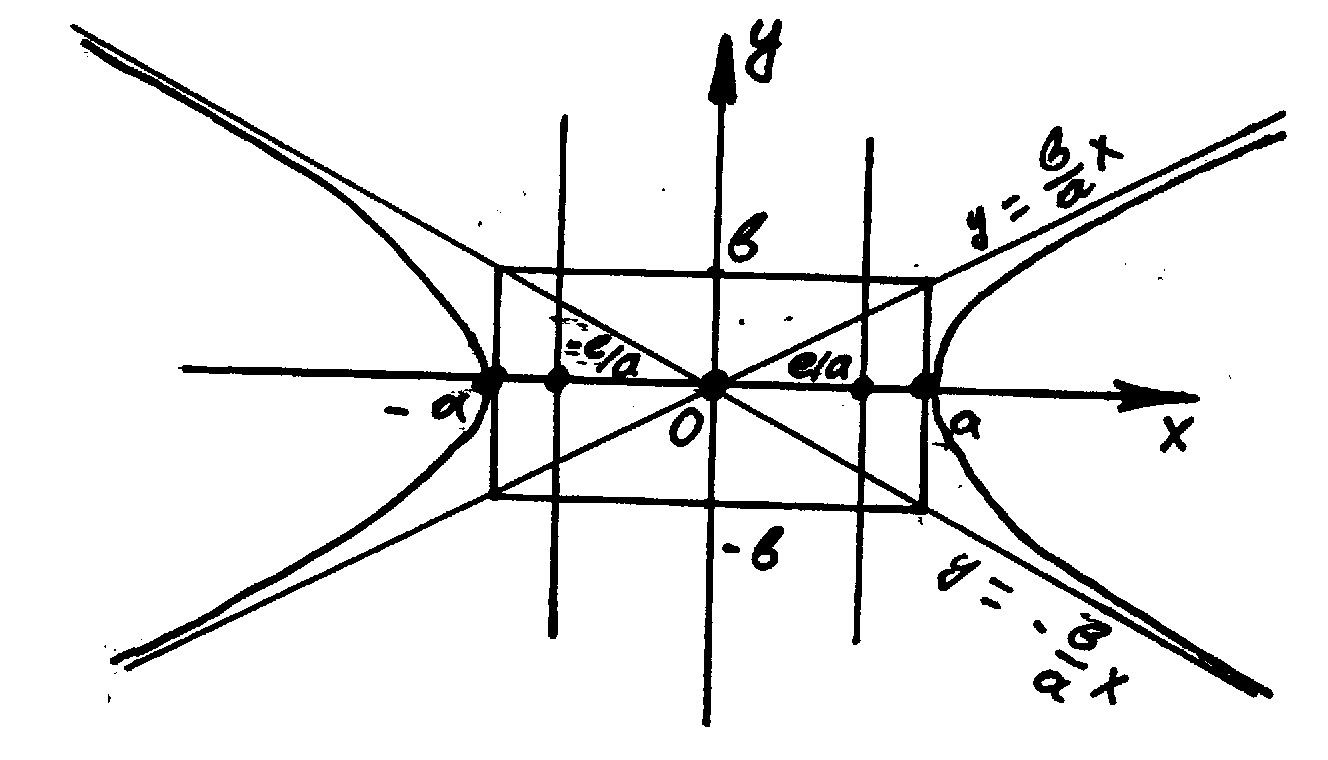
Покажем это на примере прямой . Пусть лежит на гиперболе. Найдем расстояние от точки до прямой на плоскости:

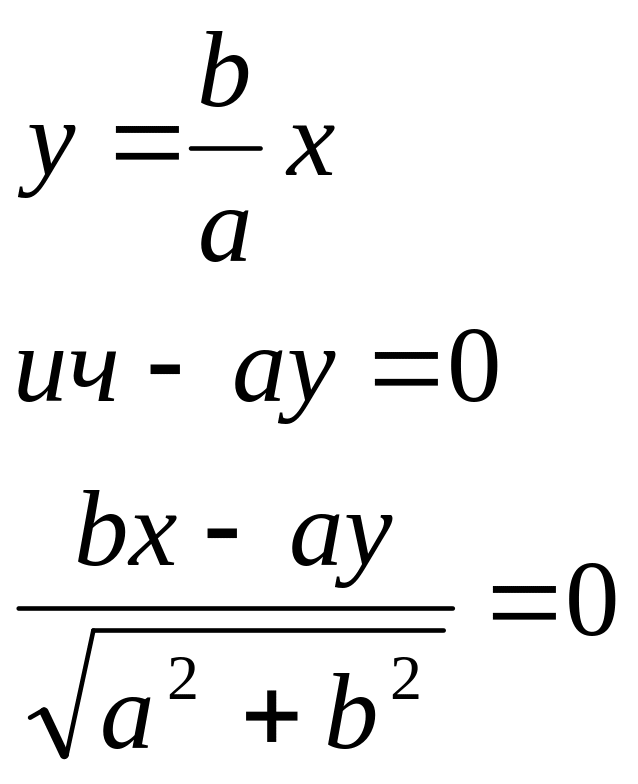
Вычислим предел d:

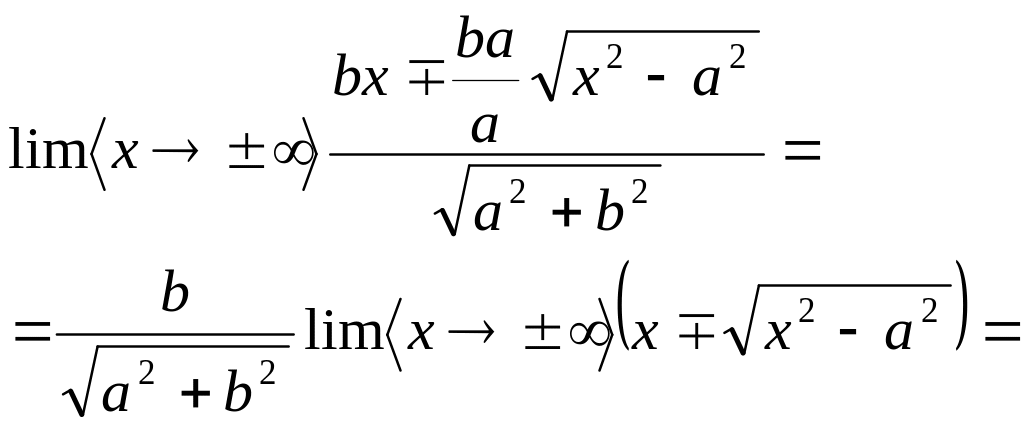
Прямая является асимптотой, также как и

Эксцентриситетом гиперболы называется отношение расстояний от центра гиперболы до фокуса к ее действительной полуоси. Используя понятие эксцентриситета, фокальные радиусы точки на гиперболе можно представить в виде:

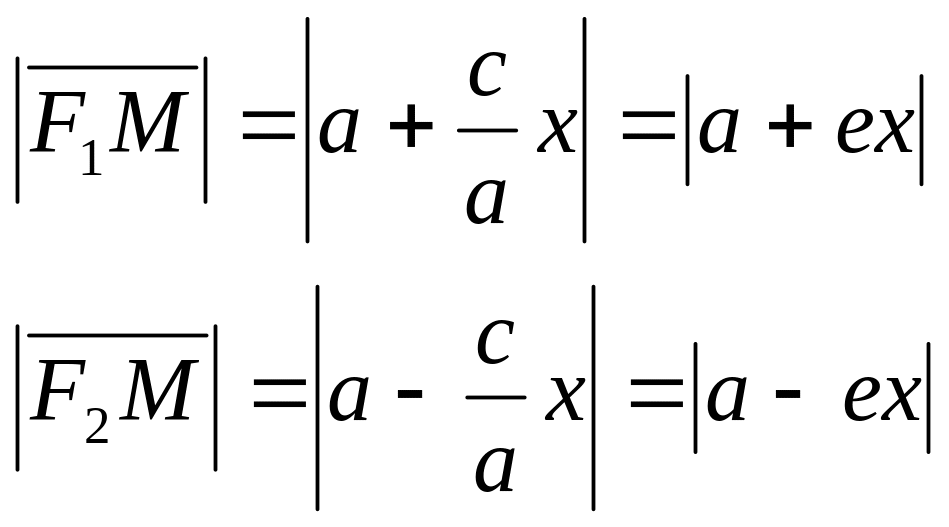
3) Директриса гиперболы. Директрисами гиперболы называются прямые, перпендикулярные ее действительной оси и отстоящие от центра гиперболы на расстояние . Таким образом, для гиперболы уравнения директрис будут иметь вид . По определению гиперболы, , , поэтому . Таким образом, директрисы пересекают прямоугольник, определяющий гиперболу.

С помощью директрисы может быть дано еще одно определение гиперболы.

Утверждение. Для того, чтобы точка лежала на гиперболе, необходимо и достаточно, чтобы отношение расстояний от этой точки до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету.

Рассмотрим для определенности точку, лежащую на правой ветви и фокус . Тогда:

4) Оптические свойства гиперболы. Касательная к гиперболе, проведенная в точке является биссектрисой внутреннего угла , где и - фокусы гиперболы.

5) Касательная к гиперболе. Пусть гипербола задана уравнением касательной к ней, проведенной в точке . Для этого уравнение гиперболы перепишем в виде и воспользуемся формулой :

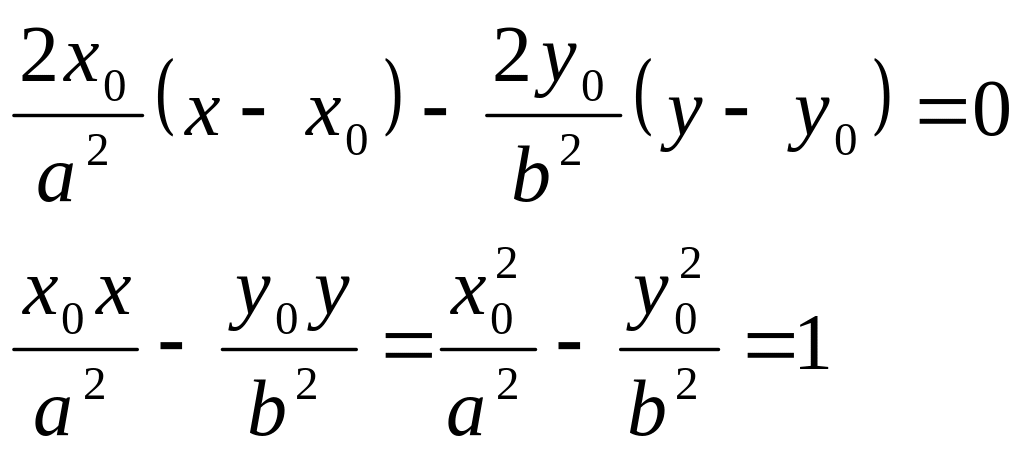
- уравнение касательной к гиперболе.

БИЛЕТ №25. «Парабола».

Параболой называется геометрическое место точек плоскости, для которых расстояния до некоторой фиксированной точки плоскости (фокус) равно расстоянию до заданной прямой (директрисы). Для того, чтобы вывести уравнение параболы, введем на плоскости ДПСК. При этом ось абсцисс проходит через фокус и перпендикулярна директрисе, причем ее направление – от директрисы к фокусу. Расстояние от фокуса до директрисы называется параметром параболы.

Если ось абсцисс пересекает директрису в точке , то расположим начало координат в середине этого отрезка. В введенной системе координат директриса имеет уравнение:

Пусть точка лежит на параболе, тогда .

(1)

Возведем обе части (1) в квадрат:

Таким образом,

(2)

Парабола имеет одну директрису. По определению параболы, расстояние от ее точки до фокуса равно расстоянию от этой точки до директрисы, поэтому эксцентриситет параболы равен 1. Из (2) следует, что если точка принадлежит параболе, то ей принадлежит и точка с координатами . В данном случае ось абсцисс (в общем случае – прямая), проходящая через фокус перпендикулярно директрисе, является осью симметрии параболы.

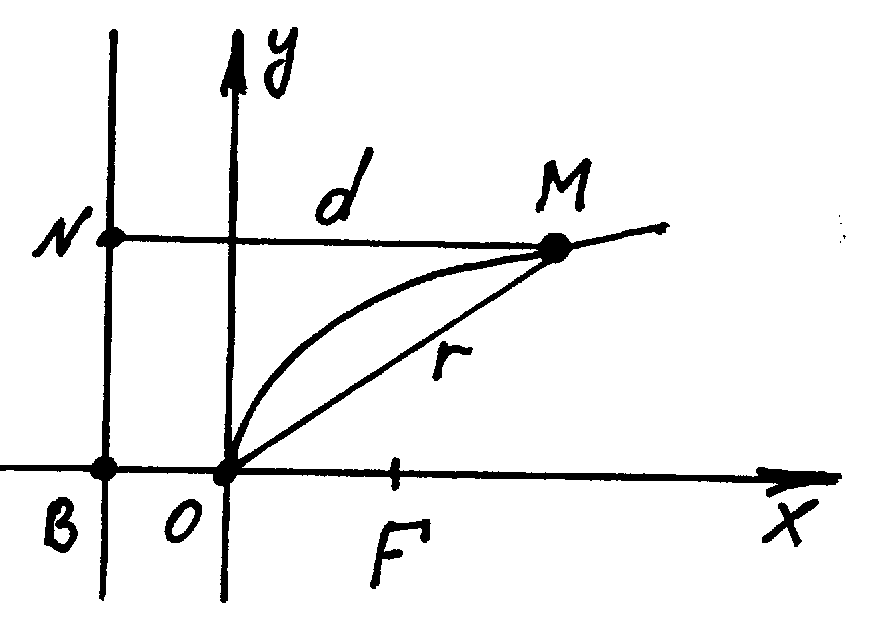
Рассмотрим касательные к параболе. Если парабола задана в виде , то получим:

Если парабола задана в виде , то мы имеем и можем воспользоваться преобразованным уравнением касательной:

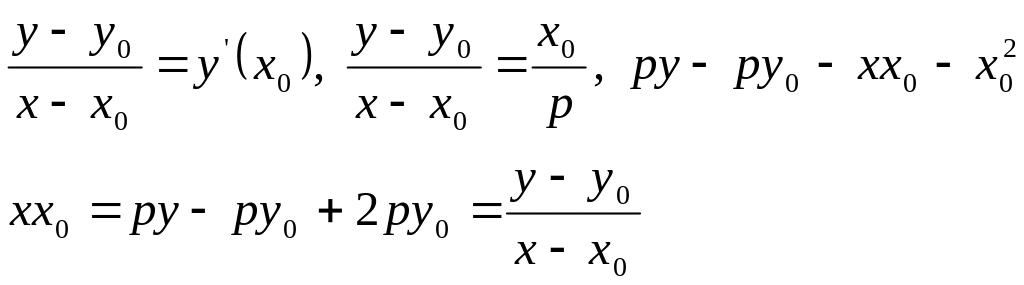
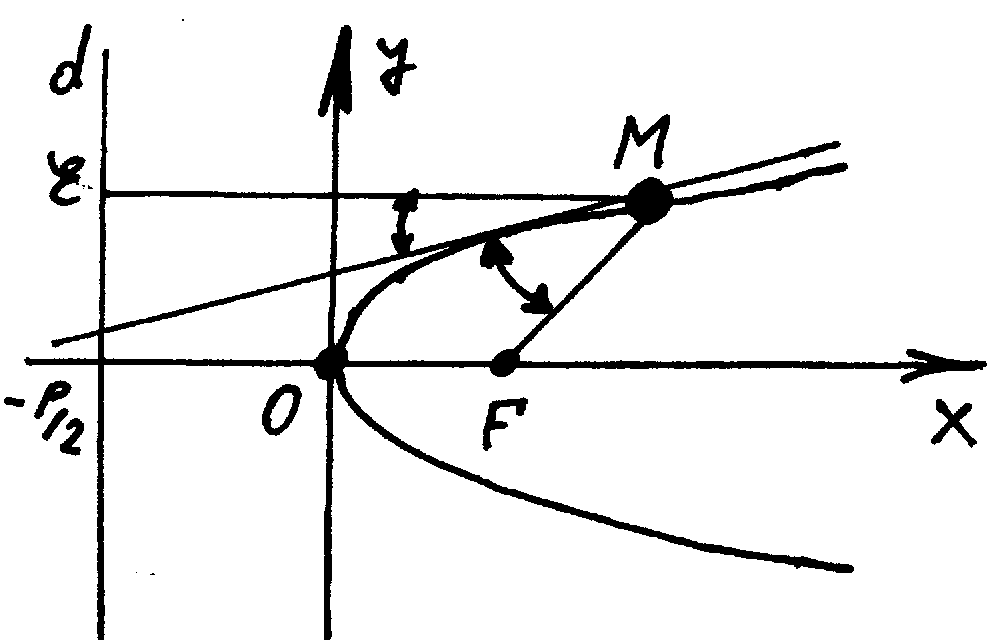
Оптические свойства.

Касательная к параболе, проведенная в точке , является биссектрисой угла , где - фокус параболы, - основание перпендикуляра, опущенного из точки на директрису.

БИЛЕТ №26. «Полярное уравнение кривой второго порядка».

Фокусной осью кривой второго порядка называется ее фокус и директриса (для гиперболы – это директриса, соответствующая данному фокусу). Пусть - основание перпендикуляра, опущенного из фокуса на директрису. Введем на плоскости полярную систему координат таким образом, что полярная ось направлена по фокальной оси в направлении от точки (директрисы) к фокусу, а полюс совпадает с фокусом.

Пусть точка - произвольная точка на кривой. Установим связь между ее радиусом и полярным углом . Опустим из перпендикуляр на директрису, - основание данного перпендикуляра. По определению эксцентриситета:

Через точку проведем фокальную хорду, т.е. отрезок прямой, перпендикулярный фокальной оси и заключенный внутри кривой. Очевидно, что точкой фокальная хорда делится пополам и половина длины фокальной хорды называется параметром кривой второго порядка. Если точка - один из концов фокальной хорды, то . Из точки также опустим перпендикуляр на директрису. Т.к. точка лежит на кривой, то через нее эксцентриситет может быть определен как:

Проведем перпендикулярно :

Подставив (3) в (1) и выполнив преобразования, получим полярное уравнение кривой:

- уравнение любой кривой второго порядка.