Билет №10. «Прямая в пространстве»

Прямая как линия пересечения двух плоскостей.

Любая прямая может рассматриваться указанным обра­зом. Координаты точек, лежащих на прямой, должны удовлетворять уравнению каждой из плоскостей. По­этому они удовлетворяют системе

(1)

Её уравнения задают в ОДСК плоскости, определяющие прямую.

Каноническое (то есть простое) уравнение прямой в ОДСК.

Если прямая в пространстве проходит через точку параллельно направляющему вектору прямой , то точка лежит на прямой в том и только том случае, когда

.

Учитывая условие компланарности векторов в ОДСК, получим уравнение, которому удовлетворяют коорди­наты точки:

(2)

Если система (1), определяю­щая прямую как линию пересечения плоско­стей, задано в ДПСК, то коэффициенты определяют нормаль к плоскостям. Поэтому в каноническом уравне­нии в качестве направляющего вектора можно рассмат­ривать векторное произведение нормали плоскости .

Уравнение прямой в ОДСК, проходящей через две точки.

Если прямая проходит через точки , то в качестве направляю­щего вектора можно взять вектор . Тогда уравнение плос­кости примет вид:

Параметрические уравнения прямой.

Если все отношения в каноническом уравнении прямой принять к значению параметра t, то получим параметри­ческое задание прямой.

(3)

Таким образом, при параметрическом задании (3) коэф­фициенты при параметрах l, m, n являются координа­тами направляющего вектора прямой. Свободные члены - координаты точки, через которую проходит прямая. Они соответствуют значениям параметра t, рав­ного нулю.

БИЛЕТ №11. «Взаимное расположение прямых в пространстве, угол между прямыми»

Взаимное расположение прямых.

Если две прямые заданы в ОДСК своими каноническими уравнениями:

то они параллельны тогда и только тогда, когда их направ­ляющие векторы

Углом между прямыми в пространстве называется угол между прямыми, проходящими через некоторую точку пространства, параллельно данной прямой. Если две прямые заданы своими каноническими уравнения в ДПСК, то косинус угла может быть определён с помо­щью скалярного произведения:

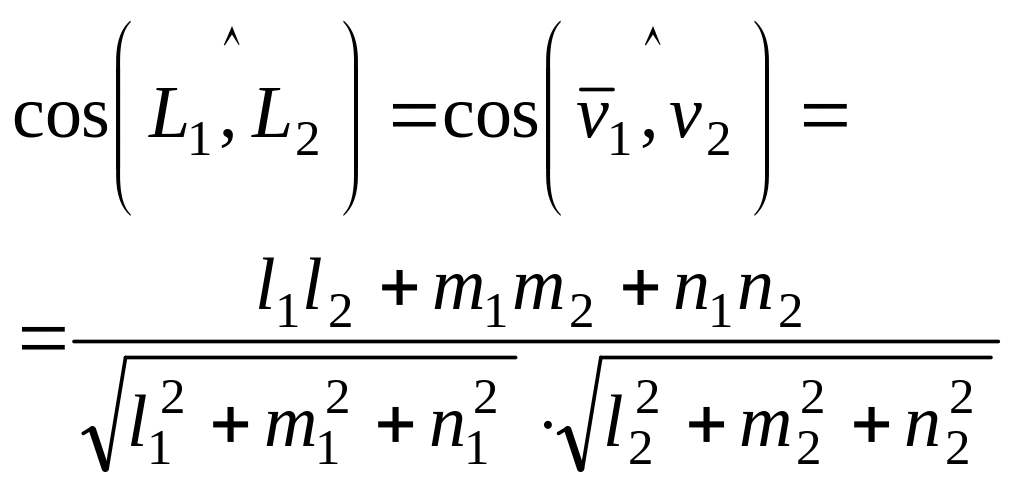(4)

Угол между прямой и плоскостью.

Пусть прямая задана каноническим уравнением, а плос­кость – общим уравнением в ДПСК:

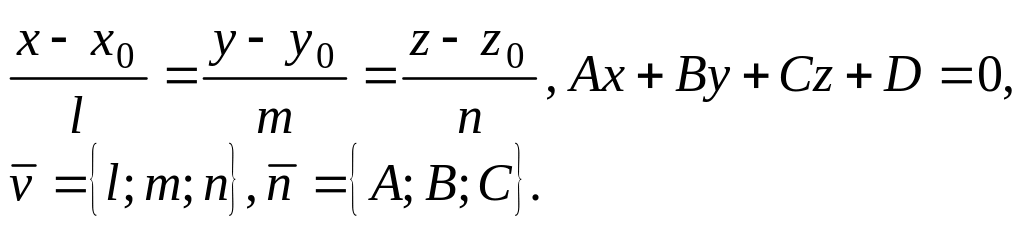
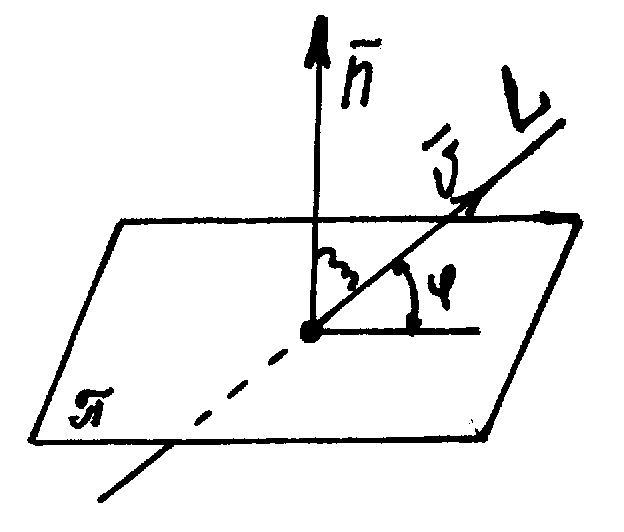
Так как угол между прямой и плоскостью – это угол ме­жду прямой и её ортогональной проекцией на плоскость, то

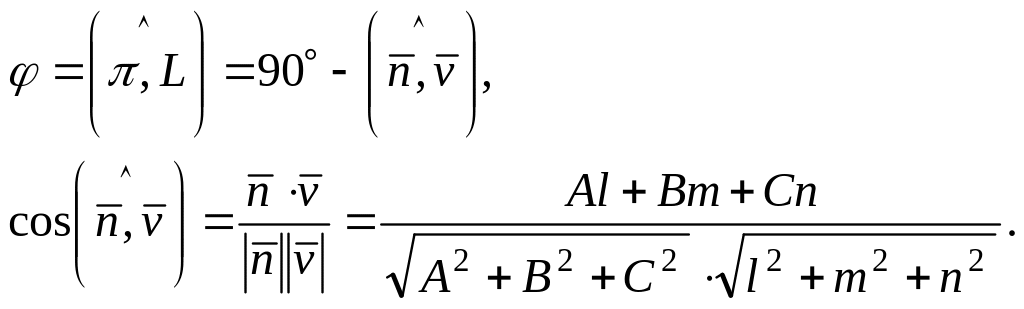
БИЛЕТ №12. «Прямая и плоскость в пространстве»

Пусть две прямые в пространстве заданы своими кано­ническими уравнениями:

L₁:

L₂:

а) Эти прямые будут скрещивающимися, то есть не пере­секаться, тогда и только тогда, когда они не могут быть расположены в одной плоскости, а, следовательно, век­торы не компланарны.

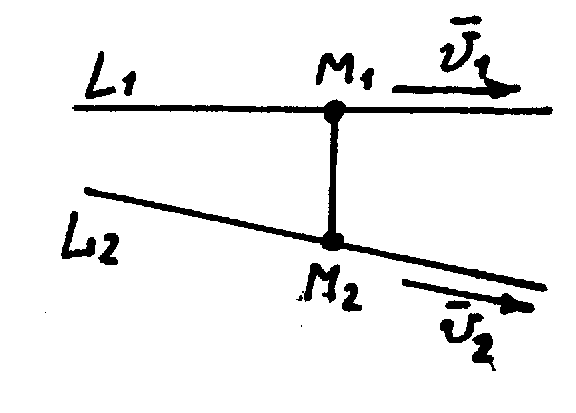
б) Прямые пересекаются.

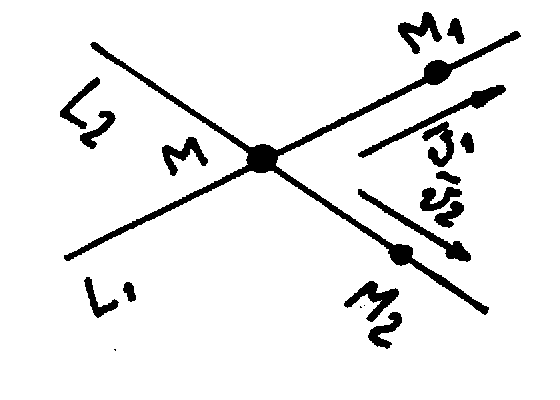
В этом случае через прямые может быть прове­дена плоскость, и определитель (2) равен нулю.

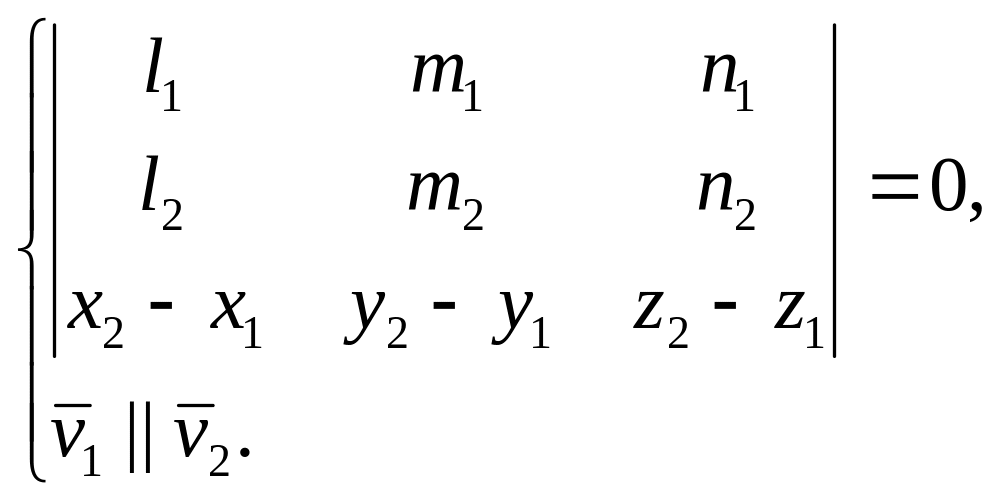(2)

в) Прямые параллельны.

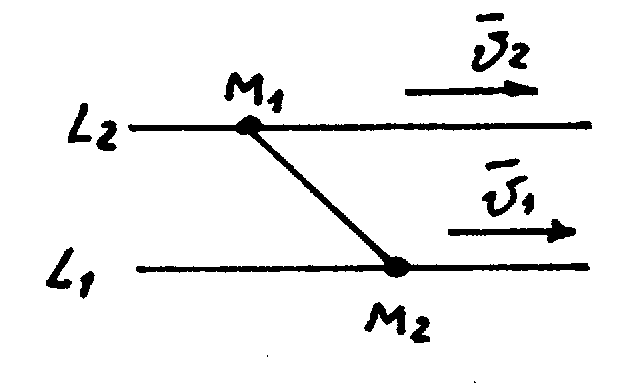
В этом случае векторы

г) Прямые совпадают.

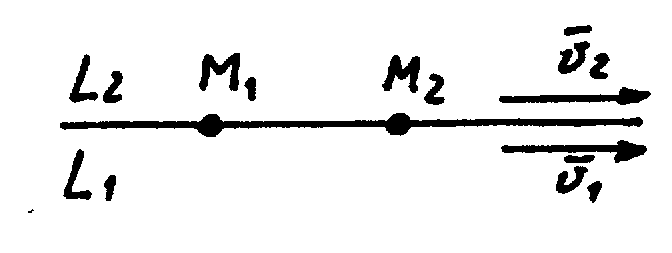
В этом случае

Взаимное расположение прямой и плоскости.

Пусть прямая задана в ОДСК каноническим уравнением а плоскость – общим уравне­нием .

а) Прямая и плоскость пересекаются.

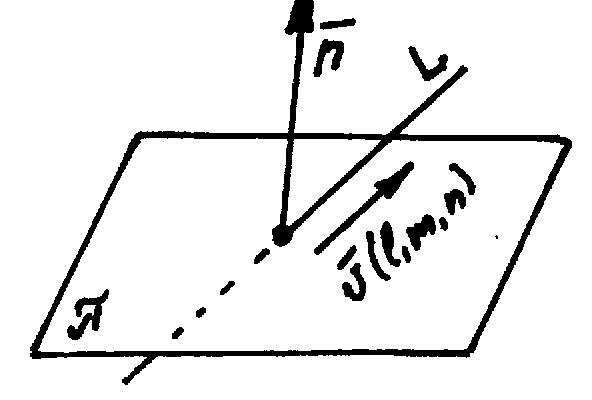
В этом случае направляющий прямой L и нормали n не перпендикулярны.

б) Прямая и плоскость параллельны..

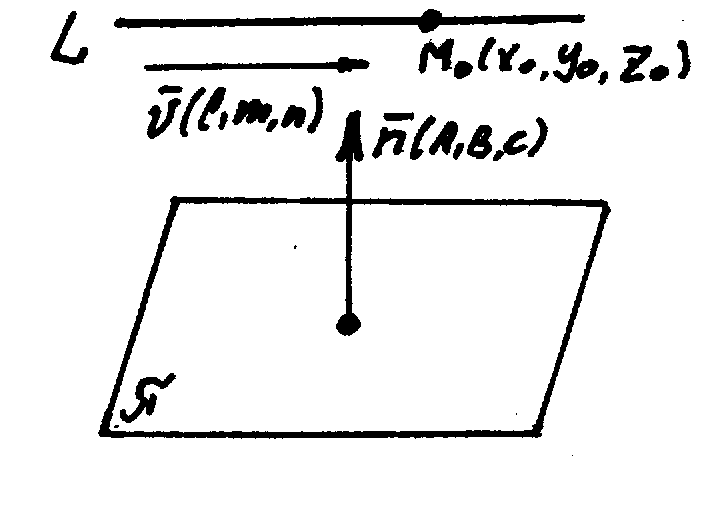
в) Прямая L принадлежит рассматриваемой плоскости.

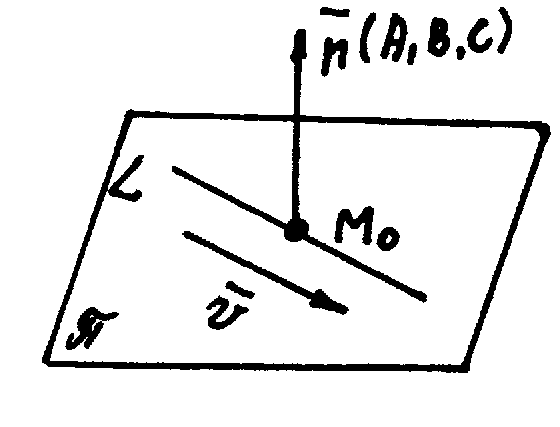
БИЛЕТ №13. «Пря­мая на плоскости»

Так как прямая на плоскости – частный случай прямой в пространстве, то она может быть определена следую­щим образом.

а)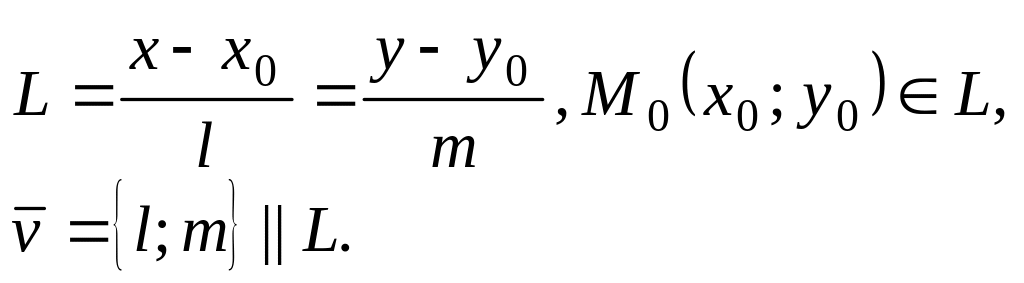

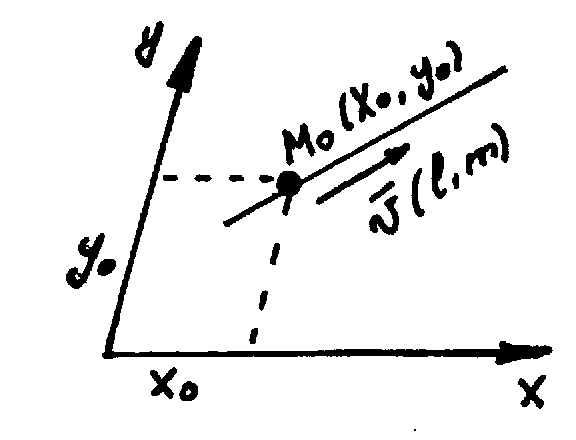
Уравнение прямой, проходящей через точки.

Так как любая прямая на плоскости XOY может рассмат­риваться как линия пересечения некоторой плоскости с плоскостью z=0, то её уравнение как линия пересечения этих плоскостей имеет вид:

(6)

Первое уравнение системы определяет плоскость , а второе – плоскость XOY.

в) Так как уравнение (6) получено из уравнения плоско­сти, в котором коэффициенты A, B, C – координаты нормали в ДПСК, то коэффициенты А, В являются коор­динатами нормали к прямой. Уравнение (6) называется общим уравнением прямой на плоскости.

Уравнение прямой на плоскости в ДПСК, проходящей через точку перпендикулярно вектору нор­мали имеет вид: .

Нормальное уравнение прямой на плоскости.

Аналогично случаю плоскости, в ДПСК нормальное уравнение прямой на плоскости имеет вид (7) , где - направляю­щие косинусы нормали к прямой, то есть координаты её орта, р – расстояние от начала координат до прямой. От общего уравнения прямой на плоскости (6) к нормаль­ному (7) можно перейти, умножив общее уравнение на нормирующий множитель:

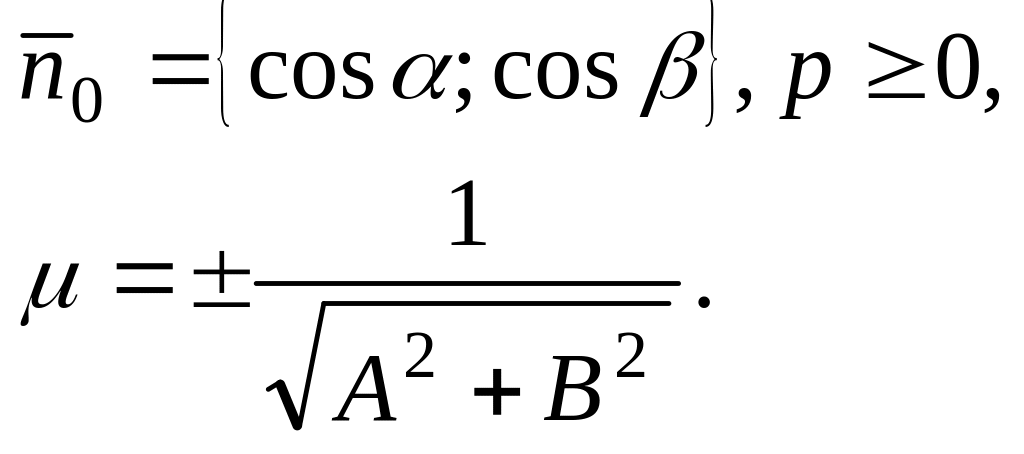
Расстояние от точки до прямой.

Если в ДПСК прямая задана нормальным уравнением, то смещением точки от этой прямой определя­ется формулой . Причём, если смещение положительно, то означает, что начало коор­динат и точка лежит на плоскости по разные сто­роны от прямой, а если смещение отрицательно, то по одну сторону. Таким образом, .

Уравнение прямой на плоскости в ДПСК с угловым коэффициентом.

Пусть прямая в ДПСК задана общим уравнением , Тогда , или k – угловой коэффициент. Выясним его смысл.

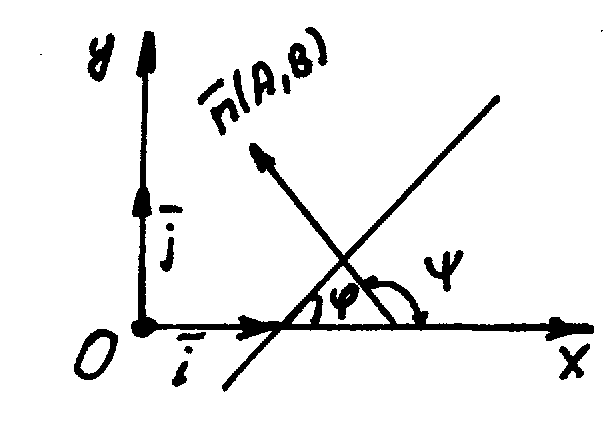
 - внешний угол.

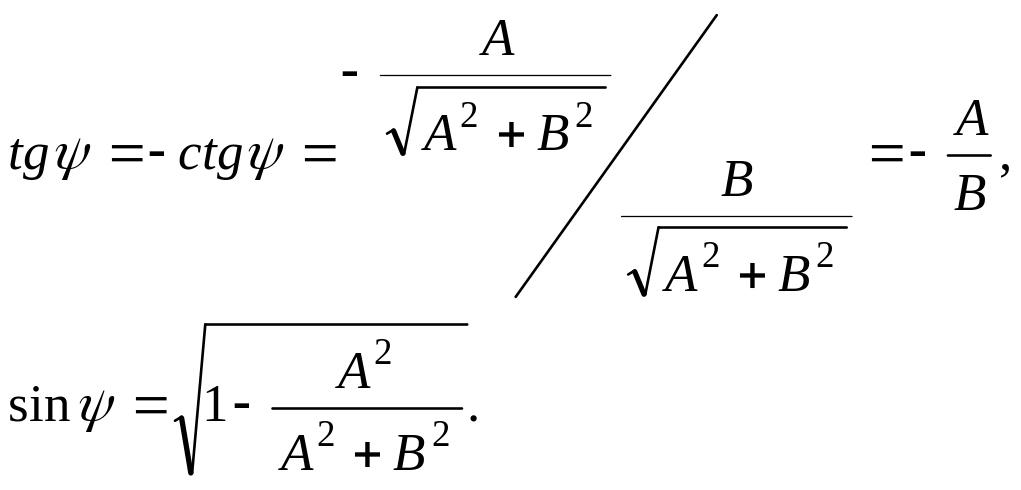
Взаимное расположение прямых на плоскости.

а) Если две прямые, заданные в ОДСК своими канониче­скими уравнениями или общими уравнениями

,

то они парал­лельны тогда и только тогда, когда

.

б) Если две прямые заданы в ДПСК, то может быть оп­ределён косинус угла между ними с помощью скаляр­ного произведения

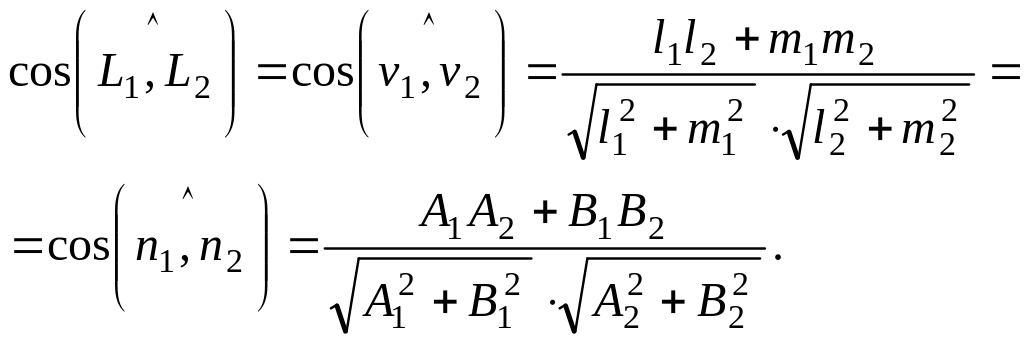
в) Если прямые заданы уравнениями с угловыми коэффициен­тами

то

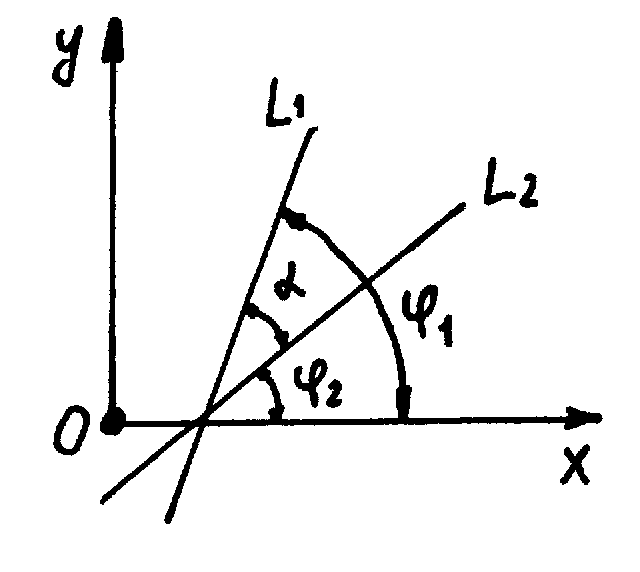
Параметрические уравнения прямой на плоскости:

.