Билет №5. «Скалярное произведение векторов, произведение векторов и его применение»

Скалярным произведением векторов и называется число, равное .

Для любых трёх векторов и любого действитель­ного числа  скалярное произведение будет обладать следующими свойствами:

1. коммутативность ;

2. ассоциативность ;

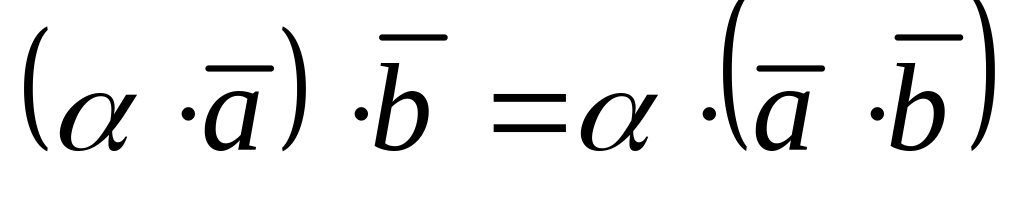3. дистрибутивность , .

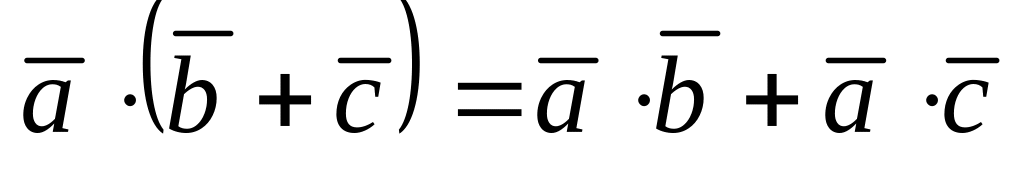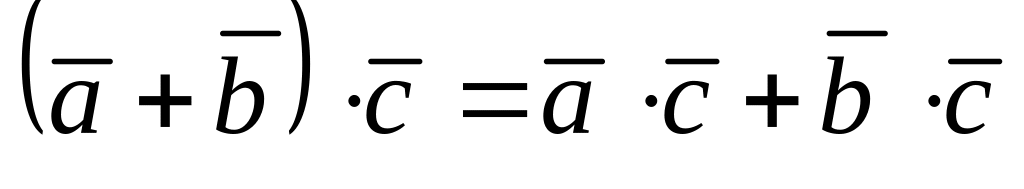Геометрический смысл скалярного произведения:

1. два ненулевых вектора ортогональны тогда и только тогда, когда ;

2. ;

3. .

Координатная форма скалярного произведения.

Пусть в пространстве зафиксирована ОДСК с масштаб­ными векторами . Векторы имеют соответст­венно координаты

и . Найдём скалярное про­изведение этих векторов.

Таким образом, скалярное произведение векторов можно вы­числить, зная таблицу умножения векторов базиса.

Если рассматривается ДПСК, то её масштабные векторы имеют единичную длину и взаимно перпендику­лярны.

.

Произведение векторов.

1. Модуль смешанного произведения равен объ­ёму параллелепипеда, построенного на векторах каждой строки.

2. Объём тетраэдра равен .

.

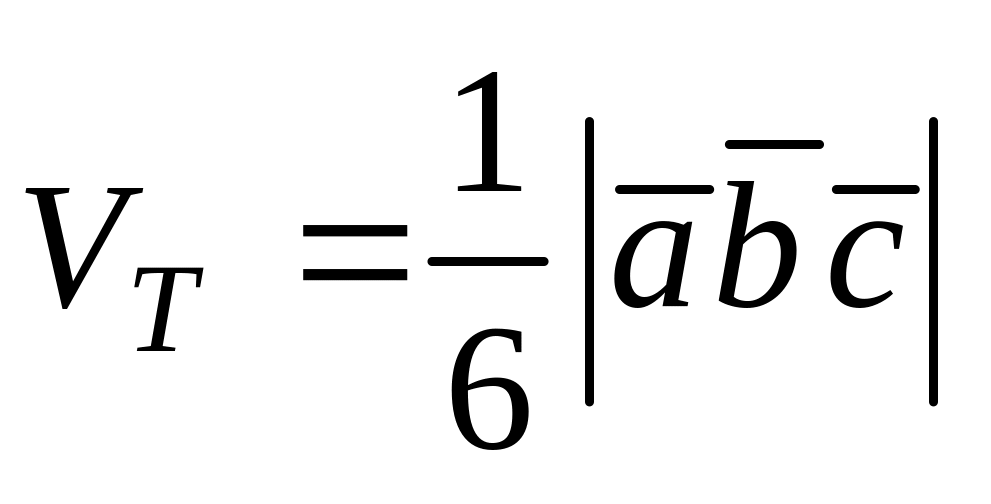3. Если смешанное произведение больше нуля, то тройка векторов - правая, если меньше, то – левая.

4. Если смешанное произведение , то век­торы - компланарны.

Координатная форма произведения векторов

Если векторы заданы своими координатами в ДПСК то

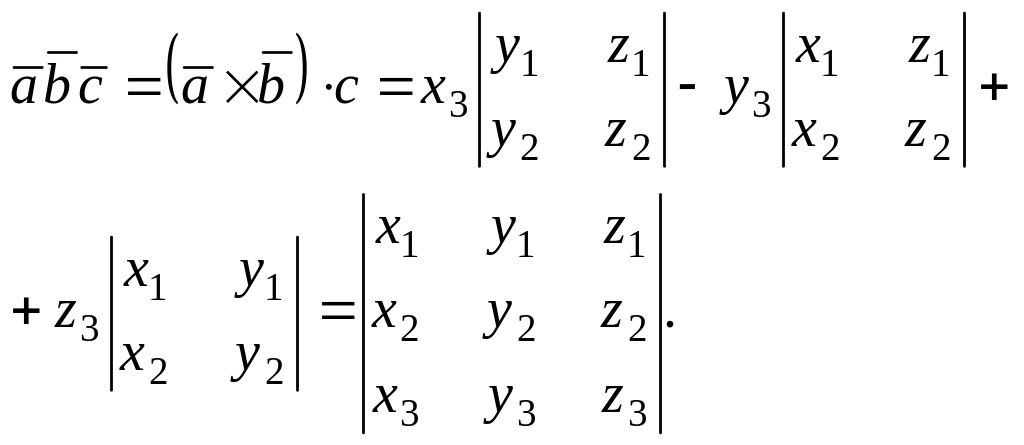
Условие коллинеарности векторов.

Если векторы заданы своими координатами в ДПСК, то с одной стороны их векторное произведе­ние равно нулю, а с другой –

откуда следует усло­вие коллинеарности векторов

Применение произведения векторов.

Направляющие косинуса вектора – это косинусы уг­лов, которые вектор образует с осями координат.

Ортом вектора называется вектор, коллинеарный и сонаправленный с исходным, но имеющий единич­ную длину. Аналогично определяется орт оси. Оче­видно, если задан вектор , то его орт будет равен . Действительно, определённый так вектор коллинеарен и сонаправлен с вектором и его длина

.

Очевидно, что если , то его орт будет иметь координаты

Сравнивая с выражениями для направляющих коси­нусов, получим, что координатами орта вектора в ДПСК в точности являются направляющие коси­нусы данного вектора.

БИЛЕТ №6. «Векторное произведение векторов».

Векторным произведением векторов и называется вектор , у которого , а направление определяется следующим способом:

1) , то есть в случае ненулевых сомножите­лей вектор перпендикулярен к плоскости, которую они определяют.

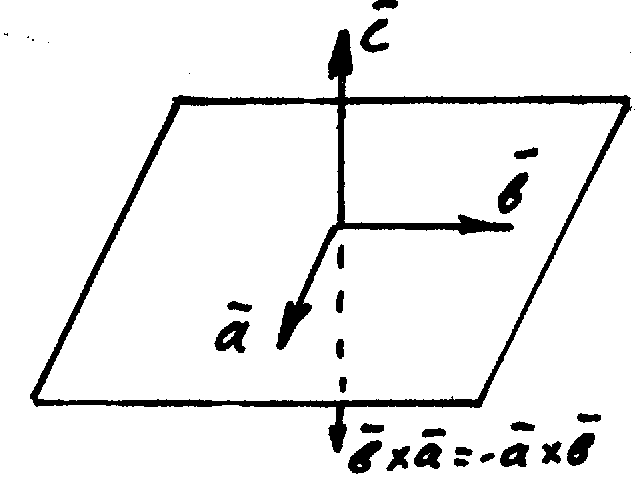
2) если тройка векторов является правой, то век­тор направлен вверх.

Для любых трёх векторов и любого действитель­ного числа  векторное произведение будет обладать следующими свойствами:

1. антикоммутативность: ;

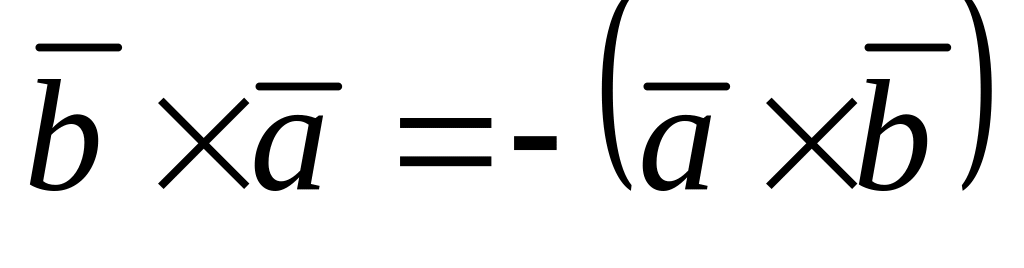2. ассоциативность относительно умножения на число: ;

3. дистрибутивность:

Геометрический смысл векторного произведения.

Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулю.

Площадь параллелограмма, построенного на векто­рах и , равна модулю векторного произведения

.

Площадь треугольника, построенного на векторах равна половине модуля векторного произведе­ния

Координатная форма векторного произведения.

Пусть в ОДСК векторы имеют соответственно координаты и . Если - масштабные векторы данной системы, то

(*)

Таким образом, как и в случае скалярного произве­дения, векторное произведение двух векторов при фиксированном базисе полностью определяется таблицей векторного умножения векторов базиса. Составим такую таблицу для ДПСК.

X
	0
		0
			0

Таблица умножения: элемент строки умножают на элемент столбца.

Исходя из данной таблицы, подставим вместо в формулу (*). Получим формулу вычисле­ния векторного произведения в координатной форме в ДПСК:

Для более лёгкого запоминания формулы (**) ис­пользуется символическая запись

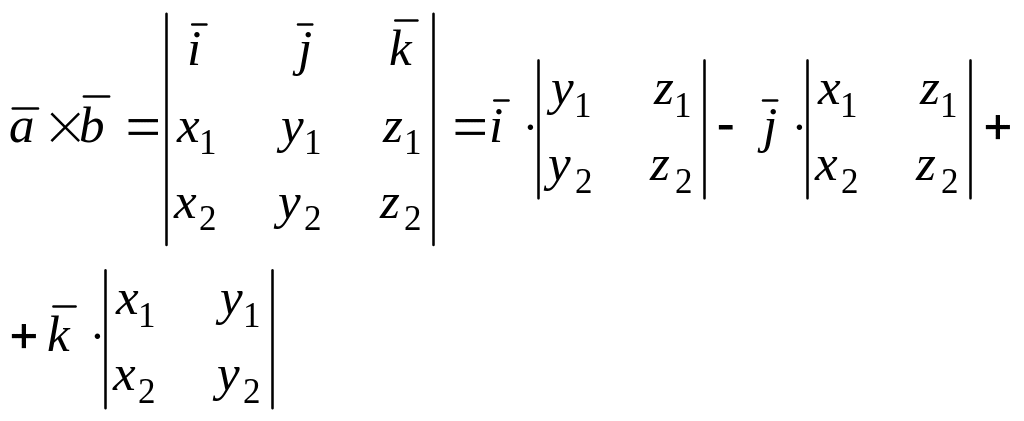
БИЛЕТ №7. «Смешанное произведение векторов».

Смешанным произведением трёх векторов называется число , равное скалярному произведению первых двух сомножителей и третьего сомножителя .

Для любых трёх векторов и любого действи­тельного числа  смешанное произведение векторов будет обладать следующими свойствами:

1. ассоциативность:

;

2) дистрибутивность:

;

3) результат смешанного произведения не меняется при циклической перестановке сомножителей .

Геометрический смысл смешанного произведения.

Рассмотрим случай, когда тройка векторов - правая, то есть вектор направлен в то полупро­странство, на которое пространство разбивает плос­кость, определяемую векторами , в которое на­правлен правый винт, идущий от к .

На векторах построим параллелепипед. Вы­числим объём данного параллелепипеда:

(По определению, объём параллелепипеда равен про­изведению площади основания на высоту, опущен­ную на это основание.)

Вектор направлен в полупространство, противопо­ложное тому, куда направлен правый винт, идущий от к . Следовательно, .