www.ilya-corp.narod.ru представляет

Н.В. Симонян

И.В. Щербаков

С.В. Марканчев

Экзаменационные билеты по Аналитической геометрии

I семестр

Тула – 2002

Содержание

• Содержание .................................................................................................................................................. 2

• Билет №1. Аналитическая геометрия на прямой ...................................................................................... 3

• Билет №2. Параллельное проектирование, деление отрезка в заданном соотношении ........................ 3

• Билет №3. Линейные операции над векторами ......................................................................................... 4

• Билет №4. Линейная зависимость и независимость векторов ................................................................. 4

• Билет №5. Скалярное произведение векторов, произведение векторов и его применение .................. 5

• Билет №6. Векторное произведение векторов ........................................................................................... 7

• Билет №7. Смешанное произведение векторов ........................................................................................ 7

• Билет №8. Плоскость в пространстве: общее уравнение, неполное уравнение,

уравнение плоскости в отрезках, уравнение плоскости, проходящей через три точки .......................... 8

• Билет №9. Плоскость в пространстве: взаимное расположение плоскостей, нормальное уравнение

плоскости, расстояние от точки до плоскости ............................................................................................. 9

• Билет №10. Прямая в пространстве ............................................................................................................ 10

• Билет №11. Взаимное расположение прямых в пространстве, угол между прямыми ........................... 11

• Билет №12. Прямая и плоскость в пространстве ....................................................................................... 11

• Билет №13. Прямая на плоскости ................................................................................................................ 12

• Билет №14. Пучок плоскостей ..................................................................................................................... 13

• Билет №15. Связка плоскостей .................................................................................................................... 14

• Билет №16. Преобразование системы координат на плоскости: перенос ОДСК и переход

от старой ОДСК к новой с тем же началом ..................................................................................................14

• Билет №17. Общее преобразование ОДСК на плоскости: связь между координатами вектора

при преобразовании системы координат на плоскости .............................................................................. 15

• Билет №18. Связь между координатами точки при переходе от одной ДПСК к другой ....................... 16

• Билет №19. Преобразование координат в пространстве: переход в пространстве от старой

системы координат к новой с тем же началом, общее преобразование ОДСК ........................................ 16

• Билет №20. Преобразование ДПСК в пространстве .................................................................................. 17

• Билет №21. Углы Эйлера .............................................................................................................................. 18

• Билет №22. Полярные системы координат ................................................................................................. 18

• Билет №23. Эллипс ........................................................................................................................................ 20

• Билет №24. Гипербола ................................................................................................................................... 21

• Билет №25. Парабола .................................................................................................................................... 23

• Билет №26. Полярное уравнение кривой второго порядка ....................................................................... 24

© 2002. Все права защищены.

Симонян Н.В., Щербаков И.В., Марканчев С.В.

Гарнитура Таймс, бумага для принтеров A4.

Билет №1. «Аналитическая геометрия на прямой»

Направленным отрезком называется упорядоченная пара точек А и В, одна из которых (точка А) называется началом, а вторая (точка В) – концом.

Осью называется прямая, на которой задано положи­тельной направление и указан масштабный отрезок.

Координатой направленного отрезка, лежащего на оси, называется число, равное длине данного отрезка в за­данном масштабе. В случае, когда направление отрезка совпадает с положительным направлением оси и число, противоположное длине, если направленный отрезок имеет направление, противоположное положительному направлению.

Осью координат называется ось, на которой указана точка О – точка начала координат. Координаты точки М, лежащие на оси координат, называются координаты на­правленного отрезка .

Теорема 1.1. Если точки А,, В, и С лежат на оси, то координата направленного отрезка равна сумме направленный отрезков и в независимости от расположения точки.

Теорема 1.2. Если направленный отрезок, лежащий на оси координат, задан своим началом и концом точками , то координата направленного отрезка равна .

Следствие. Существует связь между координатами точки М, лежащей на оси в различных системах коор­динат.

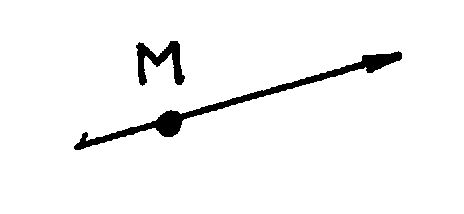
Пусть оси координат имеют одинаковые масштабные отрезки и положительные направления, а отличаются лишь своими началами: первое из них (старое) имеет своим началом точку О, а второе (новое) – точку О. Если точка М имеет на старой оси координат имеет ко­ординату х, а на новой - х, то связь между ними имеет вид , где - координата начала новой оси координат на старой.

Направленные отрезки называются коллинеарными, если они расположены на параллельных (или совпадающих) прямых. (Направленные отрезки предполагаются невы­рожденными, то есть их конец не совпадает с началом.)

Если коллинеарные отрезки имеют одинаковое направ­ление, то они называются сонаправленными ; если разное направление, то противопо­ложно направленными. Два невырожденных направлен­ных отрезка называются равными, если:

1. они коллинеарны;

2. сонаправлены;

3. имеют равные длины.

Свободным вектором называется класс всех равных ме­жду собой направленных отрезков.

Длиной вектора называется длина любого направлен­ного отрезка, входящего в обозначаемый ими класс; два вектора коллинеарны, если коллинеарны направленные отрезки, входящие в обозначаемые ими классы, и коор­дината вектора называется координатой направленного отрезка, входящего в обозначаемый ими класс.

Класс всех вырожденных направленных отрезков назы­вается нулевым вектором. Его длина равна нулю.

Система координат на плоскости и в пространстве.

Общей декартовой системой координат (ОДСК), или аффинной, на плоскости называется упорядоченная пара осей координат, пересекающихся в своих началах.

Частном случаем ОДСК является декартова прямо­угольная система координат (ДПСК), оси которой вза­имно перпендикулярны и имеют одинаковые масштаб­ные отрезки. ОДСК в пространстве называется упорядо­ченная тройка осей координат, не лежащих в одной плоскости и пересекающихся в своих началах.

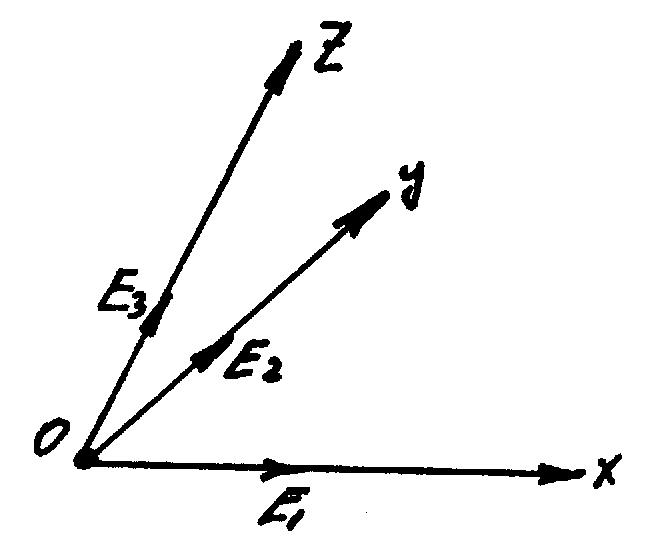
ДПСК в пространстве называется ОДСК, в которой оси взаимно перпендикулярны и имеют одинаковые мас­штабные отрезки.

Теорема 1.3. Если направленный отрезок на плоско­сти задан своими координатами начала и конца , ( , ), то его координаты имеют вид , или

- для пространственного случая.

Билет №2. «Параллельное проектирование, деление отрезка в заданном отношении»

1)

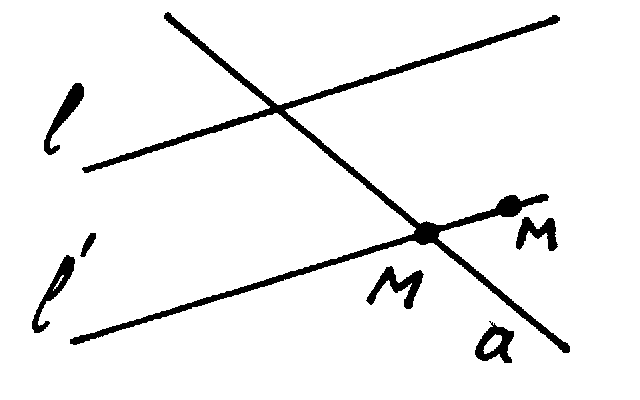
Проекцией точки М на прямую а, параллельно прямой b, называется точка М - точка пересечения прямых l и l. (В случае, когда точка М не лежит на прямой а; если точка М лежит на прямой а, то её проекция совпадает с самой точкой.)

2)

Проекцией точки М на прямую а, параллельную плоско­сти Р, называется точка пересечения данной прямой с плоскостью, проходящей через точку М, параллельно плоскости Р. (В случае, когда точка М не лежит на пря­мой а.)

3) Проекцией точки М на плоскость Р, параллельно прямой l, называется точка пересечения плоскости Р с прямой, проходящей через точку М параллельно прямой l.

Проекцией направленного отрезка при любом из видов параллельного проектирования называется направлен­ный отрезок, началом которого является проекция на­чала исходного отрезка, а концом – проекция конца.

Операция параллельного проектирования сохраняет отношения длин направленных отрезков.

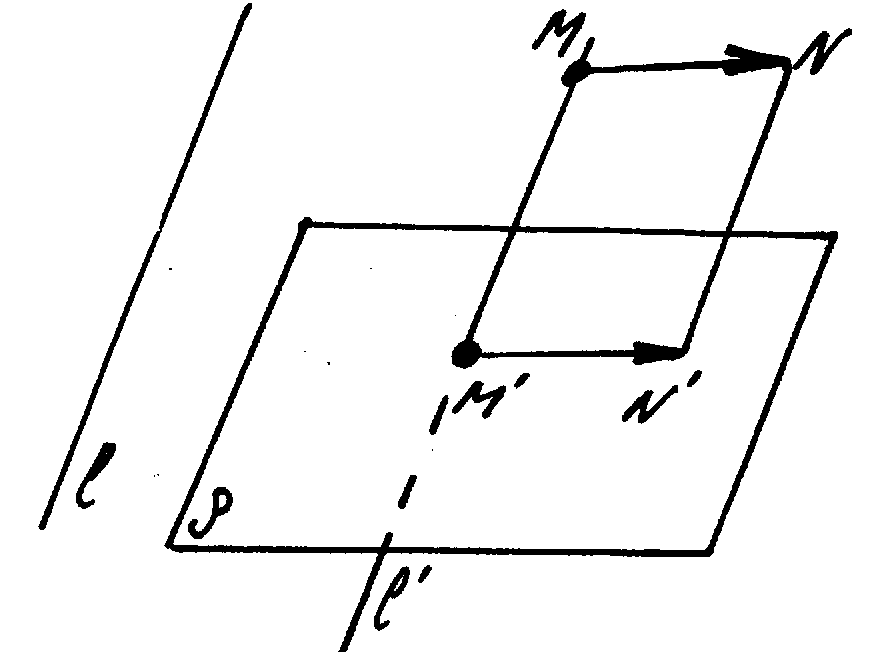
Деление отрезка в заданном отношении.

Если А и В – точки на оси в пространстве, заданные со­ответственно своими координатами и , то точка С , расположенная внутри АВ, делит его в отношении , равное тому из трёх чисел , , , знаменатель которого отличен от нуля, и каждому из них, если все знаменатели нену­левые.

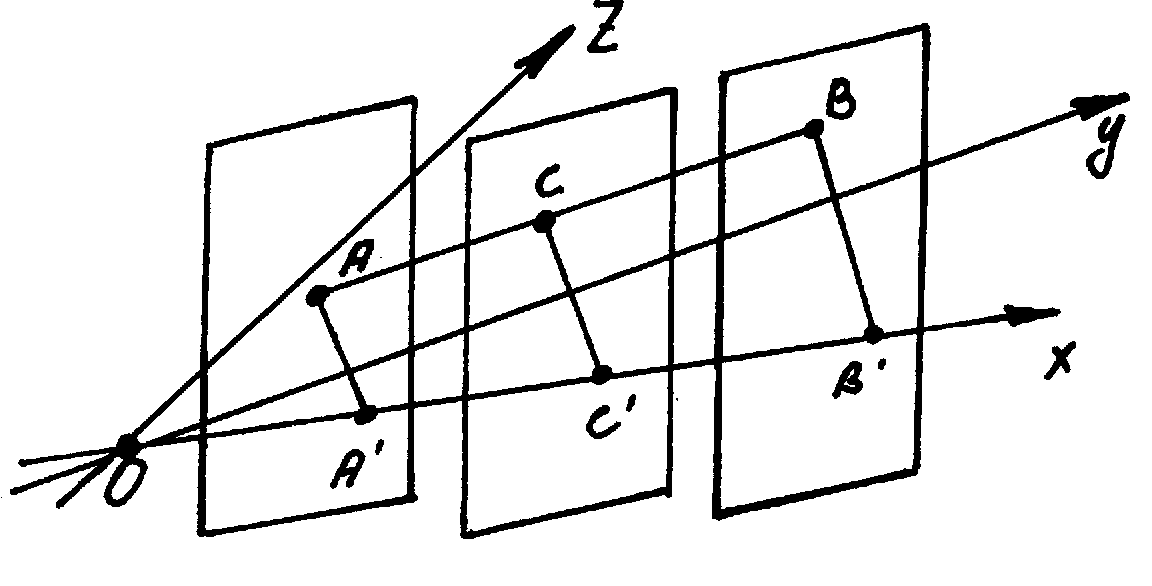
Доказательство. Введём в пространстве ОДСК, в кото­рой заданы координаты рассматриваемых точек. Спро­ектируем точки А, В, С на ось ОХ, параллельно плоско­сти YOZ.

Точки А, В, С - проекции точек А, В, С на ось ОХ. При этом точка С в случае несовпадения с точкой А делит отрезок АВ в отношении , но параллельное проектирование сохраняет отношение длин отрезков, поэтому в этом же отношении делится отрезок АВ точ­кой С. Оставшиеся отношения получаются аналогич­ными при параллельном проектирования на остальные оси.

Билет №3. «Линейные операции над векторами»

Сложение векторов.

Суммой векторов и называется вектор , началом которого называется произвольная точка пространства О, а концом – точка В, которая получается следующим образом: если от точки О отложить , а от точки А отложить .

Для любых трёх векторов операция сложения будет обладать следующими свойствами:

1. ассоциативность ,

2. коммутативность ,

3. существование нулевого вектора ,

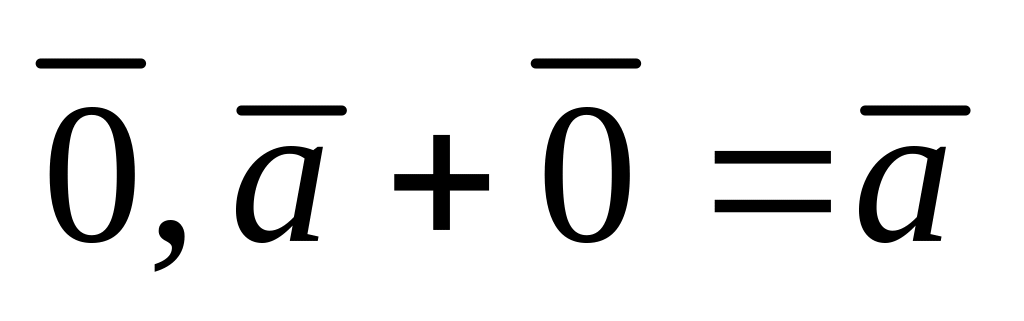4. существование противоположного вектора .

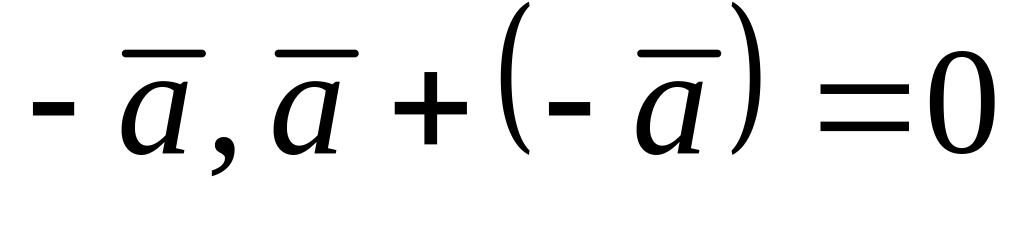Очевидно, что в качестве противоположного вектора для выступает вектор, коллинеарный , имеющий с ним одинаковую длину, но противоположно направленный.

Разностью векторов называется вектор , такой, что .

Для нахождения разности (или суммы) используют пра­вило параллелограмма или треугольника.

Умножение вектора на число.

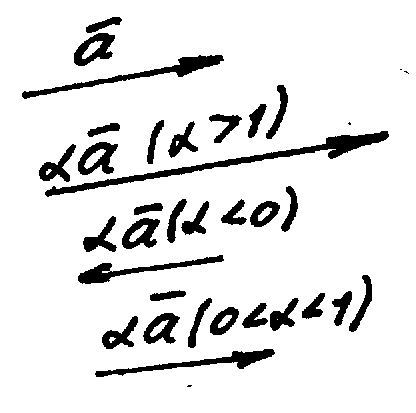
Произведением числа  на вектор называется вектор, коллинеарный исходному и сонаправленный с ним, если >0, и противоположно направленный, если <0.

Для любых двух чисел  и  и двух векторов и операция умножения вектора на число будет обладать следующими свойствами:

1) ;

2) ассоциативность умножения на число

;

3) дистрибутивность умножения на число:

,

.