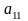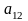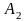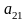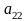- •1.Опуклі множини та їх властивості
- •2.Загальна злп та її допустима область
- •3.Графічний метод розв’язування задач лінійного програмування
- •4. Загальна економіко-математична модел задачі лінійного програмування
- •5. Алгоритм симплекс методу
- •Скiнченнiсть симплекс-методу
- •Симплекс-таблицi
- •7. Метод штучного базису
- •Зв’язок міжрозв’язками пари двоїстихзадач.Теорема двоїстості
- •12.Муравйов
- •13.Олішевський
- •14.Методи знаходження початкового базисного розвязку тзлп
- •1. Метод пiвнiчно-захiдного кута
- •2. Метод мінімального елемента
- •17.Рудик
- •18.Рудик
- •19.Аракелова
- •24. Метод відтинання. Алгоритм Гоморі
- •25. Частково цiлочисельнi задачі лінійного програмування. Другий метод Гоморi
- •26. Третiй метод Гоморi
- •Алгоритм третього методу Гоморi
- •5. Знаходимо індекс l з умови: де мінімум визначається на
- •27.Стельмах
- •28.Стельмах
- •Задачі теорії гри
- •Основні поняття теорії ігор
- •Матричні ігри двох осіб
- •Гра зі змішаними стратегіями
- •Геометрична інтерпретація гри теорії гри
- •Зведення матричної гри до задачі лінійного програмування
- •33 Теорема про активні стратегії
- •34.Загальна постановка задачі нелінійного програмування. Класифікація задач
- •35. Геометрична інтерпретація задачі нелінійного програмування
- •36.Метод множників Лагранжа
- •37.Узагальнення методу множників Лагранжа. Теорема Куна-Таккера. Теорема Куна—Таккера
- •38.Градієнтні методи безумовної оптимізації
першому випадку з подальшого розгляду виключається перший рядок
транспортної таблиці, покладаємо b1 = b1 – x11, у другому випадку виключається перший стовпець, покладаємо a1 = a1 – x11, у третьому випадку з подальшого
розгляду виключаються як перший стовпець, так i перший рядок. У зменшеній таким чином транспортній таблиці знаходиться її верхня ліва клітинка (пiвнiчно-захiдний кут), завантажується максимально можливим чином i т. д.
Зрозумiло, що побудований таким чином план перевезень є допустимим розв'язком ТЗЛП. Крiм того, цей план є базисним.
Зауважимо, що при побудові початкового базисного розв'язку методом
пiвнiчно-захiдного кута зовсім не враховуються собівартості перевезень c i j . Тому,
як правило, такий план є далеким від оптимального.
Розглянемо один із методів, де при знаходженні початкового базисного
розв'язку приймаються до уваги собівартості перевезень c i j .
2. Метод мінімального елемента
Ідея методу полягає у тому, щоб максимальним чином завантажити перевезеннями комунікації з мінімальною собівартістю перевезень. Фактично ж
цей метод відрізняється від методу пiвнiчно-захiдного кута лише тим, що на
кожному кроцi побудови початкового базисного розв'язку для завантаження вибирається клітинка з мінімальним значенням c i j .
Метод мінімального елемента в результаті також дає допустимий базисний
розв'язок ТЗЛП.
У таблицях 2.2 та 2.3 наведені початкові базисні розв'язки ТЗЛП, побудовані
за методом пiвнiчно-захiдного кута (невироджений та вироджений).
Наведемо приклад побудови початкового базисного розв'язку методом мінімального елемента (таблиця 2.4).
Таблиця 2.4
|
Q1 |
Q2 |
Q3 |
Q4 |
|
Q5 |
|
a |
|
|
8 |
12 |
4 |
|
9 |
|
10 |
|
|
P1 |
30 |
|
15 |
|
|
15 |
|
60 |
|
P2 |
7 |
5 |
15 |
35 |
3 |
5 |
6 |
40 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
9 |
4 |
6 |
|
12 |
|
7 |
|
|
P3 |
|
80 |
|
|
|
20 |
|
100 |
|
|
5 |
3 |
2 |
|
6 |
|
4 |
|
|
P4 |
|
|
50 |
|
|
|
|
50 |
|
b |
30 |
80 |
65 |
35 |
|
40 |
|
250 |
|
Таблиця 2.2
|
Q1 |
Q2 |
Q3 |
Q4 |
a |
P1 |
3 |
5 |
2 |
|
10 |
P2 |
|
|
8 |
7 |
15 |
P3 |
|
|
|
7 |
7 |
b |
3 |
5 |
10 |
14 |
32 |
-
Таблиця 2.3
Q1
Q2
Q3
Q4
Q5
a
P1
10
10
20
P2
5
15
•
20
P3
8
9
17
b
10
15
15
8
9
57
15.
16.
17.Рудик
18.Рудик
19.Аракелова
20-21. Постановка задачі про найкоротший шлях. Алгоритм методу Мінті.
Розглянемо мережу , що визначається графом g,з означеною на U функцією вартістю Cij , на цій мережі розглянемо також дві фіксовані вершини і1, іs, та довільний шлях ,що з’єднує дві точкі (точкі вершини).
I=I(i1,is)=((i1,is),(i2,i3)…(i5-1,is))(3);
Розглянемо
функцію
Ci=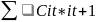 (4)
,яка
інтерпретується
або
як
собі
вартість
перевезення
вантажу
по
шляху
І
або
, як
довжину
шляху
І,
яка
інтерпретується.
(4)
,яка
інтерпретується
або
як
собі
вартість
перевезення
вантажу
по
шляху
І
або
, як
довжину
шляху
І,
яка
інтерпретується.
Задача про найкоротший шлях :Полягає в пошуку шляху (3), що мінімізує цільову функцію(4).Шуканий шлях I*=argminC(I) називається найкоротшим(оптимальним). З формальноної точки зору задача про мінімальний шлях є частковим випадком задачі про оптимальний потік. Для цього розглядається мережа, вершина і1, якої є джерелом одиничної інтенсивності , вершина іs є стоком одиничної інтенсивності , а решта вершин нейтральна . Для розв’язання задачі про найкоротший шлях розроблена значна кількість методів, що дозволяють її розв’язати та враховують її специфіку та одним з таких методів є метод Мінті(метод позначок). Згідно цього методу процес розв’язання задачі складається із скінченного числа елементарних кроків на кожному з яких позначаються вершини в мережі та виділяються деякі, її дуги.
Метод мінті:
Крок 1:Позначається вершина і1(коренева вершина)позначкою hi(1)=0, тоді I(1)={I1} записуємо множину позначених вершин. Нехай після виконання r кроків , ми отримали множину. I(r)={i1,…i2,….}позначених вершин з індексом і(ᶋ), кожні з яких поставлена у відповідність позначка hi(ᶋ).
Крок ṛ+1: Розглянемо множину J(n)={….,iµ,..} непозначених вершин іµ, (іᶋ, іµ) є U, iᶋє І(ṛ), Іµ є J(ṛ), I(ṛ)∩j (r)=0⁄, для кожної з таких дуг знаходимо суму hiᶋ+Ciᶋ*iµ. Виділяємо ті дуги для яких ця сума мінімальна , при чому з декількох дуг , що підлягають виділенню і закінчуються в одній і тій же вершині виділяється лише одна.Позначаємо кінці виділення дуг числом, що = minзначенню hiᶋ+Ciᶋ*iµ; За рахунок позначених вершин , множина I(r)розширюється до множини І(ṛ+1). За побудовою кожній з позначених вершин (окрім кореневої) закінчується одна виділена дуга .Тому рух від вершин Іsвздовж виділених дуг у напрямку протилежному їх орієнтації реалізується однозначно.
ТЕОРЕМА: Побудований Мінті шлях , що з’єднує вершини і1,іsє найкоротшим,при чому C(I*(i1,is))=his.
Зауваження:
1)Сформульований вище алгоритм методу Мінті розрахований на знаходження єдиного найкоротшого шляху, що з’єднує вершини і1,іs, щоб знайти всю множину найкоротших шляхів на кожному кроці слід виділяти всі дуги з мінімальним показником . Навіть якщо декілька з них закінчується в одній і тій же вершині , а при зворотньому русі з вершини іs, вздовж виділених дуг у кожній з вершин слід розглядати всі можливі продовження .
2) Насправді метод Мінті розв’язує більш загальну задачу: Він знаходив найкоротший шлях з кореневої в кожну з позначених вершин.
3) Якщо процес позначення вершин методом Мінті продовжувати до тих пір , поки не припинеться розширення множини позначених вершин , то буде розв’язана задача знаходження найкоротшого шляху з початкової вершини і1 у кожну позначену. Якщо при цьому деяка вершина мережі непопала до числа позначення , то не існує шляху з кореневої вершини в цю вершину.
22-23.Метод Форда-Фалкерсона
Дан
граф
 ,
де А − множина вузлів, В − множина дуг.
Граф G має одне джерело s
і один стік t.
Дуги bij
мають обмежену пропускну здібність.
,
де А − множина вузлів, В − множина дуг.
Граф G має одне джерело s
і один стік t.
Дуги bij
мають обмежену пропускну здібність.
|
(3.1) |
де fij – можливий потік через гілку bij;
Uij – задане значення пропускної здібності для гілки bij.
Величина потоку з джерела не обмежена і в кожному проміжному вузлі виконується умова збереження потоку.
|
(3.2) |
Задача складається у визначенні дугових потоків fij таких, щоб загальний потік з джерела s в стік t був максимальним:
|
(3.3) |
Задача вирішується за допомогою ітераційної процедури розстановки поміток вузлів. Кожна помітка вказує величину потоку та його джерело, і може бути як позитивною, так і негативною.
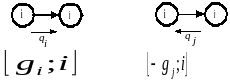
де gi , gj – кількість одиниць потоку.
Позитивна помітка збільшує потік по гілці bij, але так, щоб сумарний потік не перевищував Uij; негативна помітка зменшує потік по гілці bij, але так, щоб він не став від’ємним.
Вузли помічаються послідовно від 1 до n.
Якщо
вузол ai
помічений, то aj
можна помітити з нього по прямій гілці
на величину не більшу, за
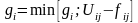 ,
а по зворотній гілці на величину
,
а по зворотній гілці на величину
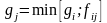 .
.
На
кожній ітерації джерело помічається
міткою
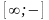 і розставляються мітки інших вузлів по
одному із шляхів з джерела до стоку.
Коли доходить черга до стоку, йому
приписується мітка
і розставляються мітки інших вузлів по
одному із шляхів з джерела до стоку.
Коли доходить черга до стоку, йому
приписується мітка
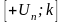 .
Тобто потік в мережі можна збільшити
на Un
; після чого всім дугам шляху, що
розглядається, приписується
.
Тобто потік в мережі можна збільшити
на Un
; після чого всім дугам шляху, що
розглядається, приписується
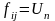 .
.
Потім всі мітки стираються і переходять до наступної ітерації.
Алгоритм закінчує роботу, якщо жоден вузол мережі вже не може бути поміченим.
Теорема
про максимальний потік і мінімальний
розріз.
Нехай
буде заданий граф
.
Розіб’ємо множину А
на дві непересічні підмножини
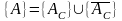 ,
так щоб джерело і стік графа не знаходились
в одної підмножині. Все дуги, що з’єднують
ці дві підмножини, утворюють множину
,
так щоб джерело і стік графа не знаходились
в одної підмножині. Все дуги, що з’єднують
ці дві підмножини, утворюють множину
 .
.
Множина дуг, яку необхідно вилучити з графа, щоб порушити його зв’язність, називається перетином. Тобто і є перетин.
Кількість дуг в перетині називається рангом перетину, а сумарна пропускна здібність всіх дуг перетину – розрізом.
Очевидним являється тий факт, що потік з джерела в стік буде обмежений зверху розрізом. Більш того, максимальний потік із джерела в стік дорівнює мінімальному розрізу, що розділяє джерело і стік.
Практичне значення даної теореми наступне: послідовно перебираючи всі розрізи, що розділяють джерело і стік, і обираючи мінімальний з них, можна визначити максимальний потік. Однак, визначити дугові потоки дана теорема не дозволяє. Ця теорема корисна для аналізу вузьких місць в мережі.
Приклад 3. Дан граф
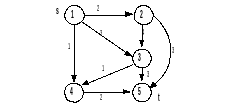
1 ітерація. Шлях: 1-3-5
Помітки:
Потоки
в гілках:
Загальний
потік збільшився на
 =2
=2
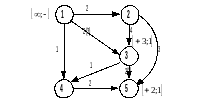
2 ітерація. Шлях: 1-2-3-4-5
Помітки:
Потоки
в гілках:
Загальний потік збільшився на =1
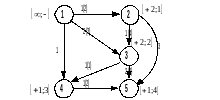
3 ітерація. Шлях: 1-2-5
Помітки:
Потоки
в гілках:
Загальний потік збільшився на =1
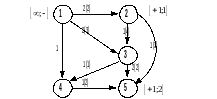
4 ітерація. Шлях: 1-3-2-5
Помітки:

Потоки
в гілках:
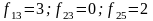
Загальний потік збільшився на =1
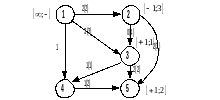
5 ітерація. Шлях: 1-4-5
Помітки:
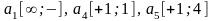
Потоки
в гілках:
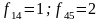
Загальний потік збільшився на =1
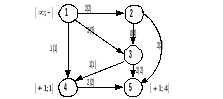
6 ітерація. Ще будь-який шлях вибрати неможливо.
Максимальний потік в мережі, поданий графом, що розглядається, дорівнює сумі приростів потоків на кожній ітерації, тобто V = 6.
В
даному прикладі можна визначити
максимальний потік, використовуючи
теорему про максимальний потік і
мінімальний розріз, яким являється
розріз
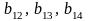 .
.
24. Метод відтинання. Алгоритм Гоморі
Загальна
задача лінійного дискретного цілочисельного
програмування має вигляд:
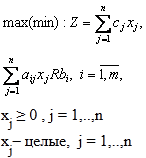 Задача
називається повністю целочисленной
завданням лінійного програмування,
тому що на всі змінні покладено умова
цілочисельності. Коли ця умова стосується
лише деяким змінним, завдання називається
частково целочисленной. Нехай дана
задача повністю цілочисельного лінійного
програмування. Алгоритм методу відсікань
складається з наступних етапів: 1)
вирішується ЗЛП з відкинутими умовою
цілочисельності; якщо вона не розв'язана,
то завдання теж рішення не має; 2) якщо
умова цілочисельності виконується по
всім змінним, то знайдене рішення є
рішення задачі; 3) інакше будується
додаткове відсікають обмеження,
включається в систему обмежень і на
етап 1. Для рішення повністю целочисленной
завдання ЛП Гоморі запропоновано робити
кожен раз на етапі 3 додаткове обмеження
для нецілої змінної з найбільшою дробовою
частиною. Припустимо, що завдання з
відкинутим умовою цілочисельності
вирішена. Розглянемо i-й рядок оптимальної
симплексного таблиці, якій відповідає
неціле рішення β i базисної змінної xi
Нехай R - безліч індексів j, які відповідають
небазисним змінним. Тоді мінлива xi може
бути виражена через небазисних змінних
xj:
Задача
називається повністю целочисленной
завданням лінійного програмування,
тому що на всі змінні покладено умова
цілочисельності. Коли ця умова стосується
лише деяким змінним, завдання називається
частково целочисленной. Нехай дана
задача повністю цілочисельного лінійного
програмування. Алгоритм методу відсікань
складається з наступних етапів: 1)
вирішується ЗЛП з відкинутими умовою
цілочисельності; якщо вона не розв'язана,
то завдання теж рішення не має; 2) якщо
умова цілочисельності виконується по
всім змінним, то знайдене рішення є
рішення задачі; 3) інакше будується
додаткове відсікають обмеження,
включається в систему обмежень і на
етап 1. Для рішення повністю целочисленной
завдання ЛП Гоморі запропоновано робити
кожен раз на етапі 3 додаткове обмеження
для нецілої змінної з найбільшою дробовою
частиною. Припустимо, що завдання з
відкинутим умовою цілочисельності
вирішена. Розглянемо i-й рядок оптимальної
симплексного таблиці, якій відповідає
неціле рішення β i базисної змінної xi
Нехай R - безліч індексів j, які відповідають
небазисним змінним. Тоді мінлива xi може
бути виражена через небазисних змінних
xj:
![]() -
не целое. Обозначим наибольшую целую
часть числа a, его не превосходящую,
через [a], ( a≥[a]), а дробную положительную
часть – через {a} Очевидно a = [a] + {a}.
Например, если a=4,7 то [a] = 4, {a} = 0,7, если a
=-8,6, то [a] = -9, {a} = 0,4. Выразим базисную
переменную xi в виде суммы целой и дробной
частей.
-
не целое. Обозначим наибольшую целую
часть числа a, его не превосходящую,
через [a], ( a≥[a]), а дробную положительную
часть – через {a} Очевидно a = [a] + {a}.
Например, если a=4,7 то [a] = 4, {a} = 0,7, если a
=-8,6, то [a] = -9, {a} = 0,4. Выразим базисную
переменную xi в виде суммы целой и дробной
частей.
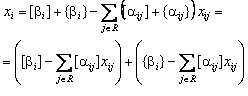 Вираз
в лівих круглих дужках (4.6) ціле число,
і щоб xj було цілим, необхідно, щоб
вираження у правих круглих дужках (4.6)
теж було цілим. коли вираз
Вираз
в лівих круглих дужках (4.6) ціле число,
і щоб xj було цілим, необхідно, щоб
вираження у правих круглих дужках (4.6)
теж було цілим. коли вираз
![]() буде
цілим? Так як 0 ≤
буде
цілим? Так як 0 ≤
![]() то
Li буде цілим числом, якщо
то
Li буде цілим числом, якщо
![]() тобто
тобто
![]() .Співвідношення
визначає правильне відсікання Гоморі.
Завдання не буде мати повністю
цілочисельного рішення, якщо зустрінеться
в симплекс-таблице рівняння таке, що βi
дробове число, а αij-цілі.
.Співвідношення
визначає правильне відсікання Гоморі.
Завдання не буде мати повністю
цілочисельного рішення, якщо зустрінеться
в симплекс-таблице рівняння таке, що βi
дробове число, а αij-цілі.
25. Частково цiлочисельнi задачі лінійного програмування. Другий метод Гоморi
Другий метод Гоморi призначається для розв'язування частково (зокрема,
повнiстю) цiлочисельних ЗЛП ( ЧЦЗЛП ):
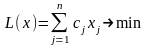 (4.17)
(4.17)
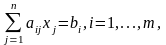 (4.18)
(4.18)
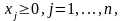 (4.19)
(4.19)
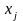 -ціле,
j=1,…,p
-ціле,
j=1,…,p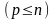 (4.20)
(4.20)
Метод розв'язування задачі (4.17) – (4.20) грунтується на тій же ідеї, що i метод розв'язування ПЦЗЛП. А саме : розв'язується допоміжна ЗЛП (4.17) – (4.19), що одержується з вихідної відкиданням умови цiлочисельностi (4.20). Якщо ця задача розв'язку не має, то, очевидно, i вихідна ЧЦЗЛП не має розв'язку. Якщо ж ЗЛП (4.17) – (4.19) має розв'язок, то він аналізується на допустимість для задачі (4.17) – (4.20). Якщо знайдений оптимальний розв'язок є цiлочисельним ( у розумінні умов (4.20)), то він одночасно є оптимальним i для задачі (4.17) – (4.20). Iнакше від розв'язаної ЗЛП переходять до нової допоміжної ЗЛП додаванням лінійного обмеження, яке задовольняють цiлочисельнi розв'язки вихідної ЧЦЗЛП, але не задовольняє одержаний нецiлочисельний розв'язок вихідної ЗЛП. Це
додаткове обмеження визначає деяку вiдтинаючу площину i називається
правильним вiдтином. Додавання нових правильних вiдтинiв відбувається доти, поки на деякому кроцi не буде одержано цiлочисельний розв'язок допоміжної задачі, що є, очевидно, оптимальним розв'язком ЧЦЗЛП.
Нехай на останній iтерацiї симплекс-методу при розв'язуванні допоміжної
ЗЛП її непрямі обмеження набули вигляду :
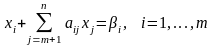
i,
отже,
її
розв'язком
є
n-вимiрний
вектор
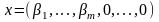 .
.
Нехай
існує
номер
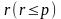 такий,
що
такий,
що
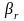 —
дробове
число.
Тоді
правильний
—
дробове
число.
Тоді
правильний
вiдтин у другому методі Гоморi будується згідно наступної теореми, яку ми наводимо без доведення.
Теорема 4.2. Лiнiйне обмеження
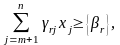 або,
що
рiвносильно,
або,
що
рiвносильно,
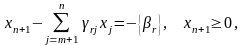
де
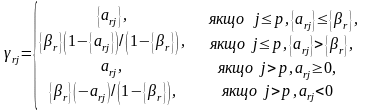 (4.23)
(4.23)
a
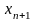 -
додаткова
змінна,
є
правильним
вiдтином
для
ЧЦЗЛП
(4.17)
–
(4.20).
-
додаткова
змінна,
є
правильним
вiдтином
для
ЧЦЗЛП
(4.17)
–
(4.20).
Зауважимо, що якщо r в обмеженні (4.22) є індекс першої нецiлочисельної змінної серед перших p змінних, то алгоритм другого методу Гоморi, що формулюється нижче, є скiнченним.
Алгоритм другого методу Гоморi
1. Розв'язуємо допоміжну ЗЛП (4.17) – (4.19). Нехай x (0 ) — її оптимальний розв'язок. Якщо оптимального розв'язку не існує, то вихідна ЧЦЗЛП (4.17) – (4.20) також не має розв'язку.
2. Нехай на s-й iтерацiї розв'язана допоміжна ЗЛП, що має M обмежень та N змінних, x ( s ) — її оптимальний розв'язок. Будемо вважати, що канонічні обмеження останньої iтерацiї, що визначають x ( s ), мають вигляд :
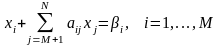
Звiдси
N-вимiрний
вектор
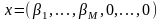 .
.
3. Якщо
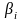 ,
i
=
1,...,p,
—
цілі,
то
кінець
:
x
(
s
)
є
оптимальним
розв'язком
,
i
=
1,...,p,
—
цілі,
то
кінець
:
x
(
s
)
є
оптимальним
розв'язком
вихідної ЧЦЗЛП. Якщо існує хоча б одне i таке, що — дріб ( i = 1,...,p ), то
переходимо до пункту 4.
4. Знаходимо r=min{ i }, де мінімум береться по всіх i ( i=1,...,p ) таких, що i —
дріб, i будуємо додаткове обмеження за формулами (4.22), (4.23) при m = M, n = N.
5. Розширюємо симплекс-таблицю за рахунок ( M+1)-го рядка ( додаткове обмеження) та ( N+1)-го стовпця, що відповідає додатковій змінній xN+1.
6. Розв'язуємо розширену таким чином ЗЛП двоїстим симплекс-методом i
переходимо до пункту 2, заміняючи s на s +1. Якщо при цьому на деякій iтерацiї двоїстого симплекс-методу одна з додаткових змінних повторно стає базисною, то з подальшого розгляду виключаються відповідні їй рядок та стовпець.
26. Третiй метод Гоморi
Розглядаємо ПЦЗЛП :
(4.14)
(4.25)
(4.26)
-ціле, j=1,…,n (4.27)
Нехай непрямі обмеження ЗЛП (4.24) – (4.26), наприклад, у базисі A 1,...,A m
приведені до майже канонічного вигляду :
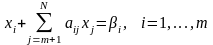
де
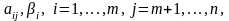 —
цілі
i
симплекс-рiзницi
—
цілі
i
симплекс-рiзницi
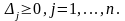 Якщо
Якщо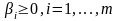 ,
i
=
1,...,m
,
то
обмеження
визначають
оптимальний
розв'язок
задачі
(4.24)
–
(4.27),
iнакше
визначається
деякий
цiлочисельний
МДБР
вихідної
ЗЛП.Можна
було
б,
звичайно,
вибрати
один
з
індексів
i,
для
якого
i
<
0,
i
виконати
iтерацiю
двоїстого
симплекс-методу.
Проте
у
цьому
випадку
цiлочисельнiсть
параметрів
нової
симплекс-таблицi
була
б,
взагалі
кажучи,
порушена
через
необхідність
,
i
=
1,...,m
,
то
обмеження
визначають
оптимальний
розв'язок
задачі
(4.24)
–
(4.27),
iнакше
визначається
деякий
цiлочисельний
МДБР
вихідної
ЗЛП.Можна
було
б,
звичайно,
вибрати
один
з
індексів
i,
для
якого
i
<
0,
i
виконати
iтерацiю
двоїстого
симплекс-методу.
Проте
у
цьому
випадку
цiлочисельнiсть
параметрів
нової
симплекс-таблицi
була
б,
взагалі
кажучи,
порушена
через
необхідність
ділення на ведучий елемент перетворення. Цiлочисельнiсть нової nтаблиці гарантується лише тоді, коли ведучий елемент дорівнює –1.
Виявляється,що можна побудувати додаткове обмеження, якому задовольняють всі цiлочисельнi розв'язки задачі (4.24) – (4.27) i яке разом з тим визначає ведучий рядок перетворення, що має ведучий елемент –1. Будується
воно
за
l-м
обмеженням
системи
(4.28
),
для
якого
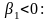
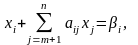 (4,29)
(4,29)
Якщо серед обмежень (4.28) є декілька з від'ємною правою частиною, то l
вибирається, як правило, з умови
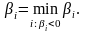
Подiлимо
обидві частини (4.29) на
довільне число a
>
0 I
 запишемо
одержаний
результат
у
вигляді
:
запишемо
одержаний
результат
у
вигляді
:
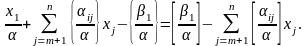 (4.30)
(4.30)
Лiва
частина
(4.30)
при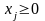 ,
j
=
1,...,n,
являє
собою
різницю
двох
величин
,
j
=
1,...,n,
являє
собою
різницю
двох
величин
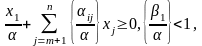
тобто строго більша –1.Отже,права частина, будучи цілим числом при цiлочисельних x j , задовольняє умову
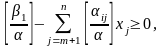 (4.31)
(4.31)
яка є вірною для будь-якого допустимого розв'язку задачі (4.24) – (4.27).
Уводячи додаткову змінну x n+1 , перепишемо (4.31) у вигляді
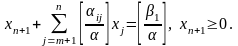 (4.32)
(4.32)
Очевидно,
що
з
від'ємності
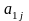 випливає
від'ємність
[
випливає
від'ємність
[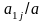 ]
i
навпаки.
Тому
[
]
i
навпаки.
Тому
[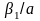 ]
<
0
i
серед
чисел
[
]
є
від'ємні,
тобто
рядок
таблиці,
що
визначається
новим
обмеженням
(4.32),
може
бути
прийнятий
за
ведучий
для
наступного
симплексного
перетворення.
Разом
з
тим
при
]
<
0
i
серед
чисел
[
]
є
від'ємні,
тобто
рядок
таблиці,
що
визначається
новим
обмеженням
(4.32),
може
бути
прийнятий
за
ведучий
для
наступного
симплексного
перетворення.
Разом
з
тим
при
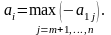
кожному від'ємному , j = m +1,...,n, відповідає [ ] = –1, тобто ведучий
елемент цього перетворення явно дорівнює –1.
Отже, розширюємо наявну симплекс-таблицю за рахунок (m+1)-го рядка з
елементами [ ] (елементи, що відповідають базисним змінним, рівні нулю) та
одиничного стовпця A n+1, що відповідає додатковій змінній . Потiм виконується симплекс-перетворення з (m+1)-м ведучим рядком I ведучим стовпцем, що вибирається за правилами двоїстого симплекс-методу. Тоді нова симплекс-таблиця буде повністю цiлочисельною.Описана послідовність дій складає окрему iтерацiю алгоритму третього методу Гоморi. Iтерацiї виконуються доти, поки не буде отримана симплекс-таблиця, в якій усі праві частини невід'ємні, або є рядок з від'ємною правою частиною i невід'ємними рештою елементів. У першому випадку ПЦЗЛП розв'язана, у другому — її обмеження є суперечливими. Якщо на будь-якiй iтерацiї одна з додаткових змінних переходить з небазисних у базисні, то відповідні їй рядок i стовпець симплекс-таблицi викреслюються з подальшого розгляду.
Алгоритм третього методу Гоморi
1. Зводимо ЗЛП (4.24) – (4.26) до МКЗЛП з цiлочисельними коефіцієнтами,
що
визначає
цiлочисельний
МДБР
x
(
0
),
для
якого
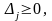 ,
j
=
1,...,n.
,
j
=
1,...,n.
2. Нехай на s-й iтерацiї одержана повністю цiлочисельна МКЗЛП з непрямими обмеженнями виду
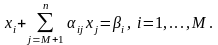
що
визначає
цiлочисельний
N-вимiрний
МДБР
x
(
s
)=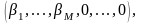 для
якого
для
якого
, j = 1,...,N.
3.
Якщо
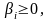 i
=
1,...,M,
то
кінець
:
x
(
s
)
є
оптимальним
розв'язком
ПЦЗЛП.
i
=
1,...,M,
то
кінець
:
x
(
s
)
є
оптимальним
розв'язком
ПЦЗЛП.
4. Якщо
для
деякого
i,
такого,
що
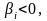
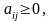 j
=
1,...,N,
то
кінець
:
ПЦЗЛП
j
=
1,...,N,
то
кінець
:
ПЦЗЛП
(4.24) – (4.27) не має допустимих розв'язкiв. Якщо таких i немає, то
5. Знаходимо індекс l з умови: де мінімум визначається на
множині
тільки
тих
i,
для
яких
<
0.
Знаходимо
=
max
(
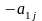 ),
де
максимум
),
де
максимум
визначається на множині j = M +1,...,N, i будуємо додаткове обмеження (4.32) при
m= M та n= N.
6. Розширюємо симплекс-таблицю за рахунок ( M +1)-го рядка (додаткове обмеження) та ( N +1)-го стовпця, що відповідає додатковій змінній xN+1.
7. Знаходимо
індекс
k
з
умови:
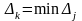 ,
де
мінімум
визначається
на
множині
тільки
тих
j
,
для
яких
,
де
мінімум
визначається
на
множині
тільки
тих
j
,
для
яких
 ,
j
<
0.
Переходимо
до
нового
цiлочисельного
МДБР
x
(
s
+1),
виконуючи
симплекс-перетворення
з
ведучими
рядком
(
M+1)
i
стовпцем
k
.
Якщо
k
—
індекс
однієї
з
додаткових
змінних,
то
переходимо
до
пункту
,
j
<
0.
Переходимо
до
нового
цiлочисельного
МДБР
x
(
s
+1),
виконуючи
симплекс-перетворення
з
ведучими
рядком
(
M+1)
i
стовпцем
k
.
Якщо
k
—
індекс
однієї
з
додаткових
змінних,
то
переходимо
до
пункту
8, iнакше — до пункту 3, заміняючи s на s +1, M на M +1, N на N +1.
8. Виключаємо з подальшого розгляду (викреслюємо) k-й стовпець та ( M +1)-й (останній) рядок симплекс-таблицi, перенумеровуємо решту додаткових змінних для збереження неперервної нумерації всіх змінних задачі i переходимо до пункту 3, заміняючи s на s +1.
Звертаючи увагу на пункт 1 алгоритму, зауважимо, що інколи побудова цiлочисельної симплекс-таблицi з невід'ємними значеннями симплекс-рiзниць не вимагає обчислень. У загальному ж випадку цей етап зводиться до застосування цього ж методу до деякої допоміжної задачі, причому на одній з його iтерацiй може виявитися неможливість побудови потрібної вихідної таблиці. Враховуючи це,
навряд чи варто застосовувати цей метод до розв'язування задач, у яких зміст вихідної таблиці не є очевидним
27.Стельмах
28.Стельмах
29-32.
Задачі теорії гри
Теорія ігор вперше була систематично викладена Нейманом і Моргенштерном та оприлюднена лише 1944 року в монографії «Теорія ігор і економічної поведінки», хоча окремі результати були опубліковані ще в 20-х роках. Нейман і Моргенштерн написали оригінальну книгу, яка містила переважно економічні приклади, оскільки економічні задачі простіше за інші описати за допомогою чисел. Під час другої світової війни і одразу після неї теорією ігор серйозно зацікавились військові, які одразу побачили в ній математичний апарат для дослідження стратегічних проблем і підготовки рішень. Потім головна увага знову була звернута до економічних проблем. Нині сфера застосування теорії ігор значно розширилась. Так, у соціальних науках апарат теорії ігор застосовується у психології для аналізу торгових угод та переговорів, а також для вивчення принципів формування коаліцій тощо.
Основні поняття теорії ігор
У попередніх розділах описані такі задачі математичного програмування, де рішення на основі розрахованого оптимального плану приймає лише один суб'єкт, що має чітко визначену мету. Відомо, що будь-яка економічна система не функціонує ізольовано, а на певних етапах своєї діяльності вступає в різні економічні відносини з іншими суб'єктами господарювання. Оптимальний план за наведеними вище математичними моделями визначався, виходячи з інтересів тільки однієї сторони економічних відносин, не враховуючи можливі варіанти дій інших сторін.
У даному розділі розглядаються ситуації з кількома учасниками, коли значення цільової функції для кожного учасника залежить не лише від його власної поведінки, але і від дій інших суб'єктів.
За умов ринкової економіки все частіше мають місце конфліктні ситуації, коли два або більше колективів (індивідуумів) мають протилежні цілі та інтереси, причому результат дії кожної із сторін залежить і від дії супротивника. Класичним прикладом конфліктної ситуації в економіці є відношення продавець — покупець (монополія — монопсонія). Складніші ситуації виникають, коли в суперечці інтересів беруть участь об'єднання чи коаліції.
Зазначимо, що не завжди учасники ігрової ситуації мають протилежні цілі. Наприклад, дві фірми, які надають однакові послуги, можуть об'єднуватися з метою спільного протистояння більшому супернику.
Часто однією із сторін конфлікту є природні процеси чи явища, наприклад, погода, тобто маємо гру людини з природою. Погодними умовами людина практично не може керувати, але вона має змогу пристосовуватися до її постійних змін. Безліч подібних ситуацій можна зустріти і в інших сферах людської діяльності: біології, психології, політології тощо.
Теорія ігор — це математичний апарат, що розглядає конфліктні ситуації, а також ситуації спільних дій кількох учасників. Завдання теорії ігор полягає у розробленні рекомендацій щодо раціональної поведінки учасників гри.
Реальні конфліктні ситуації досить складні і обтяжені великою кількістю несуттєвих чинників, що ускладнює їх аналіз, тому на практиці будують спрощені моделі конфліктних ситуацій, які називають іграми.
Характерними рисами математичної моделі ігрової ситуації є наявність, по-перше, кількох учасників, яких називають гравцями, по-друге, опису можливих дій кожної із сторін, що називаються стратегіями, по-третє, визначених результатів дій для кожного гравця, що подаються функціями виграшу. Задачею кожного гравця є знаходження оптимальної стратегії, яка за умови багатократного повторення гри забезпечує даному гравцю максимально можливий середній виграш.
Існує дуже багато різних ігор. Прикладом «гри» в буквальному розумінні цього слова, передусім, є спортивна, карточна гра, шахи тощо. Від реальної конфліктної ситуації гра відрізняється не лише спрощеною формою, а також наявністю певних правил, за якими мають діяти її учасники. Дослідження таких формалізованих ігор звичайно не може дати чітких рекомендацій для реальних умов, проте є найзручнішим об'єктом для вивчення конфліктних ситуацій і оцінки можливих рішень з різних поглядів. Розраховані на основі ігрових моделей оптимальні плани не визначають єдино правильне рішення за складних реальних умов, проте слугують математично обґрунтованою підставою для прийняття таких рішень.
Класифікація ігор проводиться відповідно до вибраного критерію. Ігри можуть розрізнятися залежно від кількості гравців, кількості стратегій, властивостей функцій виграшу, можливостей взаємодії між гравцями.
Якщо в грі беруть участь два гравці, то така гра називається парною (грою двох осіб). Часто у грі беруть участь багато сторін, тоді гра є множинною.
Залежно від кількості стратегій розрізняють скінченні та нескінченні ігри. Якщо кожен гравець має скінченну кількість стратегій, то гра — скінченна, в іншому разі — нескінченна.
Якщо виграш одного гравця дорівнює програшу іншого, то маємо гру з нульовою сумою. Такі ігри характеризуються протилежними інтересами сторін, тобто ситуацією конфлікту. Інші ігри — з ненульовою сумою, виникають як за умов конфліктної поведінки гравців, так і за їх узгоджених дій.
За можливості поєднання інтересів гравців та домовленості між ними про вибір стратегій можна казати про кооперативну гру, коли ж гравці не мають можливості чи не бажають координувати свої дії, то гра називається некооперативною.
Матричні ігри двох осіб
Найчастіше розглядається гра з двома гравцями, в якій виграш однієї сторони дорівнює програшу іншої, а сума виграшів обох сторін дорівнює нулю, що в теорії ігор називають грою двох осіб з нульовою сумою. Подібна ситуація є типовою у практичній діяльності менеджерів, маркетологів, спеціалістів рекламних служб, які щоденно приймають рішення за умов гострої конкуренції, неповноти інформації тощо. Основною метою розв'язування задач цього класу є розроблення рекомендацій щодо вибору оптимальних стратегій конфліктуючих сторін на основі застосування методичних підходів теорії ігор.
Отже,
маємо два гравці А і В (гра двох осіб з
нульовою сумою). Кожний
гравець вибирає одну із можливих
стратегій: позначимо
стратегії
гравця А -
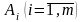 ,
стратегії
гравця В -
,
стратегії
гравця В -
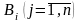 .
.
Результати (плата) за всіма можливими варіантами гри задаються спеціальними функціями, які залежать від стратегій гравців, як правило, у вигляді платіжної матриці.
Нехай
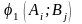
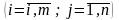 виграш гравця А,
виграш гравця А,
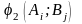 виграш
гравця В.
виграш
гравця В.
Оскільки
гра з нульовою сумою, то
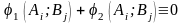 .
Тоді
в
разі,
якщо
.
Тоді
в
разі,
якщо
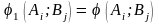 ,
то
,
то
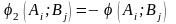 .
.
Отже,
мета гравця А — максимізувати величину
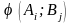 ,
а
гравця
В — мінімізувати її. Нехай
,
а
гравця
В — мінімізувати її. Нехай
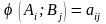 ,
тобто маємо матрицю
А:
,
тобто маємо матрицю
А:
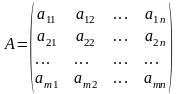 ,
,
де
рядки відповідають стратегіям
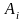 ,
а
стовпці — стратегіям
,
а
стовпці — стратегіям
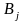 .
.
Матриця
А називається платіжною,
а
також матрицею
гри.
Елемент
цієї матриці
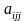 —
це виграш гравця А, якщо він вибрав
стратегію
,
а
гравець В — стратегію
.
—
це виграш гравця А, якщо він вибрав
стратегію
,
а
гравець В — стратегію
.
Із багатьох критеріїв, які пропонуються теорією ігор для вибирання раціональних варіантів рішень, найпоширенішим є песимістичний критерій мінімаксу-максиміну. Суть цього критерію у наступному.
Нехай
гравець А вибрав стратегію
,
тоді у найгіршому разі він
отримає виграш, що дорівнює
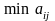 ,
тобто
навіть тоді, якщо гравець В і знав би
стратегію гравця А. Передбачаючи таку
можливість, гравець А має вибрати таку
стратегію, щоб максимізувати
свій мінімальний виграш, тобто
,
тобто
навіть тоді, якщо гравець В і знав би
стратегію гравця А. Передбачаючи таку
можливість, гравець А має вибрати таку
стратегію, щоб максимізувати
свій мінімальний виграш, тобто
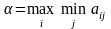 .
.
Така
стратегія гравця А позначається
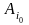 і
має назву максимінної,
а
величина гарантованого виграшу цього
гравця називається
нижньою
ціною гри.
і
має назву максимінної,
а
величина гарантованого виграшу цього
гравця називається
нижньою
ціною гри.
Гравець
В, який програє суми у розмірі елементів
платіжної матриці, навпаки має вибрати
стратегію, що мінімізує його максимально
можливий програш за всіма варіантами
дій гравця А. Стратегія гравця В
позначається через
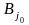 і
називається мінімаксною,
а
величина його програшу — верхньою
ціною
гри,
тобто
і
називається мінімаксною,
а
величина його програшу — верхньою
ціною
гри,
тобто
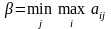 .
.
Оптимальний розв'язок цієї задачі досягається тоді, коли жодній стороні невигідно змінювати вибрану стратегію, оскільки її супротивник може у відповідь вибрати іншу стратегію, яка забезпечить йому кращий результат.
Якщо
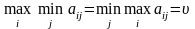 ,
тобто,
якщо
,
тобто,
якщо
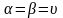 ,
то гра називається цілком
визначеною.
В
такому разі виграш гравця А (програш
гравця В) називається значенням
гри
і
дорівнює елементу матриці
,
то гра називається цілком
визначеною.
В
такому разі виграш гравця А (програш
гравця В) називається значенням
гри
і
дорівнює елементу матриці
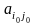 .
.
Цілком визначені ігри називаються іграми з сідловою точкою, а елемент платіжної матриці, значення якого дорівнює виграшу гравця А (програшу гравця В) і є сідловою точкою. В цій ситуації оптимальним рішенням гри для обох сторін є вибір лише однієї з можливих, так званих чистих стратегій — максимінної для гравця А та мінімаксної для гравця В, тобто якщо один із гравців притримується оптимальної стратегії, то для другого відхилення від його оптимальної стратегії не може бути вигідним.
Як правило, задачі теорії ігор, що моделюють реальні ситуації, мають значну розмірність. Тому важливим моментом дослідження платіжної матриці є способи її скорочення. Скоротити матрицю можна, якщо вилучити стратегії, про які наперед відомо, що вони є невигідними або повторюють одна одну.
Стратегії,
яким відповідають однакові значення
платіжної матриці ( тобто матриця
містить однакові рядки (стовпці) )
називаються
дублюючими.
Якщо
всі елементи
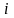 -го
рядка (стовпця) платіжної
матриці перевищують значення елементів
-го
рядка (стовпця) платіжної
матриці перевищують значення елементів
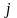 -го
рядка (стовпця),
то кажуть, що
-та
стратегія гравця А (гравця В) є домінуючою
над
-ою.
-го
рядка (стовпця),
то кажуть, що
-та
стратегія гравця А (гравця В) є домінуючою
над
-ою.
Для спрощення розрахунків дублюючі та ті стратегії, для яких існують домінуючі, вилучають з платіжної матриці.
Гра зі змішаними стратегіями
Скінченні
ігри, як правило, не мають сідлової
точки. Якщо гра не
має сідлової точки, тобто
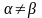 і
і
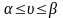 , то максимінно-мінімаксні
стратегії не є оптимальними, тобто
кожна із сторін може
покращити свій результат, вибираючи
інший підхід. Оптимальний
розв'язок такої гри знаходять шляхом
застосування змішаних
стратегій,
які
є певними комбінаціями початкових
«чистих»
стратегій. Тобто змішана стратегія
передбачає використання
кількох «чистих» стратегій з різною
частотою.
, то максимінно-мінімаксні
стратегії не є оптимальними, тобто
кожна із сторін може
покращити свій результат, вибираючи
інший підхід. Оптимальний
розв'язок такої гри знаходять шляхом
застосування змішаних
стратегій,
які
є певними комбінаціями початкових
«чистих»
стратегій. Тобто змішана стратегія
передбачає використання
кількох «чистих» стратегій з різною
частотою.
Ймовірності (або частоти) вибору кожної стратегії задаються відповідними векторами:
для
гравця А – вектор
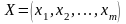 ,
де
,
де
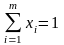 ;
;
для
гравця В – вектор
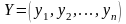 ,
де
,
де
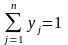 .
.
Очевидно,
що
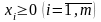 ;
;
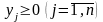 .
.
Виявляється, що коли використовуються змішані стратегії, то для кожної скінченної гри можна знайти пару стійких оптимальних стратегій. Існування такого розв'язку визначає теорема, яку наведемо без доведення.
Теорема (основна теорема теорії ігор). Кожна скінченна гра має, принаймні, один розв'язок, можливий в області змішаних стратегій.
Нехай маємо скінченну матричну гру з платіжною матрицею
.
Оптимальні
змішані стратегії гравців А і В за
теоремою визначають
вектори
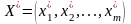 і
і
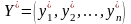 ,
що
дають змогу
отримати виграш:
.
,
що
дають змогу
отримати виграш:
.
Використання
оптимальної змішаної стратегії гравцем
А має забезпечувати
виграш на рівні, не меншому, ніж ціна
гри за умови
вибору гравцем В будь-яких стратегій.
Математично ця умова записується
так:
 .
.
З
другого боку, використання оптимальної
змішаної стратегії гравцем В має
забезпечувати за будь-яких стратегій
гравця А програш,
що не перевищує ціну гри
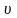 ,
тобто:
,
тобто:
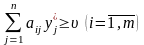 .
.
Ці співвідношення використовуються для знаходження розв'язку гри.
Зауважимо, що в даному разі розраховані оптимальні стратегії завжди є стійкими, тобто якщо один з гравців притримується своєї оптимальної змішаної стратегії, то його виграш залишається незмінним і дорівнює ціні гри незалежно від того, яку із можливих змішаних стратегій вибрав інший гравець.
Геометрична інтерпретація гри теорії гри
Найпростішим випадком скінченої гри є парна гра, коли у кожного учасника є дві стратегії (табл. 8.4.1).
Таблиця 8.4.1.
|
|
|
|
|
|
|
|
|
Розглянемо
випадок, коли гра не має сідловок точки.
Отже,
.
Необхідно знайти змішані стратегії та
ціну гри. Позначимо шукані значення
ймовірностей застосування «чистих»
стратегій гравця А через
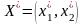 ,
а для гравця В – через
,
а для гравця В – через
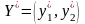 .
.
Згідно з основною теоремою теорії ігор, якщо гравець А притримується своєї оптимальної стратегії, то виграш дорівнюватиме ціні гри. Отже, якщо гравець А притримуватиметься своєї оптимальної стратегії , то:
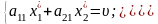 (8.4.1)
(8.4.1)
Оскільки
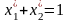 ,
то
,
то
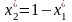 .
Підставивши цей вираз у систему рівнянь
(8.4.1), отримаємо:
.
Підставивши цей вираз у систему рівнянь
(8.4.1), отримаємо:
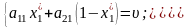 .
.
Розв’язавши
дане рівняння відносно невідомого
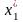 ,
маємо:
,
маємо:
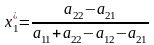 ,
тоді
,
тоді
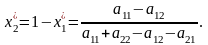
Провівши аналогічні міркування стосовно гравця В, маємо:
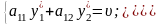 (8.4.2.)
(8.4.2.)
Оскільки
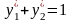 ,
то
,
то
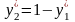 .
.
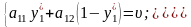 .
.
Розв’язавши
це рівняння відносно невідомого
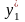 ,
маємо:
,
маємо:
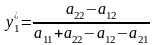 ,
тоді
,
тоді
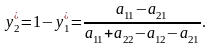
Ціну
гри
знаходять, підставляючи значення
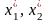 (або
(або
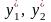 )
в будь-яке з рівнянь (8.4.1) або (8.4.2):
)
в будь-яке з рівнянь (8.4.1) або (8.4.2):
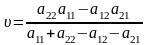 .
.
Задача
8..4.1.
Знайти розв’язок гри, яка задана
матрицею
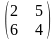 ,
дати геометричну інтерпретацію цього
розв’язку.
,
дати геометричну інтерпретацію цього
розв’язку.
Розв’язання.
Перевіримо наявність сідлової точки
в даній матриці. Для цього знайдемо
мінімальні елементи в кожному рядку
(2 і 4) й максимальні елементи в кожному
з стовбців (6 і 5). Отже, нижня ціна гри
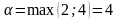 ,
а верхня ціна гри
,
а верхня ціна гри
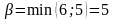 .
Оскільки
.
Оскільки
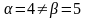 ,
то розв’язком гри є змішані оптимальні
стратегії, а ціна гри
знаходиться в межах
,
то розв’язком гри є змішані оптимальні
стратегії, а ціна гри
знаходиться в межах
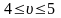 .
.
Припустимо,
що для гравця А стратегія задається
вектором
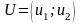 .
Тоді при застосуванні гравцем В чистої
стратегії В1
або В2
гравець А отримає середній виграш,
який дорівнює ціні гри, тобто
.
Тоді при застосуванні гравцем В чистої
стратегії В1
або В2
гравець А отримає середній виграш,
який дорівнює ціні гри, тобто
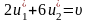 (при
стратегії В1),
(при
стратегії В1),
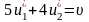 (при
стратегії В2).
(при
стратегії В2).
Крім
цих рівнянь, добавимо рівняння, що
зв’язує частоти
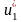 та
та
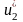 :
:
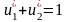 .
.
Розв’язуючи
отриману систему трьох рівнянь з трьома
невідомими знаходимо

Знайдемо
тепер оптимальну стратегію для гравця
В. Нехай стратегія для даного гравця
задається вектором
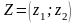 .
Тоді
.
Тоді
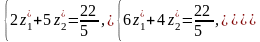
Розв’язуючи
цю систему рівнянь, матимемо
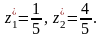 Отже, розв’язком гри є змішані стратегії
Отже, розв’язком гри є змішані стратегії
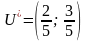 та
та
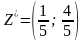 ,
а ціна гри
,
а ціна гри
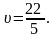
Дамо
тепер геометричну інтерпретацію
розв’язку даної гри. Для цього на
площині uOz
введемо систему координат й на осі Оu
відкладемо відрізок одиничної довжини
А1А2,
кожній точці якого поставимо у
відповідність деяку змішану стратегію
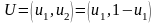 (мал. 8.4.1). Зокрема, точці
(мал. 8.4.1). Зокрема, точці
 відповідає стратегія
,
точці
відповідає стратегія
,
точці
 - стратегія
і т.д.
- стратегія
і т.д.
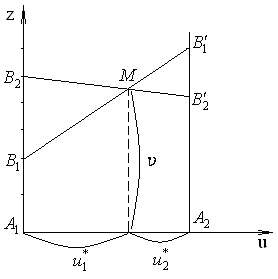
Мал. 8.4.1.
Через точки та проведемо перпендикуляри й на отриманих прямих будемо відкладати виграш гравців. На перпендикулярі, який співпадає з віссю Оz, відкладемо виграш гравця А при стратегії , а на другому – при стратегії . Якщо гравець А застосовує стратегію , то його виграш при стратегії гравця В дорівнює 2, а при стратегії він дорівнює 5. Числам 2 і 5 на осі Оz відповідають точки та .
Якщо
ж гравець А
приймає стратегію
,
то його виграш при стратегії
гравця В
дорівнює 6, а при стратегії
він дорівнює 4. Ці два числа визначають
дві точки
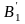 та
на перпендикулярі, проведеного через
точку
.
З’єднуючи між собою точки
та
,
та
та
на перпендикулярі, проведеного через
точку
.
З’єднуючи між собою точки
та
,
та
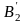 ,
матимемо дві прямі, відстань до яких
від осі Ou
визначає середній виграш при будь-якій
комбінації відповідних стратегій.
Наприклад, відстань від будь-якої точки
відрізка
до осі Оu
визначає середній виграш
,
матимемо дві прямі, відстань до яких
від осі Ou
визначає середній виграш при будь-якій
комбінації відповідних стратегій.
Наприклад, відстань від будь-якої точки
відрізка
до осі Оu
визначає середній виграш
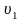 при будь-якій
комбінації стратегій
та
( з частотами
при будь-якій
комбінації стратегій
та
( з частотами
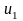 та
та
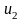 )
й стратегії
гравця В.
Ця відстань дорівнює
)
й стратегії
гравця В.
Ця відстань дорівнює
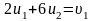 .
Аналогічно, середній виграш при
застосуванні стратегії
визначається ординатами точок, що
належать відрізку
.
.
Аналогічно, середній виграш при
застосуванні стратегії
визначається ординатами точок, що
належать відрізку
.
Таким
чином, ординати точок, що належать
ламаній
М
,
визначають мінімальний виграш гравця
А
при застосуванні ним будь-яких змішаних
стратегій. Ця мінімальна величина є
максимальною в точці М,
а отже, цій точці відповідає оптимальна
стратегія
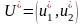 ,
а її ордината дорівнює ціні гри
.
Координати точки М
знаходимо як координати точки перетину
прямих
та
.
Тобто матимемо три рівняння:
,
а її ордината дорівнює ціні гри
.
Координати точки М
знаходимо як координати точки перетину
прямих
та
.
Тобто матимемо три рівняння:
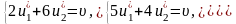
Розв’язавши
цю систему рівнянь, отримаємо:
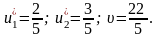
Аналогічно
знаходимо оптимальну стратегію для
гравця В.
Матимемо таку систему рівнянь:
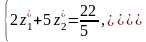
яка
має розв’язок:
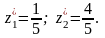
Отже,
розв’язком гри є змішані стратегії
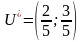 і
і
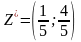 ,
а ціна гри
,
а ціна гри
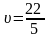 .
.
Підсумовуючи
викладене вище, можна вказати основні
етапи
знаходження розв’язку гри
 або
або
 :
:
1. Будують прямі, які відповідають стратегіям другого (першого) гравця.
2. Визначають нижню (верхню) границю виграшу.
3. Знаходять дві стратегії другого (першого) гравця, яким відповідають дві прямі, що перетинаються в точці з максимальною (мінімальною) ординатою.
4. Визначають ціну гри та оптимальні стратегії.
Зведення матричної гри до задачі лінійного програмування
Якщо
гра
або
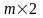 може бути розв’язана геометрично, то
у випадку гри
може бути розв’язана геометрично, то
у випадку гри
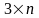
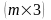 геометрична інтерпретація переходить
у простір, що ускладнює як її побудову,
так і сприйняття. У випадку ж, коли
геометрична інтерпретація переходить
у простір, що ускладнює як її побудову,
так і сприйняття. У випадку ж, коли
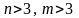 геометрична інтерпретація взагалі
неможлива.
Для розв'язування гри
геометрична інтерпретація взагалі
неможлива.
Для розв'язування гри
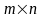 використовують
прийом зведення
її до задачі лінійного програмування.
використовують
прийом зведення
її до задачі лінійного програмування.
Нехай
розглядається парна гра зі стратегіями
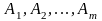 для
гравця
А та стратегіями
для
гравця
А та стратегіями
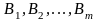 для
гравця В і платіжною матрицею
для
гравця В і платіжною матрицею
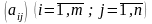 .
Необхідно
знайти оптимальні змішані
стратегії
і
,
де
.
Необхідно
знайти оптимальні змішані
стратегії
і
,
де
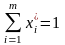 ,
,
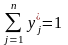 .
.
Знайдемо спочатку оптимальну стратегію гравця А. За основною теоремою теорії ігор така стратегія має забезпечити гравцеві виграш, не менший за ціну гри (поки що невідому величину) , за будь-якої поведінки гравця В.
Допустимо, що гравець А застосовує свою оптимальну стратегію, а гравець В - свою «чисту» -ту стратегію , тоді середній виграш гравця А дорівнюватиме:
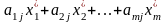 .
(8.5.1)
.
(8.5.1)
За
цих обставин виграш має бути не меншим,
ніж ціна гри. Отже,
для будь-якого значення
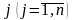 величина
виду (8.5.1) має
бути не меншою, ніж
:
величина
виду (8.5.1) має
бути не меншою, ніж
:
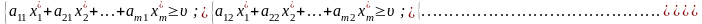
Розділивши всі обмеження на , отримаємо:
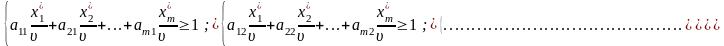
Позначивши
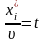 ,
маємо :
,
маємо :
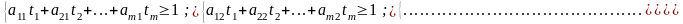 ,
,
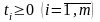 .
.
Враховуючи
умову, що
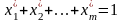 отримуємо
отримуємо
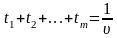 .
.
Необхідно зробити виграш максимальним. Цього можна досягти, коли вираз набуватиме мінімального значення. Отже, врешті маємо звичайну задачу лінійного програмування.
Цільова
функція:
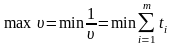 за умов
за умов
, .
Розв'язуючи
цю задачу симплексним методом, знаходимо
значення
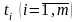 , а також величину
, а також величину
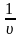 і значення
і значення
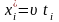 ,
що є оптимальним розв'язком початкової
задачі. Отже, визначено змішану
оптимальну стратегію
для
гравця А.
,
що є оптимальним розв'язком початкової
задачі. Отже, визначено змішану
оптимальну стратегію
для
гравця А.
За
аналогією можна записати задачу
лінійного програмування для визначення
оптимальної стратегії гравця В.
З
цією метою позначимо:
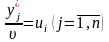 .
Маємо таку лінійну модель задачі:
.
Маємо таку лінійну модель задачі:
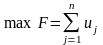 за умов
за умов
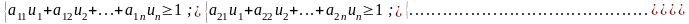 ,
,
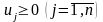 .
.
Очевидно, що задача лінійного програмування для гравця В є двоїстою до задачі гравця А, а тому оптимальний розв'язок однієї з них визначає також оптимальний розв'язок спряженої.
Задачі теорії ігор належать до задач прийняття рішень за умов невизначеності та ризику.
Невизначеність результатів гри зумовлена кількома чинниками. По-перше, як правило, кількість можливих варіантів розвитку подій дуже велика, тому передбачити результат гри неможливо. Простою ілюстрацією такого твердження є гра в шахи. Із-за безлічі можливих комбінацій знайти оптимальний розв'язок такої гри неможливо. По-друге, значний вплив на хід та результати гри мають випадкові чинники, дію яких передбачити неможливо, наприклад, у рулетці. По-третє, джерелом невизначеності є брак інформації щодо дій противника. Крім того, невизначеність певною мірою може стосуватися також і мети, якої прагне досягти суб'єкт. Не завжди таку мету можна виразити однозначно, а тим більше одним показником.
Зрозуміло, що коли початкові умови задачі містять значну кількість невизначених параметрів, то математичне дослідження не може дати чіткого обґрунтування раціонального розв'язку, однак і за відсутності повної визначеності кількісний аналіз дає наукову основу для прийняття рішень.
Задача 8.5.1. Знайти розв’язок гри, яка задається матрицею:
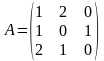 .
.
Розв’язання. Складемо двоїсту пару задач лінійного програмування:
пряма задача: знайти максимум функції
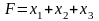 за умов
за умов

двоїста задача: знайти мінімум функції
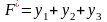 за умов
за умов
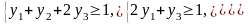
Знаходимо оптимальні плани прямої та двоїстої задач (табл. 8.5.1).
Таблиця 8.1.5.
і |
Базис |
Сб |
Р0 |
1 |
1 |
1 |
0 |
0 |
0 |
||||||||||||||||||
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
Р6 |
||||||||||||||||||||||
1 |
Р4 |
0 |
1 |
1 |
2 |
0 |
1 |
0 |
0 |
||||||||||||||||||
2 |
Р5 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
||||||||||||||||||
3 |
Р6 |
0 |
1 |
2 |
1 |
0 |
0 |
0 |
1 |
||||||||||||||||||
|
0 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
||||||||||||||||||||
1 |
Р4 |
0 |
1 |
1 |
2 |
0 |
1 |
0 |
0 |
||||||||||||||||||
2 |
Р3 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
||||||||||||||||||
3 |
Р6 |
0 |
1 |
2 |
1 |
0 |
0 |
0 |
1 |
||||||||||||||||||
|
1 |
0 |
-1 |
0 |
0 |
1 |
0 |
||||||||||||||||||||
1 |
Р2 |
1 |
|
|
1 |
0 |
|
0 |
0 |
||||||||||||||||||
2 |
Р3 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
||||||||||||||||||
3 |
Р6 |
0 |
|
|
0 |
0 |
- |
0 |
1 |
||||||||||||||||||
|
|
|
0 |
0 |
|
1 |
0 |
||||||||||||||||||||
З
даної таблиці видно, що вихідна задача
має оптимальний план
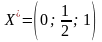 ,
а двоїста задача – оптимальний план
,
а двоїста задача – оптимальний план
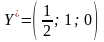 .
Отже ціна гри
.
Отже ціна гри
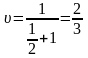 ,
а оптимальні стратегії гравців
,
а оптимальні стратегії гравців
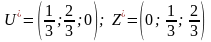 .
.
Підсумовуючи викладене вище, слід зазначити, що для всякої матричної гри можна записати симетричну пару двоїстих задач. Вірним є й обернене твердження: для будь-якої симетричної пари двоїстих задач можна записати матричну гру. Якщо кожна матрична гра має оптимальні стратегії, то не всяка задача лінійного програмування має розв’язок.
Отже, уможливлюючи розв'язування задач за умов невизначеності, навіть якщо неможливо знайти точний оптимальний розв'язок, математичні методи, в тому числі і методи теорії ігор, являють собою допоміжний матеріал, який дає змогу в складній ситуації оцінити кожен з можливих варіантів розвитку подій, а отже, прийняти виважене рішення.
33 Теорема про активні стратегії
Якщо
гравець
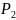 дотримується своєї оптимальної стратегії
дотримується своєї оптимальної стратегії
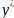 ,
то його середній виграш:
,
то його середній виграш:
F(x,
)=хС
залишається незмінним і рівним ціні
гри: V=F(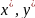 )
незалежно від гравця
)
незалежно від гравця
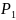 ,
,
якщо лише він не виходить за межі своїх активних стратегій.
Зауважимо: що твердження теореми про активні стратегії залишається вірним якщо поміняти місцями гравців і .
Ця теорема та її доведення дає можливість знайти в явному вигляді оптимальні змішані стратегії гравців і та ціну матричної гри 2х2.
Отже нехай платіжна матриця гри має вигляд:
С=
Зауважимо:
що
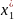 >0
і
>0
і
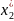 >0,
бо інакше матрична гра мала б сідлову
точку.
>0,
бо інакше матрична гра мала б сідлову
точку.
Напишемо наступні співвідношення:
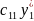 +
+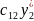 =V
=V
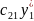 +
+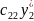 =V
=V
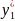 +
+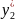 =1
=1
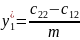 ;
;
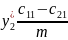 ;
V=
;
V=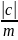 ;
;
m=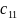 +
+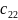 -
-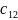 +
+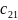
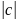 – визначник
матриці
С
– визначник
матриці
С
Аналогічно одержуємо оптимальну змішану стратегію гравця :
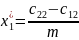 ;
;
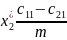
34.Загальна постановка задачі нелінійного програмування. Класифікація задач
Досить детально розглянута в розділах, присвячених лінійному програмуванню, задача пошуку оптимальних обсягів виробництва ґрунтується на допущеннях про лінійність зв’язку між витратами ресурсів і обсягами виготовленої продукції; між ціною, рекламою та попитом тощо. Але такі зв’язки насправді є нелінійними, тому точніші математичні моделі доцільно формулювати в термінах нелінійного програмування.
Нехай для деякої виробничої системи необхідно визначити план випуску продукції за умови найкращого способу використання її ресурсів. Відомі загальні запаси кожного ресурсу, норми витрат кожного ресурсу на одиницю продукції та ціни реалізації одиниці виготовленої продукції. Критерії оптимальності можуть бути різними, наприклад, максимізація виручки від реалізації продукції. Така умова подається лінійною залежністю загальної виручки від обсягів проданого товару та цін на одиницю продукції.
Однак, загальновідомим є факт, що за умов ринкової конкуренції питання реалізації продукції є досить складним. Обсяг збуту продукції визначається передусім її ціною, отже, як цільову функцію доцільно брати максимізацію не всієї виготовленої, а лише реалізованої продукції. Необхідно визначати також і оптимальний рівень ціни на одиницю продукції, за якої обсяг збуту був би максимальним. Для цього її потрібно ввести в задачу як невідому величину, а обмеження задачі мають враховувати зв’язки між ціною, рекламою та обсягами збуту продукції. Цільова функція в такому разі буде виражена добутком двох невідомих величин: оптимальної ціни одиниці продукції на оптимальний обсяг відповідного виду продукції, тобто буде нелінійною. Отже, маємо задачу нелінійного програмування.
Також добре відома транспортна задача стає нелінійною, якщо вартість перевезення одиниці товару залежить від загального обсягу перевезеного за маршрутом товару. Тобто коефіцієнти при невідомих у цільовій функції, що в лінійній моделі були сталими величинами, залежатимуть від значень невідомих (отже, самі стають невідомими), що знову приводить до нелінійності у функціоналі.
І нарешті, будь-яка задача стає нелінійною, якщо в математичній моделі необхідно враховувати умови невизначеності та ризик. Як показник ризику часто використовують дисперсію, тому для врахування обмеженості ризику потрібно вводити нелінійну функцію в систему обмежень, а мінімізація ризику певного процесу досягається дослідженням математичної моделі з нелінійною цільовою функцією.
Загальна
задача математичного програмування
формулюється так: знайти такі значення
змінних xj ![]() ,
щоб цільова функція набувала екстремального
(максимального чи мінімального) значення:
,
щоб цільова функція набувала екстремального
(максимального чи мінімального) значення:
![]() (8.1)
(8.1)
за умов:
![]() (
(![]() );
(8.2)
);
(8.2)
![]() .
(8.3)
.
(8.3)
Якщо
всі функції ![]() та
та ![]() ,
є
лінійними, то це задача лінійного
програмування, інакше (якщо хоча б одна
з функцій є нелінійною) маємо задачу
нелінійного програмування.
,
є
лінійними, то це задача лінійного
програмування, інакше (якщо хоча б одна
з функцій є нелінійною) маємо задачу
нелінійного програмування.
35. Геометрична інтерпретація задачі нелінійного програмування
Геометрично
цільова функція (8.1) визначає деяку
поверхню, а обмеження (8.2)—(8.3) — допустиму
підмножину n-вимірного
евклідового простору. Знаходження
оптимального розв’язку задачі
нелінійного програмування зводиться
до відшукання точки з допустимої
підмножини, в якій досягається поверхня
найвищого (найнижчого) рівня.
Якщо
цільова функція неперервна, а допустима
множина розв’язків замкнена, непуста
і обмежена, то глобальний максимум
(мінімум) задачі існує.
Найпростішими
для розв’язування є задачі нелінійного
програмування, що містять систему
лінійних обмежень та нелінійну цільову
функцію. В цьому разі область допустимих
розв’язків є опуклою, непустою,
замкненою, тобто обмеженою.
Розглянемо
приклад геометричного способу
розв’язування задачі нелінійного
програмування.
Зн![]() айти
мінімальне і максимальне значення
функції:
айти
мінімальне і максимальне значення
функції:
![]() за
умов:
за
умов:
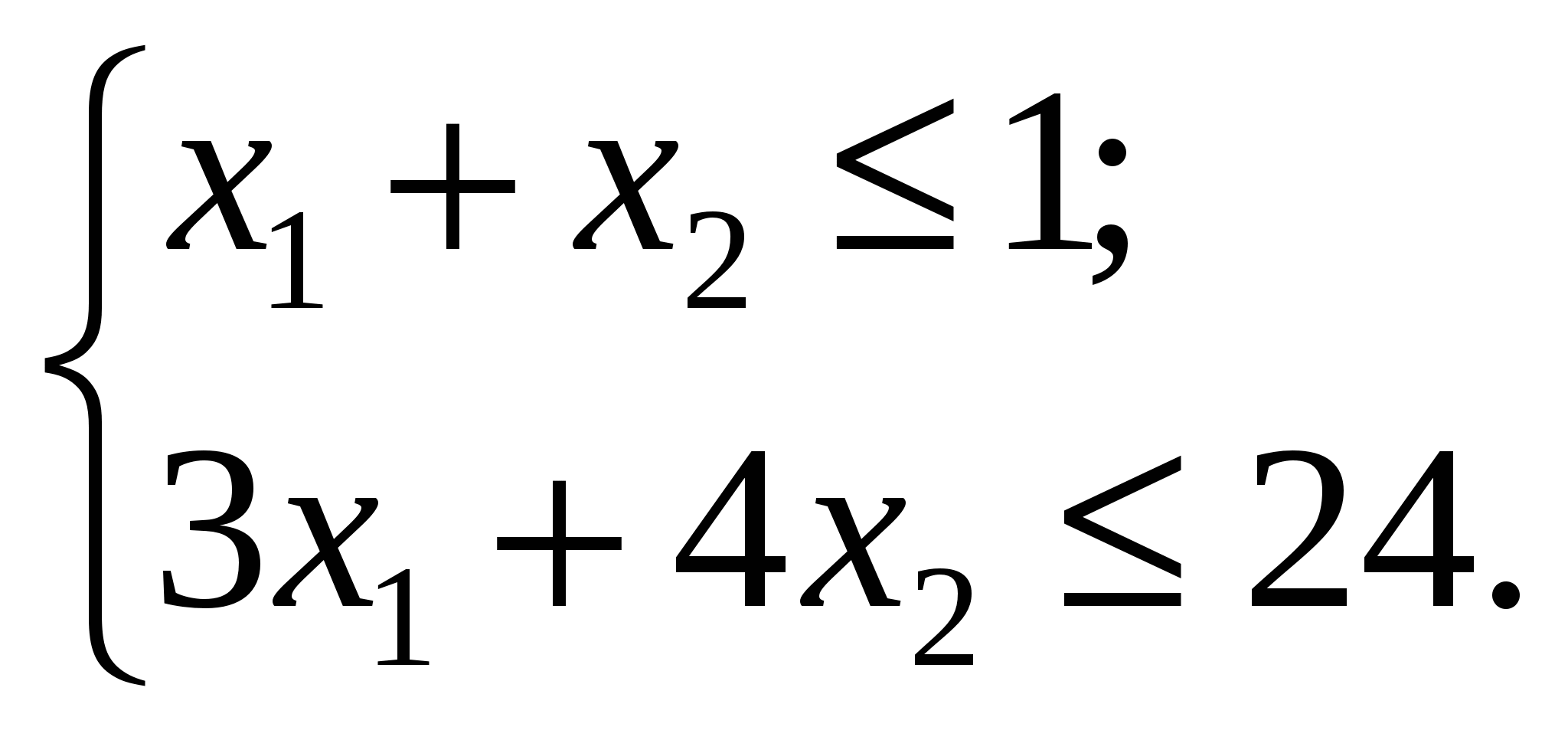
Рис.
8.1
![]() .
Розв’язання.
Область допустимих розв’язків утворює
чотирикутник АВСD (рис.
8.1). Геометрично цільова функція
являє собою коло з центром у точці М (2; 2),
квадрат радіуса якого
.
Розв’язання.
Область допустимих розв’язків утворює
чотирикутник АВСD (рис.
8.1). Геометрично цільова функція
являє собою коло з центром у точці М (2; 2),
квадрат радіуса якого ![]() .
Це означає, що її значення буде
збільшуватися (зменшуватися) зі
збільшенням (зменшенням) радіуса кола.
Проведемо з точки М кола
різних радіусів. Функція Z має
два локальних максимуми: точки В (0; 6)
і С (8; 0).
Обчислимо значення функціонала в цих
точках:
.
Це означає, що її значення буде
збільшуватися (зменшуватися) зі
збільшенням (зменшенням) радіуса кола.
Проведемо з точки М кола
різних радіусів. Функція Z має
два локальних максимуми: точки В (0; 6)
і С (8; 0).
Обчислимо значення функціонала в цих
точках:
![]() ,
,
![]() .
Оскільки
.
Оскільки ![]() ,
то точка С (8; 0)
є точкою глобального максимуму.
Очевидно,
що найменший радіус
,
то точка С (8; 0)
є точкою глобального максимуму.
Очевидно,
що найменший радіус ![]() ,
тоді:
,
тоді:
![]() .
Тобто точка М є
точкою мінімуму, оскільки їй відповідає
найменше можливе значення цільової
функції.
Зазначимо,
що в даному разі точка, яка відповідає
оптимальному плану задачі (мінімальному
значенню функціонала), знаходиться
всередині багатокутника допустимих
розв’язків, що в задачах лінійного
програмування неможливо.
Зн
.
Тобто точка М є
точкою мінімуму, оскільки їй відповідає
найменше можливе значення цільової
функції.
Зазначимо,
що в даному разі точка, яка відповідає
оптимальному плану задачі (мінімальному
значенню функціонала), знаходиться
всередині багатокутника допустимих
розв’язків, що в задачах лінійного
програмування неможливо.
Зн![]() айти
мінімальне значення функції:
айти
мінімальне значення функції:
![]() за
умов:
за
умов:
![]() .
Розв’язування.
У даному прикладі множина допустимих
розв’язків складається з двох окремих
частин, необмежених зверху (рис.
8.2). Цільова функція аналогічно
попередньому випадку є колом з центром
у точці М (4; 4).
Функція Z має
два локальних мінімуми: в точці А (
.
Розв’язування.
У даному прикладі множина допустимих
розв’язків складається з двох окремих
частин, необмежених зверху (рис.
8.2). Цільова функція аналогічно
попередньому випадку є колом з центром
у точці М (4; 4).
Функція Z має
два локальних мінімуми: в точці А (![]() ),
і в точці В (
),
і в точці В (![]() ).
З
).
З
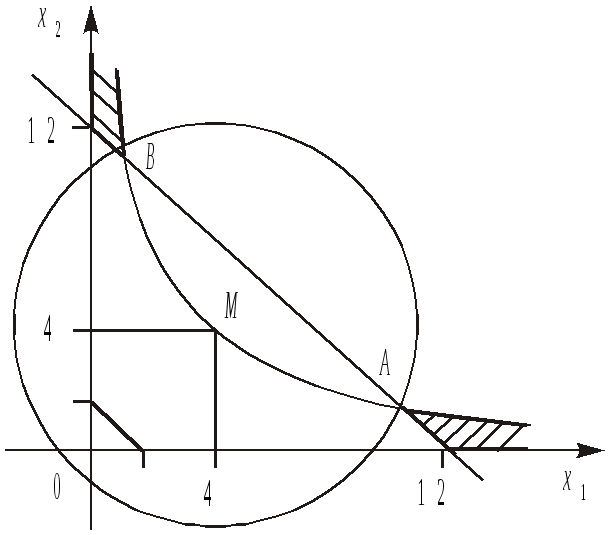 Рис.
8.2.
начення функціонала в цих
точках однакове і дорівнює:
Рис.
8.2.
начення функціонала в цих
точках однакове і дорівнює:
![]() .
Отже,
маємо два альтернативні оптимальні
плани.
Даний
приклад ілюструє ще одну особливість
задач нелінійного програмування: на
відміну від задач лінійного
програмування багатогранник допустимих
розв’язків задачі нелінійного
програмування не обов’язково буде
опуклою множиною.
.
Отже,
маємо два альтернативні оптимальні
плани.
Даний
приклад ілюструє ще одну особливість
задач нелінійного програмування: на
відміну від задач лінійного
програмування багатогранник допустимих
розв’язків задачі нелінійного
програмування не обов’язково буде
опуклою множиною.
36.Метод множників Лагранжа
Ідея методу множників Лагранжа полягає в заміні початкової задачі простішою. Для цього цільову функцію замінюють іншою, з більшою кількістю змінних, тобто такою, яка включає в себе умови, що подані як обмеження. Після такого перетворення дальше розв’язування задачі полягає в знаходженні екстремуму нової функції, на змінні якої не накладено ніяких обмежень. Тобто від початкової задачі пошуку умовного екстремуму переходимо до задачі відшукання безумовного екстремального значення іншої функції. Отже, завдяки такому перетворенню можливе застосування методів класичного знаходження екстремуму функції кількох змінних.
У попередньому параграфі наведена необхідна умова існування локального екстремуму неперервної та диференційовної функції двох змінних.
Узагальнення необхідної умови існування локального екстремуму функції n змінних має аналогічний вигляд. Отже, для розв’язування задачі необхідно знайти вирази частинних похідних нової цільової функції за кожною змінною і прирівняти їх до нуля. В результаті отримаємо систему рівнянь. Її розв’язок визначає так звані стаціонарні точки, серед яких є і шукані екстремальні значення функції.
Розглянемо метод множників Лагранжа для розв’язування задачі нелінійного програмування, що має вигляд:
![]() (8.6)
(8.6)
за умов:
![]() ,
(8.7)
,
(8.7)
де
функції ![]() і
і ![]() мають
бути диференційовними.
мають
бути диференційовними.
Задача
(8.6), (8.7) полягає в знаходженні екстремуму
функції ![]() за
умов виконання обмежень
за
умов виконання обмежень ![]() .
.
Переходимо до задачі пошуку безумовного екстремуму. В літературі [13, 28] теоретично доведено, що постановки та розв’язання таких задач еквівалентні.
Замінюємо цільову функцію (8.6) на складнішу. Ця функція називається функцією Лагранжа і має такий вигляд:
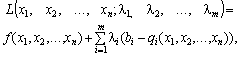 (8.8)
(8.8)
де ![]() —
деякі невідомі величини, що
називаються множниками
Лагранжа.
—
деякі невідомі величини, що
називаються множниками
Лагранжа.
Знайдемо частинні похідні і прирівняємо їх до нуля:
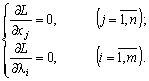
![]() (8.9)
(8.9)
Друга група рівнянь системи (8.9) забезпечує виконання умов (8.7) початкової задачі нелінійного програмування.
Система (8.9), як правило, нелінійна.
Розв’язками
її є ![]() і
і ![]() —
стаціонарні точки. Оскільки, ці розв’язки
отримані з необхідної умови екстремуму,
то вони визначають максимум, мінімум
задачі (8.6), (8.7) або можуть бути точками
перегину (сідловими точками).
—
стаціонарні точки. Оскільки, ці розв’язки
отримані з необхідної умови екстремуму,
то вони визначають максимум, мінімум
задачі (8.6), (8.7) або можуть бути точками
перегину (сідловими точками).
Для
діагностування стаціонарних точок і
визначення типу екстремуму необхідно
перевірити виконання достатніх умов
екстремуму, тобто дослідити в околі
стаціонарних точок диференціали другого
порядку (якщо для функцій ![]() існують
другі частинні похідні і вони неперервні).
існують
другі частинні похідні і вони неперервні).
Узагальнення
достатньої умови існування локального
екстремуму для функції n змінних
приводить до такого правила: за функцією
Лагранжа виду (8.8) будується матриця
Гессе, що має блочну структуру
розмірністю ![]() :
:
![]()
де
О — матриця розмірністю ![]() ,
що складається з нульових елементів,
,
що складається з нульових елементів,
Р
— матриця розмірністю ![]() ,
елементи якої визначаються так:
,
елементи якої визначаються так:
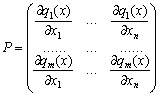 ,
,
![]() —
транспонована
матриця до Р розмірністю
—
транспонована
матриця до Р розмірністю ![]() ,
,
Q —
матриця розмірністю ![]() виду:
виду:
![]() ,
де
,
де ![]() .
.
Розглянемо ознаки виду екстремуму розв’язку системи (8.9). Нехай стаціонарна точка має координати і .
1.
Точка ![]() є
точкою максимуму, якщо, починаючи з
головного мінору порядку (m +
1), наступні (n – m)
головних мінорів матриці Н утворюють
знакозмінний числовий ряд, знак першого
члена якого визначається множником
є
точкою максимуму, якщо, починаючи з
головного мінору порядку (m +
1), наступні (n – m)
головних мінорів матриці Н утворюють
знакозмінний числовий ряд, знак першого
члена якого визначається множником ![]() .
.
2.
Точка
є
точкою мінімуму, якщо, починаючи з
головного мінору порядку (m +
1), знак наступних (n – m)
головних мінорів матриці Н визначається
множником ![]() .
.
37.Узагальнення методу множників Лагранжа. Теорема Куна-Таккера. Теорема Куна—Таккера
Розглянутий метод множників Лагранжа уможливлює знаходження лише локальних сідлових точок функції Лагранжа.
Теорема Куна—Таккера дає змогу встановити типи задач, для яких на множині допустимих розв’язків існує лише один глобальний екстремум зумовленого типу. Вона тісно пов’язана з необхідними та достатніми умовами існування сідлової точки.
Розглянемо задачу нелінійного програмування, яку, не зменшуючи загальності, подамо у вигляді:
![]() ,
(8.22)
,
(8.22)
![]() ,
(8.23)
,
(8.23)
![]() .
(8.24)
.
(8.24)
(Очевидно, що знак нерівності можна змінити на протилежний множенням лівої і правої частин обмеження на (– 1)).
Теорема
8.1. (Теорема Куна—Таккера). Вектор Х* є
оптимальним розв’язком задачі
(8.22)—(8.24) тоді і тільки тоді, коли існує
такий вектор ![]() ,
що при
,
що при ![]() для
всіх
для
всіх ![]() точка
точка ![]() є
сідловою точкою функції Лагранжа
є
сідловою точкою функції Лагранжа
![]() ,
,
і
функція мети ![]() для
всіх
для
всіх ![]() угнута,
а функції
угнута,
а функції ![]() —
опуклі.
—
опуклі.
Доведення. Необхідність. Нехай Х* — оптимальний план задачі (8.22)—(8.24), тобто є точкою глобального максимуму задачі. Отже, для всіх інших планів задачі Х з множини допустимих розв’язків виконуватиметься співвідношення:
![]() .
.
Розглянемо
тепер вектор ![]() ,
що відповідає точці глобального
максимуму
,
що відповідає точці глобального
максимуму ![]() ,
і значення функції Лагранжа в
точках
,
і значення функції Лагранжа в
точках ![]() ,
, ![]() ,
, ![]() ,
де
—
довільний план задачі з множини допустимих
розв’язків,
,
де
—
довільний план задачі з множини допустимих
розв’язків, ![]() —
вектор множників Лагранжа, що відповідає Х.
—
вектор множників Лагранжа, що відповідає Х.
З
умови (8.21) маємо: ![]() ,
тоді
,
тоді
![]() .
(8.25)
.
(8.25)
Для
точки з координатами
деякі
доданки виду ![]() можуть
бути відмінними від нуля. Оскільки за
умовою задачі
можуть
бути відмінними від нуля. Оскільки за
умовою задачі ![]() ,
то лише за умови, що
,
матимемо нерівність:
,
то лише за умови, що
,
матимемо нерівність:
![]() .
.
Функція ![]() —
лінійна відносно
—
лінійна відносно ![]() ,
тобто остання нерівність виконується
для будь-якого
.
Отже, точка
,
тобто остання нерівність виконується
для будь-якого
.
Отже, точка ![]() —
точка глобального мінімуму по
функції
Лагранжа.
—
точка глобального мінімуму по
функції
Лагранжа.
Для
встановлення нерівності, що відповідає
лівій частині умови (8.13), а саме: ![]() ,
скористаємося також рівнянням (8.21),
підсумувавши його по і:
,
скористаємося також рівнянням (8.21),
підсумувавши його по і: ![]() .
За умовою теореми
.
За умовою теореми ![]() —
угнуті функції і
,
тому виконується таке рівняння:
—
угнуті функції і
,
тому виконується таке рівняння:

Отже, у точці Х* функція Лагранжа має глобальний максимум по Х, що повністю доводить необхідність теореми.
Достатність.
Для доведення достатності умов теореми
потрібно виходити з того, що ![]() ,
, ![]() —
сідлова точка функції
—
сідлова точка функції ![]() (тобто
для
виконується
нерівність (8.13)), і необхідно довести,
що тоді Х*
є оптимальним планом задачі опуклого
програмування.
(тобто
для
виконується
нерівність (8.13)), і необхідно довести,
що тоді Х*
є оптимальним планом задачі опуклого
програмування.
Підставимо у нерівність (8.13) вираз функції Лагранжа (8.12) для задачі (8.22)—(8.23):
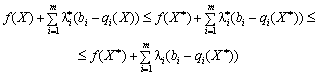 (8.26)
(8.26)
при
всіх значеннях ![]() .
.
Розглянемо праву частину подвійної нерівності (8.26).
![]()
![]()
![]()
![]() .
.
Остання
нерівність має виконуватися для всіх
.
Крім того, ![]() ,
тобто нерівність справджується лише у
разі, коли
,
тобто нерівність справджується лише у
разі, коли
![]() .
.
Тоді з лівої частини нерівності (8.26) маємо:
![]()
![]() .
.
Через
те що ![]() ,
приходимо до нерівності
,
приходимо до нерівності ![]() ,
яка справджується для всіх значень
.
,
яка справджується для всіх значень
.
Отже, точка Х* задовольняє обмеження і надає максимального значення цільовій функції задачі, тому що для всіх інших функція набуває менших значень, ніж у точці Х*, тобто вона є оптимальним планом задачі нелінійного програмування. Достатність умов тереми доведено.
Умови теореми Куна — Таккера виконуються лише для задач, що містять опуклі функції.
38.Градієнтні методи безумовної оптимізації
1.2.1 Загальна схема градієнтного спускуЯк відомо, градієнт функції в деякій точці xk спрямований в бік найшвидшого локального зростання функції й перпендикулярний лінії рівня (поверхня постійного значення функції f (x), що проходить через точку xk). Вектор, протилежний градієнту , називається антиградієнтом, що спрямований убік найшвидшого убування функції f (x). Вибираючи як напрямок спуска pk антиградієнт - у точці xk, ми приходимо до ітераційного процесу виду:
xk+1 = xk - k f' (xk), k>0, k=0, 1, 2, …
У координатній формі цей процес записується в такий спосіб:
Всі ітераційні процеси, у яких напрямок руху на кожному кроці збігається з антиградієнтом функції, називаються градієнтними методами. Вони відрізняються друг від друга тільки способом вибору кроку k. Існує багато різних способів вибору k, але найпоширеніші: метод з постійним кроком, метод із дробленням кроку й метод найшвидшого спуска.
1.2.4 Метод найшвидшого спуска
У градієнтному методі з постійним кроком величина кроку, що забезпечує убування функції f (x) від ітерації до ітерації, виявляється дуже малої, що приводить до необхідності проводити велику кількість ітерації для досягнення точки мінімуму. Тому методи спуска зі змінним кроком є більше ощадливими. Алгоритм, на кожній ітерації якого крок до вибирається з умови мінімуму функції f (x) у напрямку руху, тобто:
називається методом найшвидшого спуска. Зрозуміло, цей спосіб вибору до складніше раніше розглянутих варіантів.
Реалізація методу найшвидшого спуска припускає рішення на кожній ітерації досить трудомісткої допоміжної задачі одномірної мінімізації. Як правило, метод найшвидшого спуска, проте, дає виграш у числі машинних операцій, оскільки забезпечує рух із самим вигідним кроком, тому що рішення задачі одномірної мінімізації пов'язане з додатковими обчисленнями тільки самої функції f (x), тоді як основний машинний час витрачається на обчислення її градієнта .
Варто мати на увазі, що одномірну мінімізацію можна робити будь-яким методом одномірної оптимізації, що породжує різні варіанти методу найшвидшого спуска.
Схема алгоритму
Крок 1.
Задаються х0, 3. Обчислюється градієнт , напрямок пошуку.
Привласнюється до=0.
Крок 2.
Визначається точка чергового експерименту:
хк+1 = хк - до,
де до - мінімум задачі одномірної мінімізації:
Крок 3.
Обчислюється значення градієнта в точці хк+1: .
Крок 4.
Якщо ||||3, то пошук точки мінімуму закінчується й покладається:
Інакше до=до+1 і перехід до кроку 2.

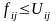 ,
,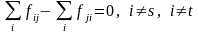 ,
,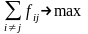 ,
,