
- •1.Опуклі множини та їх властивості
- •2.Загальна злп та її допустима область
- •3.Графічний метод розв’язування задач лінійного програмування
- •4. Загальна економіко-математична модел задачі лінійного програмування
- •5. Алгоритм симплекс методу
- •Скiнченнiсть симплекс-методу
- •Симплекс-таблицi
- •7. Метод штучного базису
- •Зв’язок міжрозв’язками пари двоїстихзадач.Теорема двоїстості
- •12.Муравйов
- •13.Олішевський
- •14.Методи знаходження початкового базисного розвязку тзлп
- •1. Метод пiвнiчно-захiдного кута
- •2. Метод мінімального елемента
- •17.Рудик
- •18.Рудик
- •19.Аракелова
- •24. Метод відтинання. Алгоритм Гоморі
- •25. Частково цiлочисельнi задачі лінійного програмування. Другий метод Гоморi
- •26. Третiй метод Гоморi
- •Алгоритм третього методу Гоморi
- •5. Знаходимо індекс l з умови: де мінімум визначається на
- •27.Стельмах
- •28.Стельмах
- •Задачі теорії гри
- •Основні поняття теорії ігор
- •Матричні ігри двох осіб
- •Гра зі змішаними стратегіями
- •Геометрична інтерпретація гри теорії гри
- •Зведення матричної гри до задачі лінійного програмування
- •33 Теорема про активні стратегії
- •34.Загальна постановка задачі нелінійного програмування. Класифікація задач
- •35. Геометрична інтерпретація задачі нелінійного програмування
- •36.Метод множників Лагранжа
- •37.Узагальнення методу множників Лагранжа. Теорема Куна-Таккера. Теорема Куна—Таккера
- •38.Градієнтні методи безумовної оптимізації
5. Алгоритм симплекс методу
Визначення початкового опорного плану задачі лінійного програмування.
Побудова симплексної таблиці.
Перевірка опорного плану на оптимальність за допомогою оцінок
 .
Якщо всі оцінки задовольняють умову
оптимальності, то визначений опорний
план є оптимальним планом задачі. Якщо
ж хоча б одна з оцінок не задовольняє
умову оптимальності, то переходимо до
нового плану або ж встановлюємо, що
оптимального плану нема.
.
Якщо всі оцінки задовольняють умову
оптимальності, то визначений опорний
план є оптимальним планом задачі. Якщо
ж хоча б одна з оцінок не задовольняє
умову оптимальності, то переходимо до
нового плану або ж встановлюємо, що
оптимального плану нема.Перехід до нового опорного плану задачі здійснюється визначенням розв’язувального елемента та розрахунку елементів нової симплекс таблиці.
Повторення дій, починаючи з пункту (3).
У разі застосування симплекс методу до розв’язування задач лінійного програмування можливі такі випадки:
Якщо в оцінковому рядку останньої симплекс таблиці =0 відповідає вільній (небазисній) змінній, то це означає, що задача лінійного програмування має альтернативний оптимальний план. Отримати його можна, вибравши розв’язувальний елемент у зазначеному стовпці таблиці та здійснивши 1 крок симплекс методу.
Якщо при переході у симплекс метод від одного опорного плану задачі до іншого, в напрямному стовпчику немає додатних елементів
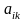 ,
тобто неможливо вибрати змінну, яка
має бути виключена з базису, то це
означає, що цільова функція задачі є
необмеженою і оптимальних планів не
існує.
,
тобто неможливо вибрати змінну, яка
має бути виключена з базису, то це
означає, що цільова функція задачі є
необмеженою і оптимальних планів не
існує.Якщо для опорного плану задачі оцінки задовольняють умову оптимальності, але при цьому хоча б одна штучна змінна є базисною і має додатне значення, то це означає, що система обмежень задачі несумісна й оптимальних планів такої задачі не існує.
Скiнченнiсть симплекс-методу
ЗЛП
будемо називати невиродженою, якщо
невиродженими є всі її базисні розв'язки.
Розглянемо
спочатку невироджену ЗЛП. Якщо вона
записана у канонічній
формі
![]()
то
це означає, що величини
![]() строго додатні. При цьому додатною є
також величина
строго додатні. При цьому додатною є
також величина
![]()
Оскiльки
значення цільової функції у двох
послідовних iтерацiйних
точках
![]() та
та
![]() пов'язані співвідношенням
пов'язані співвідношенням
![]()
причому
![]() Звiдси,
приймаючи до уваги, що число
вершин
допустимої множини скiнченне, приходимо
до висновку про скінченність
симплексного
методу.
Звiдси,
приймаючи до уваги, що число
вершин
допустимої множини скiнченне, приходимо
до висновку про скінченність
симплексного
методу.
У
випадку виродженої ЗЛП одна або декілька
базисних змінних базисного
розв'язку
можуть бути рівними нулю. При цьому
![]() i, отже,
i, отже,
![]()
Це
може привести до того, що на протязі
ряду iтерацiй симплекс-методу буде
розглядатися одна i та ж вершина, а
змінюватимуться лише базисні вектори,
що відповідають нульовим базисним
змінним i можливе повернення до початкового
базису, що відповідає цій вершині. Таке
явище називається за циклюванням
симплексного методу. Можливiсть
зациклювання є реальною лише тоді, коли
для розглядуваного базисного розв'язку
принаймні дві базисні змінні дорівнюють
нулю. У цьому випадку існує неоднозначність
при виборі вектора, що підлягає виведенню
з базисних при
![]() Така ж неоднозначність може мати місце
i для невиродженого базисного розв'язку.
Однак у цьому випадку
Така ж неоднозначність може мати місце
i для невиродженого базисного розв'язку.
Однак у цьому випадку
![]() i новий базисний розв'язок приводить до
зменшення значення цільової функції.
При цьому, внаслідок згаданої
неоднозначності, новий базисний
розв'язок буде виродженим.
i новий базисний розв'язок приводить до
зменшення значення цільової функції.
При цьому, внаслідок згаданої
неоднозначності, новий базисний
розв'язок буде виродженим.
Незважаючи на те, що при розв'язуванні практичних задач зациклювання симплекс-методу не зустрічалося i що побудовано лише декілька штучних прикладів, де це явище має місце, розроблені різні методи його попередження (виходу з циклу). Зроблені вище зауваження свідчать про те, що будь-який з цих методів має гарантувати однозначність вибору вектора, що підлягає виведенню з базисних.
