Билет 27

1.Построение хода лучей в бипризме Френеля.

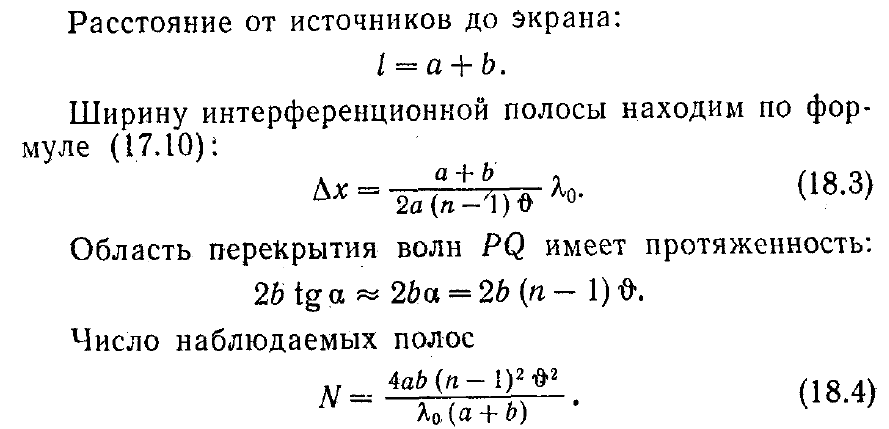
2.Уровни энергии

Уровни энергии

Для получения энергетических уровней в атоме водорода в рамках модели Бора записывается второй закон Ньютона для движения электрона по круговой орбите в поле кулоновской силы притяжения:

где m — масса электрона, e — его заряд, Z — заряд ядра и k — кулоновская константа, зависящая от выбора системы единиц. Это соотношение позволяет выразить скорость электрона через радиус его орбиты:

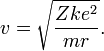
Энергия электрона равна сумме кинетической энергии движения и его потенциальной энергии:

Используя правило квантования Бора, можно записать:

откуда радиус орбиты выражается через квантовое число n. Подстановка радиуса в выражение для энергии даёт:

Комбинация констант

 ≈ 13,6 эВ

называется постоянной Ридберга. Она равна энергии связи электрона в атоме водорода в основном состоянии, т.е. минимальной энергии, необходимой для ионизации атома водорода в низшем (стабильном) энергетическом состоянии

3.Закон Гука

Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Он имеет вид простой пропорциональности.

В словесной форме закон звучит следующим образом:

Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации

Для тонкого растяжимого стержня закон Гука имеет вид:

Здесь   — сила, которой растягивают (сжимают) стержень,   — абсолютное удлинение (сжатие) стержня, а   — коэффициент упругости (или жёсткости).

Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения   и длины  ) явно, записав коэффициент упругости как

Величина   называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.

Если ввести относительное удлинение

и нормальное напряжение в поперечном сечении

то закон Гука в относительных единицах запишется как

В такой форме он справедлив для любых малых объёмов материала.

Также при расчёте прямых стержней применяют запись закона Гука в относительной форме

Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

Энергия упругой деформации

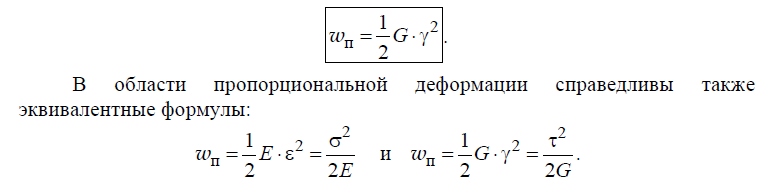
Билет 28

1. Спектральные закономерности атома водорода и их объяснения в теории Бора.

Серия	Частота излучения	Диапазон волн
Лаймана	ω =R(1/12-1/n2) n=2,3,4…	Ультрафиолет УФ
Бальмера	ω =R(1/22-1/n2) n=3,4,5…	Видимая область и ближний УФ
Пашена	ω =R(1/32-1/n2) n=4,5,6…	Инфракрасный диапазон ИК
Брэкета	ω =R(1/42-1/n2) n=5,6,7…
Пфунда	ω =R(1/52-1/n2) n=6,7,8…

R=2.07*10¹⁶ c^-1 Постоянная Ридберга.

Теория атома водорода по Бору

Движение электрона в кулоновском поле ядра с зарядом Ze :

F/m_e=F_цс/m_e=v²/r, F/m_e=F_кул/m_e=Ze²/r²/me→v²=Ze²/m_er

С другой стороны по 3 правилу Бора:

L= m_evr=nћ→v=nћ/m_er

(nћ/ m_er)²=Ze²/ m_er, r=r_n=ћ²n²/ Ze² m_er, (n=1,2,3,…)

2. Барометрическая формула. Распределение Больцмана.

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.

Для идеального газа, имеющего постоянную температуру   и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения   одинаково), барометрическая формула имеет следующий вид:

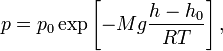
где   — давление газа в слое, расположенном на высоте  ,   — давление на нулевом уровне ( ),   — молярная масса газа,   — газовая постоянная,   — абсолютная температура. Из барометрической формулы следует, что концентрация молекул   (или плотность газа) убывает с высотой по тому же закону:

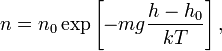
где   — масса молекулы газа,   — постоянная Больцмана.

3.Внутренная энергия идеального газа.

В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Средняя энергия движения одной молекулы равна

Так как в одном киломоле содержится   молекул, то внутренняя энергия одного киломоля газа будет

Учитывая, что   , получим

Для любой массы m газа, т.е. для любого числа киломолей   внутренняя энергия

Из этого выражения следует, что внутренняя энергия является однозначной функцией состояния и, следовательно, при совершении системой любого процесса, в результате которого система возвращается в исходное состояние, полное изменение внутренней энергии равно нулю. Математически это записывается в виде тождества