Билет 22
Билет 22
1.Упругие свойства твердых тел. Типы деформации. Закон Гука.
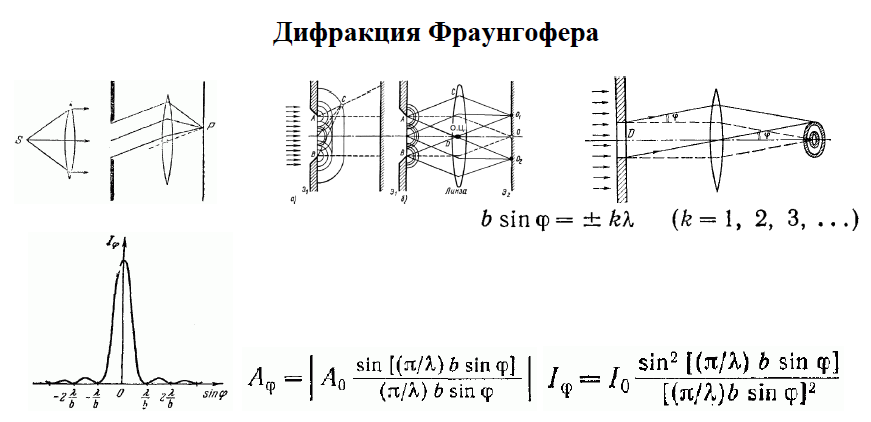
2.Дифракция Фраунгофера на 1 щели.
3.Основные уравнения молекулярно-кинетической теории.
1. УПРУГИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
Изменение размеров и формы тел называется деформацией. Деформация происходит под действием сил. Если после прекращения действия сил, вызвавших деформацию, тело принимает первоначальные размеры и форму, деформация называется упругой. Упругие деформации происходят в том случае, если сила, обусловившая деформацию, не превосходит некоторый, определенный для каждого конкретного тела предел. При превышении этого предела тело получает остаточные (пластические) деформации, т.е. такие деформации, которые сохраняются и после прекращения действия силы. Все возможные виды упругих деформаций твердого тела могут быть сведены к двум основным: растяжению-сжатию и сдвигу.
Типы деформации:
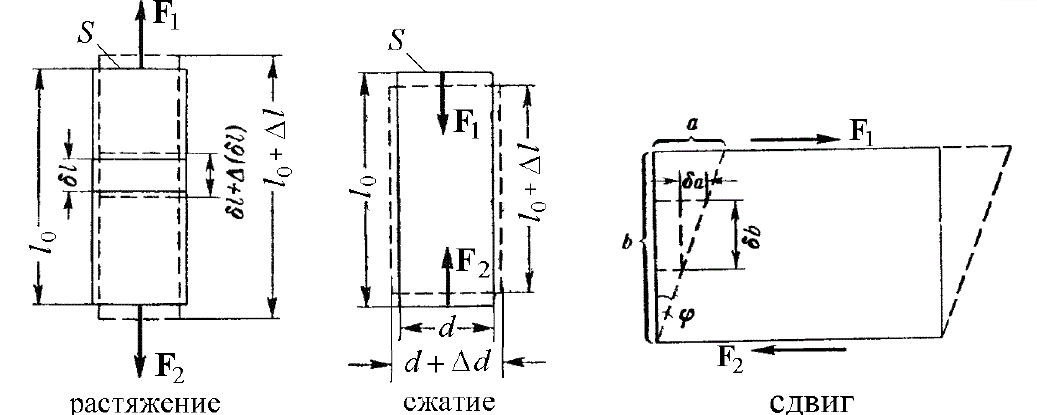
Рис. 45 Рис. 46 Рис. 47
φ= (2l/πR4G)*M
где l – длина стержня, R – радиус его сечения, G – модуль сдвига, М – вращательный момент (момент сил).
Закон Гука для стержней из однородного материала – относительное удлинение при упругой деформации пропорционально силе, приходящейся на единицу площади поперечного сечения стержня:
2.
3.
,
где k является постоянной
Больцмана (отношение универсальной
газовой постоянной R к числу
Авогадро NA), i —
число степеней свободы молекул (
в
большинстве задач про идеальные газы,
где молекулы предполагаются сферами
малого радиуса, физическим аналогом
которых могут служить инертные газы),
а T -
абсолютная температура.
Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) газовой системы с микроскопическими (масса молекул, средняя скорость их движения).
Вывод основного уравнения МКТ
Пусть
имеется кубический сосуд с ребром
длиной 
и
одна частица массой 
в
нём.
Обозначим
скорость движения 
,
тогда перед столкновением со стенкой
сосуда импульс частицы
равен 
,
а после — 
,
поэтому стенке передается импульс 
.
Время, через которое частица сталкивается
с одной и той же стенкой, равно 
.
Отсюда следует:
Так
как давление 
,
следовательно сила 
Подставив,
получим: 
П
реобразовав: 
Так
как рассматривается кубический сосуд,
то 
Отсюда:
.
Соответственно, 
и 
.
Таким
образом, для большого числа частиц
верно следующее: 
,
аналогично для осей y и z.
Поскольку 
,
то 
.
Это следует из того, что все направления
движения молекул в
хаотичной среде равновероятны.
Отсюда 
или 
.
Пусть 
—
среднее значение кинетической энергии
всех молекул, тогда:
,
откуда, используя то, что 
,
а 
,
имеем 
.
Билет 23
1.Энергия упругой деформации. Диаграмма растяжений.
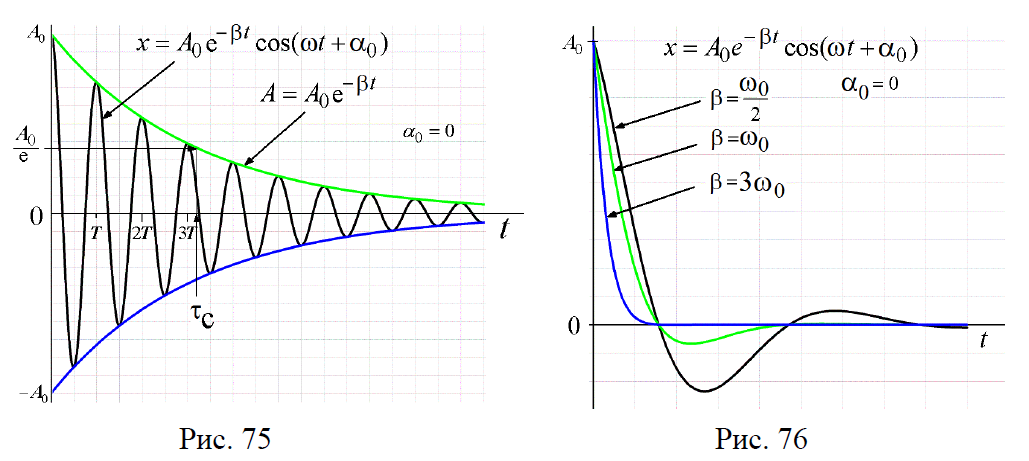
2.Затухающие колебания. Уравнение и решение. Декремент затухания. Добротность.
3.Строение атомного ядра. Состав ядра. Размеры ядер. Заряд, масса, спин ядра.
1.Изменение размеров и формы тел называется деформацией. Деформация происходит под действием сил. Если после прекращения действия сил, вызвавших деформацию, тело принимает первоначальные размеры и форму, деформация называется упругой. Упругие деформации происходят в том случае, если сила, обусловившая деформацию, не превосходит некоторый, определенный для каждого конкретного тела предел. При превышении этого предела тело получает остаточные (пластические) деформации, т.е. такие деформации, которые сохраняются и после прекращения действия силы. Все возможные виды упругих деформаций твердого тела могут быть сведены к двум основным: растяжению-сжатию и сдвигу.
Диаграмма деформации. Качественное поведение функциональной связи между относительной деформацией ε и напряжением σ представлено графически на рис.1. При малых деформациях (прямая линия 0-П) наблюдается область пропорциональной упругой деформации. Здесь выполняется закон Гука. В области П-У деформация – также упругая, но закон Гука не справедлив. Начиная с точки У, вплоть до точки Т наблюдается область остаточных неупругих деформаций. Интервалу Т-Р соответствует область текучести, когда приложение незначительного усилия приводит к повышенной необратимой деформации. Вблизи точки Р текучесть прекращается, и для дальнейшего деформирования тела требуется приложение повышенного усилия. Однако это дополнительное усилие приводит к разрушению тела. Ниже перечислены названия особых точек и областей деформации:
П – предельная точка пропорциональной деформации,
У – предел упругости,
0-У – область упругих деформаций,
Т – предел текучести,
У-Т – область остаточных деформаций,
Т-Р – область текучести,
Р – предел прочности, точка разрыва.
2. Затухающие колебания
Если на колеблющееся тело действует сила трения, то энергия системы, амплитуда смещения и амплитуда скорости не остаются постоянными, а убывают, энергия расходуется на преодоление сил трения и превращается в тепло. Происходит затухание колебаний. Такие колебания не являются гармоническими, и дифференциальное уравнение движения, как это было показано в начале раздела, имеет вид:
3.
Билет 24