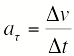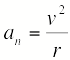Билет 19

1. Постулаты Бора.

2. Свободные колебания. Физический и математический маятник.

3. Второе начало термодинамики.

Постулаты Бора 1913 г.

1. Стационарные состояния: Атом может длительное время находится только в стационарных состояниях,

которые характеризуются дискретными значениями энергии. В этих состояниях атом не излучает.

2. Правило частот Бора: При переходе атома из стационарного состояния с большей энергией в

стационарное состояние с меньшей энергией происходит излучение кванта света (фотона) с энергией: hω=E₂-E₁

3. Дозволенные состояния: орбитальный момент электрона равен целому числу постоянной Планка : L=m_evr=nh v=nh/m_er

Свободные колебания. Физический и математический маятник.

Свободные или собственные колебания происходят в системе, предоставленной самой себе. Свободные колебания – всегда затухающие. Затухающими называются колебания, для которых амплитуда колебаний и, следовательно, энергия уменьшаются со временем. Затухание свободных колебаний механической системы происходит по причине рассеяния энергии под воздействием сил трения (не потенциальных сил сопротивления).

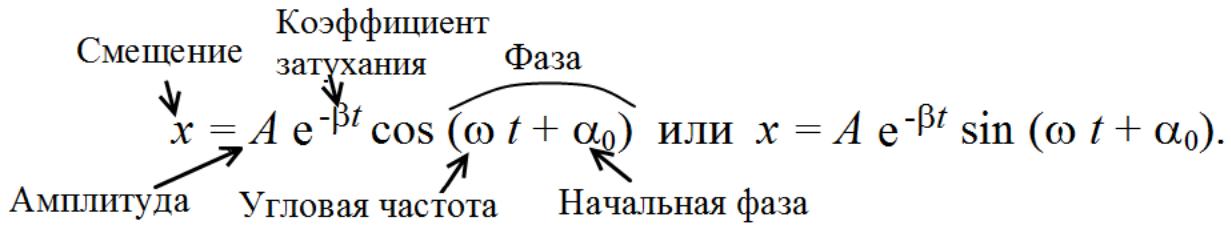
Динамика колебаний. Свободные колебания под действием квазиупругой силы

F_e=-kx сила упругости и F_r=-rv=-rẋ сила трения в вязкой среде.

ω₀=√k/m собственная угловая чистота колебаний системы и m- масса системы.

ẍ+ *x=0 уравнение собственных незатухающих колебаний для ᵝ=0

x=Acos(ω₀t+a₀)-решение

Энергия колебаний

Wк=mv²/2=m[Aω₀sin(ω₀t+a₀)]²/2=m A²sin²(ω₀t+a₀)/2

Wп=kx²/2=k[Acos(ω₀t+a₀)]²/2=kA²cos² (ω₀t+a₀)/2

Полная энергия: W=Wк+Wп=1/2m A²sin²(ω₀t+a₀)+1/2 kA²cos² (ω₀t+a₀)

Математический маятник.

ω₀=√g/l T0=2п/ ω₀=2П√l/g

Физический маятник

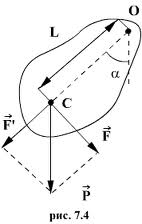
Если амплитуда колебаний   мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний:

.

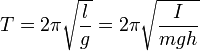3. Второе начало термодинамики.

   Чтобы термический коэффициент полезного действия теплового двигателя был  , должно быть выполнено условие  , т.е. тепловой двигатель должен иметь один источник теплоты, а это невозможно. Такой двигатель называется вечным двигателем второго рода.

       В 1824 г. Карно доказал, что для работы теплового двигателя необходимо не менее двух источников теплоты с различными температурами. Невозможность создания вечного двигателя второго рода подтверждается вторым началом термодинамики.

       Приведем некоторые формулировки второго начала термодинамики:

• Невозможен процесс, единственным результатом которого является превращение всей теплоты, полученной от нагревателя в эквивалентную ей работу (формулировка Кельвина).

• Невозможен вечный двигатель второго рода (формулировка Томпсона – Планка).

• Невозможен процесс, единственным результатом которого является передача энергии в форме теплоты от холодного тела к горячему (формулировка Клаузиуса).

при обратимом процессе имеет место равенство Клаузиуса:

;

при необратимом процессе имеет место неравенство Клаузиуса:

.

       Тогда для произвольного процесса,

.

       где знак равенства – для обратимого процесса; знак больше - для необратимого.

       Значит для замкнутой системы

.

      Это выражение – математическая запись второго начала термодинамики.

       Выражения и можно объединить:

.

      Энтропия замкнутой системы при любых происходивших в ней процессах не может убывать (или увеличивается, или остается неизменной).

       Первое и второе начала термодинамики в объединенной форме имеют вид:

.

Билет 20

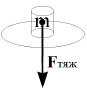
Сила притяжения(тяготения) Земли F тяг- силы, с которой

Земля притягивает тело(м.т.) согласно закону всемирного тяготения.

Сила тяжестиF тяж результирующий вектор всех сил, действующих на

тело, которое находится в свободном состоянии на Земле. Под действием силы

тяжести тело, не имеющее опоры или подвеса, движется с ускорением, которое

называется ускорением силы тяжести или ускорением свободного падения g.

Сила тяжести присутствует всегда и не зависит оттого, тело движется, или оно

покоится. Точка приложения силы тяжести приближенно совпадает с центром

инерции(масс) тела

2.При криволинейном движении скорость направлена по касательной к траектории. Поскольку направление скорости постоянно изменяется, то криволинейное движение - всегда движение с ускорением, в том числе, когда модуль скорости остается неизменным

В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением . Она характеризует изменение скорости по модулю.

Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением . Она характеризует изменение скорости по направлению.

Здесь R - радиус кривизны траектории в данной точке. Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения

3. Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решетку — систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. Рассматривая дифракцию Фраунгофера на щели, мы видели, что распределение интенсивности на экране определяется направлением дифрагированных лучей. Это означает, что перемещение щели параллельно самой себе влево или вправо не изменит дифракционной картины. Следовательно, если перейти от одной щели ко многим (к дифракционной решетке), то дифракционные картины, создаваемые каждой щелью в отдельности, будут одинаковыми.

Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т. е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.

Рассмотрим дифракционную решетку. На рис. 262 для наглядности показаны только две соседние щели MN и CD. Если ширина каждой щели равна а, а ширина непрозрачных участков между щелями b, то величина d=a+b называется постоянной (периодом) дифракционной решетки. Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления  одинаковы в пределах всей дифракционной решетки:

                                                

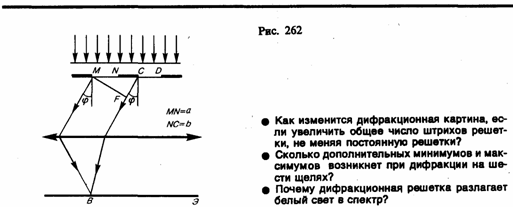
Очевидно, что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т. е. прежние (главные) минимумы интенсивности будут наблюдаться в направлениях, определяемых условием (179.2):

                                      

Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т. е. возникнут дополнительные минимумы. Очевидно, что эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей /2, 3/2, ..., посылаемых, например, от крайних левых точек М и С обеих щелей. Таким образом, с учетом (180.1) условие дополнительных минимумов:

Наоборот, действие одной щели будет усиливать действие другой, если

                                  

т. е. выражение (180.3) задает условие главных максимумов.

Таким образом, полная дифракционная картина, для двух щелей определяется из условий:

т. е. между двумя главными максимумами располагается один дополнительный мини­мум. Аналогично можно показать, что между каждыми двумя главными максимумами при трех щелях располагается два дополнительных минимума, при четырех ще­лях — три и т. д.

Если дифракционная решетка состоит из N щелей, то условием главных минимумов является условие (180.2), условием главных максимумов — условие (180.3), а условием дополнительных минимумов                        

где т' может принимать все целочисленные значения, кроме 0, N, 2N, .... т. е. кроме тех, при которых условие (180.4) переходит в (180.3). Следовательно, в случае N щелей между двумя главными максимумами располагается N–1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон.

Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, тем, следовательно, более интенсивными и более острыми будут максимумы. На рис. 263 качественно представлена дифракционная картина от восьми щелей. Так как модуль sin  не может быть больше единицы, то из (180.3) следует, что число главных максимумов

т. е. определяется отношением периода решетки к длине волны.