Билет 16

16.1 Момент инерции тела. Теорема о переносе осей (Штейнер)

Момент инерции

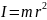. = Σi i = Σi mi

или I = ∫ d = ∫m dm

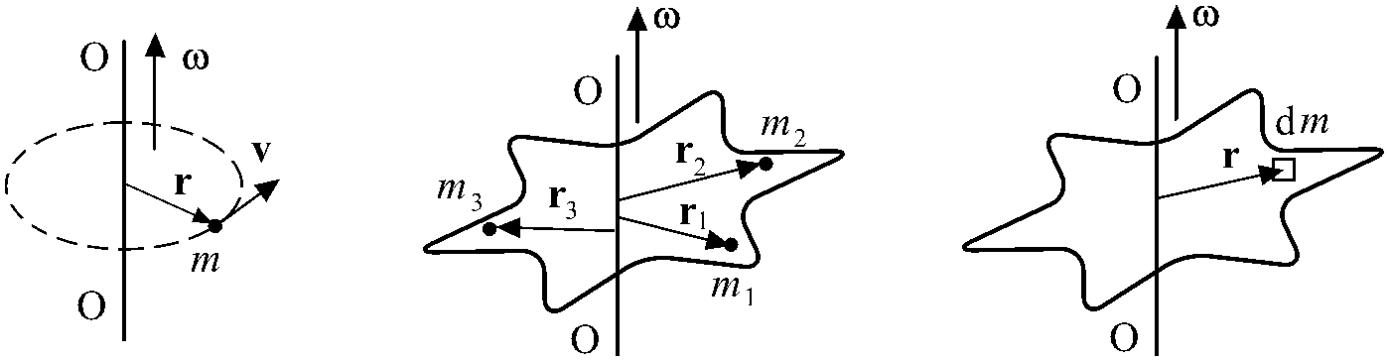
Теорема Гюйгенса-Штейнера

М омент инерции тела I относительно произвольной оси О'О' равен моменту инерции I₀ этого тела относительно оси ОО, проходящей через центр масс С параллельно данной оси, плюс произведение массы тела m на квадрат расстояния a между осями:

I = I₀ + ma²

16.2 Упругие свойства твердых тел. Типы деформаций. Закон Гука. Энергия упругой деформации

Упругие свойства твердых тел

Твердые тела сохраняют свой объем и форму, при любой попытке их деформировать возникают силы упругости.

Все возможные виды упругих деформаций твердого тела могут быть сведены к двум основным: растяжению-сжатию и сдвигу.

Типы деформаций

1. Продольное растяжение-сжатие

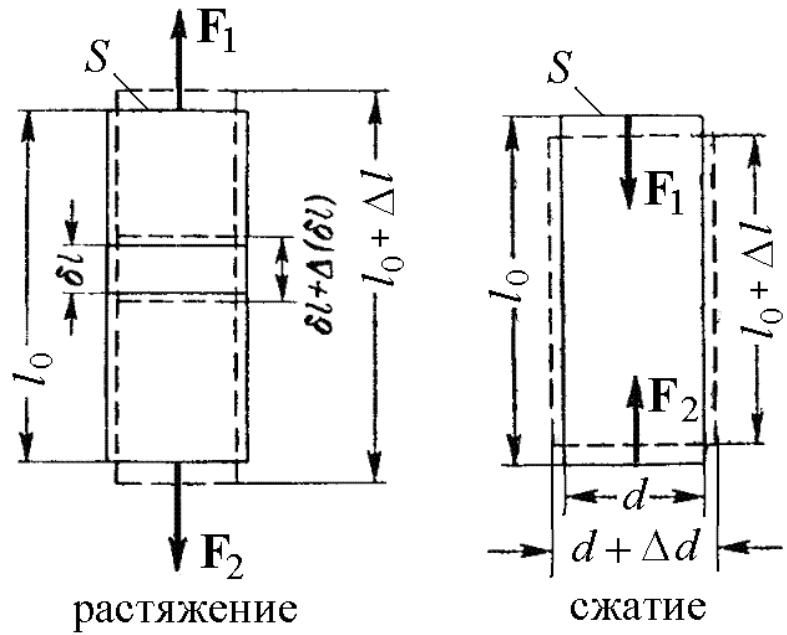
Если к концам однородного стержня постоянного сечения приложить направленные вдоль его оси силы F1 и F2, причем F1 = – F2, то первоначальная длина стержня l₀ получит положительное (при растяжении), либо отрицательное (при сжатии) приращение Δl = l – l₀ и станет равной l. При этом каждый произвольно выбранный элемент длины стержня δl получает приращение Δ(δl), пропорциональное его длине, так что для всех элементов стержня отношение Δ(δl)/δl оказывается одним и тем же. Естественно поэтому в качестве величины, характеризующей деформацию стержня, взять относительное изменение его длины: ε = Δl/l₀. Относительное удлинение ε является безразмерной величиной. В случае растяжения оно положительно, а в случае сжатия отрицательно

2. Деформация сдвига

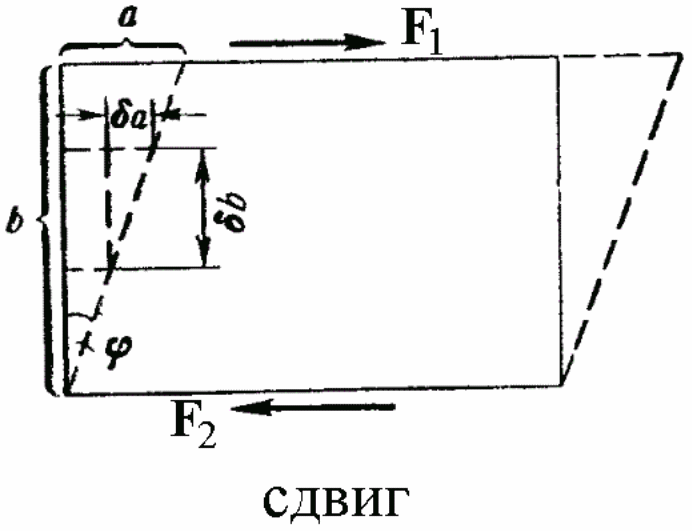
Возьмем однородное тело, имеющее форму прямоугольного параллелепипеда, и приложим к его противолежащим граням силы F1 и F2 (F1 = – F2), направленные параллельно этим граням. Если действие сил будет равномерно распределено по всей поверхности соответствующей грани S, то в любом сечении, параллельном этим граням, возникнет тангенциальное напряжение Ʈ = F / S. Под действием напряжения тело деформируется так, что одна грань смещается относительно другой грани на некоторое расстояние а. Если тело мысленно разбить на элементарные горизонтальные слои, то каждый слой окажется сдвинутым относительно соседних с ним слоев.

При деформации сдвига любая прямая, первоначально перпендикулярная к горизонтальным слоям, повернется на некоторый угол φ

γ=δɑ/δb=a/b=tgϕ

Величина γ называется относительным сдвигом. В силу малости угла ϕ можно положить tg ϕ≈ ϕ.

Следовательно γ= φ

γ= Ʈ

3. Кручение круглого стержня

Если круглый стержень закрепить одним концом неподвижно, а к другому концу приложить вращательный момент (момент пары сил) М, имеющий направление вдоль оси стержня, то стержень получит такую деформацию, при которой одно основание повернется по отношению к другому на некоторый угол φ

где l – длина стержня, R – радиус его сечения, G – модуль сдвига, М – вращательный момент (момент сил).

Закон Гука

Закон Гука для стержней из однородного материала – относительное удлинение при упругой деформации пропорционально силе, приходящейся на единицу площади поперечного сечения стержня:

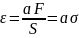
Энергия упругой деформации

Плотность энергии упругой деформации при сдвиге равна:

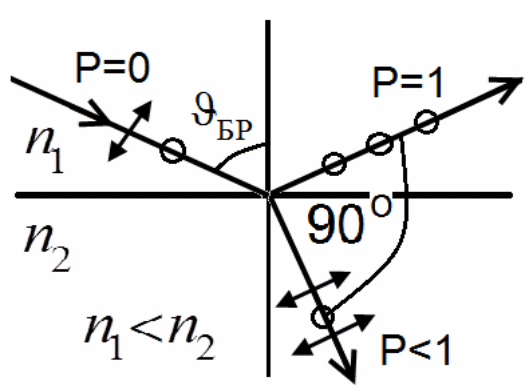
16.3Поляризация при отражении и преломлении. Угол Брюстера. Степень поляризации

Поляризация при отражении и преломлении. Угол Брюстера.

При падении света под углом Брюстера отраженный свет полностью поляризован, а степень поляризации преломленного луча достигает своего максимального значения, но меньшего единицы.

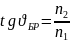
Степень поляризации

Р = 1 - плоско-поляризованный свет

Р = 0 - естественный свет

Р = 1 - частично-поляризованный свет