Розділ 2. Експериментальне дослідження ефективності диференціації завдань на уроках математики в поачаткових класах

2.1. Організація досліджень проведення уроків математики в початкових класах

Експериментальне дослідження з метою дослідження навчання математики учнів початкових класів та підвищення ефективності уроків за допомогою диференційованих завдань ми проводили у ЗОШ № 19 м. Рівне. Ним було охоплено 25 учнів 4-А класу (контрольного) і 24 учні 4-Б класу (експериментального).

Експериментальне дослідження проходило у три етапи:

• констатувальний експеримент, що передбачав аналіз організації уроків математики в 4 класі вчителем діагностику навчальних досягнень учнів 4-го класу з математики;

• формувальний етап, в процесі якого пропонувалася добірка уроків відповідно до календарного планування з використанням диференційованих завдань і проводилася систематична цілеспрямована робота із формування відповідних навичок та вмінь з використанням диференційованого підходу;

• контрольний етап – основна увага спрямовувалася на теоретичний аналіз і узагальнення результатів формувального експерименту, оформлення роботи та з’ясування подальших перспектив розробленої добірки завдань.

Дослідження організаційних умов вивчення математики у контрольному та експериментальному класах охоплювало відрізок навчальної програми із теми «Нумерація багатоцифрових чисел», який включав 7 уроків (таблиця 1) [20].

На перших трьох уроках ми спостерігали за діяльністю вчителя, врахуванням у роботі на уроці особливостей сприйняття кожного учня. Перший урок «Тематичне опитування. Контроль навчальних досягнень учнів з теми «Нумерація чотирицифрових та п’ятицифрових чисел» проводився у формі контрольної роботи, яка мала на меті перевірку навчальних досягнень учнів четвертого класу з попередньої частини теми, а саме вміння дітей працювати з чотирицифровими та п’ятицифровими числами.

Наступні два уроки ми відвідали з метою аналізу діяльності вчителя. Один з них ми відвідали у контрольному класі, наступний – в експериментальному. Нами відмічено, зокрема, що уроки проводяться вчителями на належному методичному та організаційному рівні, майже всі учні задіяні у роботі, вчителі використовують наочність, ігрові форми роботи. Проте диференційовані завдання на уроках не проводяться, отже не враховані психологічні особливості та рівні здібностей кожної дитини.

Таблиця 1

Календарне планування відвіданих та проведених уроків

№ з/п	Тема уроку	№№ завдань	Дата
27.	Тематичне опитування. Контроль навчальних досягнень учнів з теми «Нумерація чотирицифрових та п'ятицифрових чисел».
28.	Аналіз тематичного опитування. Нумерація шестицифрових чисел: читання і записування шестицифрових чисел у межах 200000. Повторення письмового ділення на одноцифрове число. Задачі, які включають знаходження частини числа.	194 – 203
29.	Читання і записування шестицифрових чисел в межах 200 тисяч. Лічба сотнями тисяч до 10 сотень тисяч. Мільйон. Задачі, обернені до задач на знаходження суми двох добутків.	204 – 212
30.	Нумерація шестицифрових чисел. Читання і записування, визначення числа тисяч у числі. Задачі, обернені до задач на знаходження суми двох добутків.	213 – 220
31.	Нумерація шестицифрових чисел. Поняття класу. Таблиця розрядів і класів. Множення і ділення на одноцифрові і двоцифрові числа.	221 – 228
32.	Читання і записування шестицифрових чисел. Множення і ділення на 10, 100 і 1000.
33.	Визначення числа десятків, сотень, тисяч, десятків тисяч і сотень тисяч у багатоцифрових числах. Розв'язування задач.	239 – 249

На основі результатів контрольної роботи ми визначили рівні навчальних досягнень учнів обох класів, результати яких представлені у додатку А.

Оцінювання – це процес встановлення рівня навчальних досягнень учня и оволодінні змістом предмета порівняно з вимогами чинних програм. Об’єктивність і точність оцінок забезпечуються критеріями оцінювання. І якими критеріями є: якість знань, рівень сформованості вмінь, рівень оволодіння досвідом творчої діяльності.

На основі вказаних критеріїв виділяються чотири інтегрованих рівні досягнень учнів початкових класів:

I рівень – початковий (1 - 3 бали);

II рівень – середній (4 - 6 балів);

I11 рівень – достатній (7 - 9 балів);

IV рівень – високий (10 - 12 балів).

Подамо рекомендації для оцінювання усних відповідей.

Високий рівень – учень правильно відповідає на всі запитання, самостійно застосовує на практиці окремі теоретичні положення; без помилок і доволі швидко обчислює, свідомо використовуючи властивості арифметичних дій; самостійно розв'язує задачі й пояснює хід розв'язування; безпомилково називає відомі геометричні фігури, вміє виконати практичне завдання — виміряти чи накреслити; виконує прості вправи, пов'язані з буквеною символікою (читання буквених виразів, знаходження їх значень за даними числовими значеннями букв, розв'язування рівнянь відповідно до програми).

Достатній рівень – коли відповідь загалом задовольняє попередні вимоги, але учень допускає окремі неточності у поясненні математичних фактів, прийомів обчислень; не завжди використовує в обчисленнях раціональні прийоми, часом припускається негрубих помилок; працюючи над задачею, не зовсім точно пояснює хід розв'язування чи результати дій; допускає огріхи, виконуючи вимірювання і креслення. Усі ці недоліки школярі легко виправляють за вказівкою вчителя.

Середній рівень – якщо учень правильно розв'язує більшість запропо­нованих прикладів, але не вміє пояснити прийом обчислення; допускає в обчисленнях помилки, які виправляє за допомогою вчителя; хоч і поми­ляється у розв'язуванні задачі, поясненні, проте за допомогою вчителя виконує завдання.

Початковий рівень – учень не засвоїв більшої частини програмового матеріалу, не може впоратися з розв'язуванням задачі та обчисленнями навіть за допомогою класовода.

Норми оцінювання письмових робіт з математики подані у додатку 2.

Взявши за основу рівні навчальних досягнень учнів обох класів із таблиць додатків 1.1 та 1.2 ми побудували узагальнену таблицю 2.

Таблиця 2

Рівні сформованості навчальних досягнень з математики учнів контрольного та експериментального класів на констатувальному етапі дослідження, у %

Рівні сформованості навчальних досягнень з математики	Високий	Достатній	Середній	Низький
Відсоткове співвідношення учнів контрольного класу з різними рівнями навчальних досягнень	16	52	24	8
Відсоткове співвідношення учнів експериментального класу з різними рівнями навчальних досягнень	17	58	17	8

Таким чином, аналіз результатів діагностики навчальних досягнень учнів четвертого класу на основі виконання контрольної роботи дозволив виявити, що рівень успіхів у контрольному та експериментальному класах є практично однаковим. Так, 16% учнів контрольного класу показали високий рівень досягнень, достатній рівень сформований у більшості учнів класу – 52%, середній та низький рівні продемонстрували 24% та 8% дітей відповідно.

В експериментальному класі результати були такими: 17% продемонстрували високий рівень досягнень, 58% виявили достатній рівень, 17% показали середній рівень, 8% справились із завданнями контрольної, виявивши низький рівень.

Усі отримані дані наочно демонструє діаграма на рисунку 1.

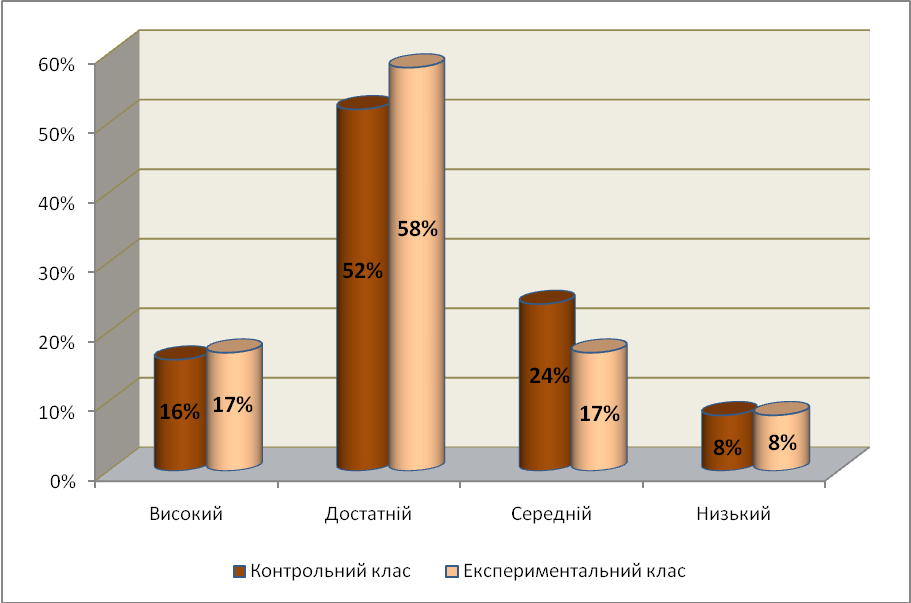
Рис.1. Рівні навчальних досягнень учнів контрольного та експериментального класів на констатувальному етапі дослідження

Дані констатувального етапу дослідження доводять, що навчальні досягнення учнів обох класів сформовані на однаковому рівні, у переважної більшості з них рівень знань, умінь і навичок є достатнім. Тож виникає необхідність проведення формувальної роботи для підвищення ефективності навчання математики у початкових класах з урахуванням особливостей кожного учня, тобто з використанням диференційованих завдань.