Вопрос 7. Электромагнитные волны в веществе. Распространение света в веществе. Дисперсия света. Поглощение света. Прозрачные среды. Поляризация волн при отражении.
ЭЛЕКТРОМАГНИ́ТНЫЕ ВО́ЛНЫ - электромагнитные колебания, распространяющиеся в пространстве с конечной скоростью, зависящей от свойств среды. Электромагнитной волной называют распространяющееся электромагнитное поле.
Существование электромагнитных волн было предсказано М. Фарадеем еще в 1832 г.Дж. Максвелл в 1865 г. в результате анализа предложенной им системы уравнений,описывающей электромагнитное поле, теоретически показал, что электромагнитное поле в вакууме может существовать и в отсутствие источников — зарядов и токов. Поле без источников имеет вид волн, распространяющихся с конечной скоростью, которая в вакууме равна скорости света: с = 2997924581,2 м/с. Совпадение скорости распространения электромагнитных волн в вакууме с измеренной ранее скоростью света позволило Максвеллу сделать вывод о том, что свет представляет собой электромагнитные волны. Подобное заключение в дальнейшем легло в основу электромагнитной теории света.
В отличие от статического электрического и магнитного полей, которые не существуют в отрыве от источника, электромагнитная волна существует без источника в том смысле, что после ее излучения электромагнитное поле не связано с источником.
Независимо от природы электромагнитные волны обладают общими свойствами. На скорость и характер распространения электромагнитных волн существенно влияет среда, в которой они распространяются. Электромагнитные волны могут испытывать преломление, в реальных средах имеет место дисперсия волн, вблизи неоднородностей наблюдаются дифракция волн, интерференция волн, полное внутреннее отражение и другие явления, свойственные волнам любой природы.
Если среда неоднородна или содержит поверхности, на которых изменяются ее электрические или магнитные свойства, или если в пространстве имеются проводники, то тип возбуждаемых и распространяющихся электромагнитных волн может существенно отличаться от плоской линейно-поляризованной волны. Электромагнитные волны могут распространяться вдоль направляющих поверхностей (поверхностные волны), в передающих линиях и в полостях, образованных хорошо проводящими стенками.
Электромагнитные волны различных частотных диапазонов характеризуются различными способами возбуждения. Источником электромагнитных волн может быть любой электрический колебательный контур или проводник, по которому течет переменный электрический ток, так как для возбуждения электромагнитных волн необходимо создать в пространстве переменное электрическое поле или соответственно переменное магнитное поле. На расстоянии от источника много большем l образуется волновая зона (зона излучения), где распространяются сферические электромагнитные волны. Они поперечные и линейно поляризованы. Монохроматическую и когерентную волну излучает гармонический осциллятор. Ее рассматривают как монохроматическую волну, у которой постоянна частота колебаний. Свет представляет собой электромагнитные волны определенной длины волны. Опыты, в которых была открыта поляризация света, указывают на то, что эти волны поперечные.
Распространение света в веществе Для анализа распространения света в оптически плотном веществе рассмотрим модель распространения света. Фотоны движутся прямолинейно в интервалах между столкновениями с атомами со скоростью "с" относительно эфира, при столкновениях фотоны поглощаются электронами атома и затем испускаются, причем время ', характеризующее этот процесс, определяется временем перехода электрона в возбужденное состояние и обратно. Обозначив через L'0 среднюю длину пути, проходимого фотоном перед поглощением (в системе отсчета, связанной с веществом), определим коэффициент преломления для движущегося вещества (в его системе отсчета) из уравнения:
L'0 /(c'/n')=L'0 /c'+' |
, |
(28) |
Величины L'0 и ' не зависят от значения абсолютной скорости, так как измерители длины и времени находятся в системе отсчета вещества. При нулевой абсолютной скорости вещества (с'=с, n'=n) из (28) имеем: n=1+p, где p='c/L'0 . Отсюда и из (28), с учетом выражения (24) для скорости света с'=с/[1 +(v1 /c)сos'], следует формула для коэффициента преломления в движущемся веществе:
n' =1+ |
p |
; или |
n' = |
n+(v1 /c)сos' |
(29) |
|
|
||||
1+(v1 /c)сos' |
1+(v1 /c)сos' |
где '- угол между вектором абсолютной скорости v1 и направлением распространения света. Показатель преломления n, входящий в (29), - это коэффициент преломления света в неподвижном (относительно эфира) веществе. Он совпадает с показателем преломления в движущемся веществе, измеренным интерференционными методами. Действительно, рассмотрим интерференцию двух лучей, проходящих расстояние L', причем один из лучей проходит этот путь через вещество, а второй - в вакууме. Разность времени распространения света для этих лучей согласно (29) составляет:
L' n'/с' - L'/с'=L'[n + (v1 /c)сos'] /c - L'[1 + (v1 /c)сos' ]/с=L'(n-1)/c. |
Выражение (29) может быть использовано для обобщения инварианта (1) на распространение света в веществе:
t'++t'_= L' n'+ /с'++ L' n'_ /с'_= 2L' n/c |
, |
(30) |
где n'+ и n'_ - показатели преломления света n' для взаимно противоположных направлений распространения, под углами ' и (' + ) к вектору абсолютной скорости.
|
Рис.
3. Схема опыта Физо.В качестве теста для модели распространения света в веществе и предлагаемой теории рассмотрим опыт Физо. Как известно [3], опыт Физо, включает две параллельные оптические линии (рис.3), вдоль которых во взаимно противоположных направлениях движется вода. В эксперименте установлена связь между скоростью течения воды и сдвигом фаз двух лучей света, проходящих обе оптические линии по течению воды и против течения:
=(4Lu0 /c)(n2-1) , |
где u0-скорость течения воды относительно Земли, - длина световой волны, n - коэффициент преломления света в воде. Покажем, что этот результат, впервые полученный в СТО, находит естественное объяснение в рамках изложенных методик. Согласно (15), абсолютная скорость воды равна: v ± u0 2 . Здесь предполагается, что направления движения воды и Земли совпадают вдоль одной оптической линии-(a) и противоположны вдоль другой линии-(b). Для скорости света луча 1, распространяющегося по течению воды, в системе отсчета воды из (29,24) получаем:
с'+1=с/(n + v/c + u0 2/c) - на участке оптической линии (a), и с'-1=с/(n - v/c + u0 2/c) -на участке оптической линии (b). |
Аналогично для скорости света луча 2, распространяющегося против течения, имеем:
с'-2=с/(n - v/c - u0 2/c) - на линии (a), и с'+2=с/(n + v/c - u0 2/c) - на линии (b). |
При переходе в земную систему отсчета, для указанных скоростей света имеем по закону сложения скоростей (17) (в приближении порядка v/c):
с-1=[с/(n - v/c + u0 /c)]+u0 ; с+1=[с/(n + v/c + u0 /c)]+u0 с-2=[с/(n - v/c - u0 /c)] -u0 ; с+2=[с/(n + v/c - u0 /c)] -u0 . |
Для разности времени движения соответствующих лучей получаем:
T-2 -T+1=L /с-2 - L/с+1 2L[u0 (n2-1)-v]/c2; T+2 -T-1= L/с+2 - L/с-1 2L[u0 (n2-1)+v]/c2. |
Итак,
T= T+2 +T-2 - (T+1+T-1 )=4Lu0 (n2-1)/c2. |
Диспе́рсия све́та (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты(или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты). Экспериментально открыта Ньютоном около 1672 года, хотя теоретически достаточно хорошо объяснена значительно позднее.
Пространственной дисперсией называется зависимость тензора диэлектрической проницаемости среды от волнового вектора. такая зависимость вызывает ряд явлений, называемых эффектами пространственной поляризации.
Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является неодинаковая скорость распространения лучей света c различной длиной волны в прозрачном веществе —оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и следовательно цвета). Обычно чем больше частота волны, тем больше показатель преломления среды и меньше ее скорость света в ней:
у красного цвета максимальная скорость в среде и минимальная степень преломления,
у фиолетового цвета минимальная скорость света в среде и максимальная степень преломления.
Однако в некоторых веществах (например в парах йода) наблюдается эффект аномальной дисперсии, при котором синие лучи преломляются меньше, чем красные, а другие лучи поглощаются веществом и от наблюдения ускользают. Говоря строже, аномальная дисперсия широко распространена, например, она наблюдается практически у всех газов на частотах вблизи линий поглощения, однако у паров йода она достаточно удобна для наблюдения в оптическом диапазоне, где они очень сильно поглощают свет.
Дисперсия света позволила впервые вполне убедительно показать составную природу белого света.
Белый свет разлагается на спектр и в результате прохождения через дифракционную решётку или отражения от нее (это не связано с явлением дисперсии, а объясняется природой дифракции). Дифракционный и призматический спектры несколько отличаются: призматический спектр сжат в красной части и растянут в фиолетовой и располагается в порядке убывания длины волны: от красного к фиолетовому; нормальный (дифракционный) спектр — равномерный во всех областях и располагается в порядке возрастания длин волн: от фиолетового к красному.
По аналогии с дисперсией света, также дисперсией называются и сходные явления зависимости распространения волн любой другой природы от длины волны (или частоты). По этой причине, например, термин закон дисперсии, применяемый как название количественного соотношения, связывающего частоту и волновое число, применяется не только кэлектромагнитной волне, но к любому волновому процессу.
Дисперсией объясняется факт появления радуги после дождя (точнее тот факт, что радуга разноцветная, а не белая).
Дисперсия является причиной хроматических аберраций — одних из аберраций оптических систем, в том числе фотографических и видео-объективов.
Коши пришел к формуле, выражающей зависимость показателя преломления среды от длины волны:
где:
—
длина
волны в вакууме;a, b, c, … — постоянные, значения которых для каждого вещества должны быть определены в опыте. В большинстве случаев можно ограничиться двумя первыми членами формулы Коши.
Поглощением (абсорбцией) света называется явление потери энергии световой волной, проходящей через вещество. В результате поглощения интенсивность света при прохождении через вещество уменьшается.
Поглощение энергии света в веществе описывается законом Бугера:
I=I0e−ax,
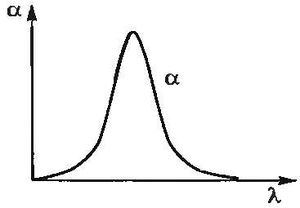
где I0 и I — интенсивности плоской монохроматической световой волны на входе и выходе слоя поглощающего вещества толщиной x,α — коэффициент поглощения, зависящий от длины волны света, химической природы и состояния вещества и не зависящий от интенсивности света при слабых световых потоках.
На рисунке 17.34 представлена типичная зависимость коэффициента поглощения от длины волны света. Зависимостью коэффициента поглощения от λ объясняется окрашенность поглощающих тел. Например, стекло, слабо поглощающее красные и оранжевые лучи и сильно поглощающее зеленые и синие, при освещении белым светом будет казаться красным. Если на такое стекло направить зеленый и синий свет, то из-за сильного поглощения света этих длин волн стекло будет казаться черным. Зависимость коэффициента поглощения от длины волны света используется для изготовления светофильтров, которые в соответствии с химическим составом пропускают свет только определенных длин волн, поглощая остальные.
Прозрачные среды (оптические стекла, очень чистые прозрачные жидкости и газы) почти не рассеивают света; это объясняется тем, что вторичные волны, излучаемые частицами среды, вследствие интерференции взаимно гасятся по всем направлениям, кроме направления распространения проходящего света. При этом, как показал Л. И. Мандельштам, важна однородность среды, так как для полного гашения необходима не только когерентность, но и равенство интенсивностей интерферирующих волн.
Прозрачная среда считается оптически менее плотной, если скорость распространения света в ней больше, чем в воздухе, и оптически более плотной если скорость в ней меньше, чем в воздухе.
Воздух является практически прозрачной средой, твердые тела и жидкости - непрозрачны. Многие тела прозрачны только для определенных длин волн. Так, например, оконное стекло пропускает световые лучи и почти непрозрачно для ультрафиолетового ( оказывающего наиболее сильное химическое воздействие) и длинноволнового инфракрасного излучения. Кварц прозрачен для светового и ультрафиолетового излучения и непрозрачен для инфракрасного. Этими свойствами оконного стекла и кварца широко пользуются в технике.
Если в прозрачной среде диспергированы частицы, то на длине волны, для которой показатели преломления среды и частиц одинаковы, будет наблюдаться эффект Христиансена. Он состоит в резком увеличении пропускания частот, для которых среда оказывается оптически гомогенной. Пропускание других частот будет уменьшено за счет рассеяния на частицах.
Поляризация волн при отражении
Поляризованный свет можно получить, используя отражение или преломление света от диэлектрических изотропных сред (например, от стекла). Если угол падения света на границу раздела двух диэлектриков отличен от нуля, отраженный и преломленный лучи оказываются частично поляризованными. В отраженном луче преобладают колебания, перпендикулярные плоскости падения (на рис. 5.9 эти колебания обозначены точками), в преломленном луче – колебания, параллельные плоскости падения (на рис. 5.9 они изображены двусторонними стрелками).
С
тепень
поляризации того и другого луча зависит
от угла падения луча. У каждой пары
прозрачных сред существует такой угол
падения, при котором отраженный свет
становится полностью плоскополяризованным,
а преломленный луч остается частично
поляризованным, но степень его поляризации
при этом угле максимальна (рис. 5.10).
Этот угол называется углом Бpюстеpа.
Угол Брюстера определяется из условия
,
где 
–
относительный показатель преломления
двух сред. Можно показать, что при падении
волны под углом Брюстера отраженный и
преломленный лучи взаимно перпендикулярны.
Таким образом, пластинка диэлектрика сортирует лучи естественного света, отражая преимущественно лучи с одним направлением колебаний и пропуская перпендикулярные колебания.
Рис. 5.11а |
Рис. 5.11б |
Основными источниками поляризованного света в окружающей нас среде являются такие яркие горизонтальные поверхности как водная гладь, мокрый асфальт (рис. 5.11а), снег, лед (рис. 5.11б), стеклянные поверхности (рис. 5.11в). По характеру воздействия на глаз или фотоплёнку плоскополяризованный свет ничем не отличается от неполяризованного.
Рис. 5.11в |
Рис. 5.11г |
8.Уравнение Шредингера. Задание состояние микрочастицы, волновая функция, её статистический смысл. Суперпозиция состояний в квантовой теории. Амплитуда вероятности. Стационарное уравнение Шредингера, стационарные состояния. Частица в однородной прямоугольной яме. Прохождение частицы над и под барьером. Гармонический осциллятор. Элементы квантовой электроники. Волновые функций стационарных состояний.
Уравне́ниеШрёдингера — уравнение, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона вклассической механике. Его можно назвать уравнением движения квантовой частицы. Установлено Эрвином Шрёдингером в 1926 году.
Уравнение Шрёдингера предназначено для частиц без спина, движущихся со скоростями много меньшими скорости света. В случае быстрых частиц и частиц со спином используются его обобщения (уравнение Клейна — Гордона, уравнение Паули, уравнение Дирака и др.)
В начале XX века учёные пришли к выводу, что между предсказаниями классической теории и экспериментальными данными об атомной структуре существует ряд расхождений. Открытие уравнения Шрёдингера последовало за революционным предположением де Бройля, что не только свету, но и вообще любым телам (в том числе и любым микрочастицам) присущи волновые свойства.
Исторически окончательной формулировке уравнения Шрёдингера предшествовал длительный период развития физики. Оно является одним из важнейших уравнений физики, объясняющих физические явления. Квантовая теория, однако, не требует полного отказа от законов Ньютона, а лишь определяет границы применимости классической физики. Следовательно, уравнение Шрёдингера должно согласовываться с законами Ньютона в предельном случае. Это подтверждается при более глубоком анализе теории: если размер и масса тела становятся макроскопическими и точность слежения за его координатой много хуже стандартного квантового предела, прогнозы квантовой и классической теорий совпадают, потому что неопределённый путь объекта становится близким к однозначной траектории.
Наиболее общая форма уравнения Шрёдингера — это форма, включающая зависимость от времени[1] :
-
Зависимое от времени уравнение (общий случай)
Волнова́яфу́нкция, или пси-функция — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):
где 
—
координатный базисный вектор, а 
—
волновая функция в координатном
представлении.
Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятностинахождения частицы в данной точке пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.
Волновая функция (или вектор состояния) – комплексная функция, описывающая состояние квантовомеханической системы. Её знание позволяет получить максимально полные сведения о системе, принципиально достижимые в микромире. Так с её помощью можно рассчитать все измеряемые физические характеристики системы, вероятность пребывания её в определенном месте пространства и эволюцию во времени. Волновая функция может быть найдена в результате решения волнового уравнения Шредингера.
Статическая интерпретация волновой функции
На основании статистической интерпретации вероятность нахождения частицы в
момент времени t с координатами x и x+dx, y и y+dy, z и z+dz определяется
интенсивностью волновой функции, т.е. квадратом пси-функции. Поскольку в
общем случае ψ - комплексная функция, а вероятность должна быть всегда
действительной и положительной величиной, то за меру интенсивности
принимается квадрат модуля волновой функции.
Физический смысл ψ - функции
Вероятность dW нахождения частицы в элементе объема dV в момент времени t
2
dW = ψ dV .
Ква́нтоваясуперпози́ция (когерентная суперпозиция) — это суперпозиция состояний, которые не могут быть реализованы одновременно склассической точки зрения, это суперпозиция альтернативных (взаимоисключающих) состояний. Принцип существования суперпозиций состояний обычно называется в контексте квантовой механики просто принципом суперпозиции.
Если
функции 
и 
являются
допустимыми волновыми функциями,
описывающими состояние квантовой
системы, то их линейная суперпозиция, 
,
также описывает какое-то состояние
данной системы. Если измерение какой-либо
физической величины 
в
состоянии 
приводит
к определённому результату 
,
а в состоянии 
—
к результату 
,
то измерение в состоянии 
приведёт
к результату
или
с
вероятностями 
и 
соответственно.
Из принципа суперпозиции также следует, что все уравнения на волновые функции (например, уравнение Шрёдингера) в квантовой механике должны быть линейными.
Любая наблюдаемая величина (например, положение, импульс или энергия частицы) является собственным значением эрмитова линейного оператора, соответствующим конкретному собственному состоянию этого оператора, то есть определённой волновой функции, действие оператора на которую сводится к умножению на число — собственное значение. Линейная комбинация двух волновых функций — собственных состояний оператора также будет описывать реально существующее физическое состояние системы. Однако для такой системы наблюдаемая величина уже не будет иметь конкретного значения, и в результате измерения будет получено одно из двух значений с вероятностями, определяемыми квадратами коэффициентов (амплитуд), с которыми базисные функции входят в линейную комбинацию. (Разумеется, волновая функция системы может быть линейной комбинацией и более чем двух базисных состояний, вплоть до бесконечного их количества).
Важными следствиями квантовой суперпозиции являются различные интерференционные эффекты (см. опыт Юнга, дифракционные методы), а для составных систем — зацепленные состояния.
Популярный пример парадоксального поведения квантовомеханических объектов с точки зрения макроскопического наблюдателя — кот Шрёдингера, который может представлять собой квантовую суперпозицию живого и мёртвого кота. Впрочем, достоверно ничего не известно о применимости принципа суперпозиции (как и квантовой механики вообще) к макроскопическим системам.
Частица в одномерной прямоугольной “потенциальной яме” с бесконечно высокими “стенками”.
Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной “потенциальной яме” с бесконечно высокими “стенками”. Такая “яма” описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)
где l - ширина “ямы”, а энергия отсчитывается от ее дна (рис. 2).
Рис. 2
Уравнение Шредингера (7.5) в случае одномерной задачи запишется в виде
.
(8.1)
По условию задачи (бесконечно высокие “стенки”), частица не проникает за пределы “ямы”, поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами “ямы” равна нулю. На границах “ямы” (при х=0 и х=l) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид
(8.2)
В
пределах “ямы” (
уравнение
Шредингера (8.1) сведется к уравнению
,
или
(8.3)
где
(8.4)
Общее решение дифференциального уравнения (8.3):
(8.5)
Условие 
(8.2)
выполняется только при 
где
n – целые числа, т. е. необходимо, чтобы
.
(8.6)
Из выражений (8.4) и (8.6) следует, что
(8.7)
т.е. уравнение Шредингера, описывающее движение частицы в “потенциальной яме” с бесконечно высокими “стенками”, удовлетворяется только при собственных значениях Еn, зависящих от целого числа n. Следовательно, энергия частицы в “потенциальной яме” с бесконечно высокими “стенками” не может быть произвольной, а принимает лишь определенные дискретные значения, т. е. квантуется. Квантованные значения энергии Е„ называются уровнями энергии, а число n, определяющее энергетические уровни частицы, называется квантовым числом. Таким образом, микрочастица в “потенциальной яме” с бесконечно высокими “стенками” может находиться только на определенном энергетическом уровне En, или, как говорят, частица находится в определенном квантовом состоянии n.
Подставив в (8.5) значение k из (8.6) найдем собственные функции:
Постоянную интегрирования А определим из условия нормировки (6.3), которое для данного случая запишется в виде
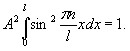
В
результате интегрирования
получим 
,
а собственные функции будут иметь вид
(8.8)
Рис. 3
Графики
собственных функций (220.8), соответствующие
уровням энергии (8.7) при n = 1, 2. 3, приведены
на рис.3. а. На рис.3, б изображена плотность
вероятности обнаружения частицы от
“стенок” ямы, равная 
для
n – 1, 2 и 3. Из рисунка следует, что.
например, в квантовом состоянии с п = 2
частица не может находиться в середине
“ямы”, в то время как одинаково часто
может пребывать в ее левой и правой
частях. Такое поведение частицы указывает
на то, что представления о траекториях
частицы в квантовой механике
несостоятельны.
Из выражения (8.7) вытекает, что энергетический интервал между двумя соседними уровнями равен
(8.9)
Например,
для электрона при размерах ямы 
м
(свободные электроны в металл 
Дж
эВ
т.е. энергетические уровни расположены
столь тесно, что спектр практически
можно считать непрерывным. Если же
размеры ямы соизмеримы с атомными),
то для электрона 
Дж=
эВ,
т. е. получаются явно дискретные -значения
энергии (линейчатый спектр). Таким
образом, применение уравнения
Шредингера к частице в «потенциальной
яме» с бесконечно высокими «стенками»
приводит к квантованным значениям
энергии, в то время как классическая
механика на энергию этой частицы никаких
ограничений не накладывает.
Стационарное уравнение Шрёдингера
Форма
уравнения Шрёдингера показывает, что
относительно времени его решение должно
быть простым, поскольку время входит в
это уравнение лишь через первую
производную в правой части. Действительно,
частное решение для специального случая,
когда 
не
является функцией времени, можно записать
в виде:
где
функция 
должна
удовлетворять уравнению:
которое
получается из уравнения Шрёдингера (1) при
подстановке в него указанной выше
формулы для 
(2).
Заметим, что это уравнение вообще не
содержит времени; в связи с этим оно
называется стационарным
уравнением Шрёдингера (уравнение
Шрёдингера, не содержащее времени).
Выражение (2) является
лишь частным
решением зависящего
от времени уравнения Шрёдингера (1),
общее решение представляет собой линейную
комбинацию всех
частных решений вида (2).
Зависимость функции 
от
времени проста, но зависимость её от
координаты не всегда имеет элементарный
вид,
так как уравнение (3) при
одном выборе вида потенциальной
функции 
совершенно
отличается от того же уравнения при
другом выборе этой функции. В
действительности, уравнение (3) может
быть решено аналитически лишь для
небольшого числа частных типов функции
.
Важное
значение имеет интерпретация величины 
в
уравнении (2).
Она производится следующим путём:
временна́я зависимость функции
в
уравнении (2) имеетэкспоненциальный характер,
причём коэффициент при 
в
показателе экспоненты выбран так, что
правая часть уравнения (3) содержит
просто постоянный множитель
.
В левой же части уравнения (3) функция 
умножается на
потенциальную энергию
.
Следовательно, из соображений размерности вытекает,
что величина
должна
иметь размерностьэнергии.
Единственной величиной с размерностью
энергии, которая постоянна в механике,
является полная (сохраняющаяся) энергия
системы; таким образом, можно предполагать,
что
представляет
собой полную энергию. Согласно физической
интерпретации уравнения
Шрёдингера,
действительно
является полной энергией частицы при
движении, описываемом функцией
.
Гармони́ческийосцилля́тор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука):
где k — коэффициент жёсткости системы.
Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.
Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.
Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.
Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор