Интерференция света в тонких плёнках

Рассмотрим интерференцию волн, наблюдаемую при отражении света от тонких пленок (рис. 12).

В этом случае интерферировать будут волны 1 и 2, отразившиеся от верхней и нижней поверхностей пленки. При этом разность хода

,

Нетрудно показать, что учтено, что при отражении от оптически более плотной среды, добавляется к соответствующему оптическому пути.

.

Условие максимума интерференции в этом случае:

; … (39)

условие минимума

; … (40)

Тонкая пленка окрашивается в те цвета, длина волны которых удовлетворяет условию максимума.

Оптическая разность хода зависит от двух параметров – толщины пленки и угла падения света .

Можно выделить два типа интерференционных схем.

В случае, если толщина пленки неизменна, одинаковая разность хода будет соответствовать равным углам наклона . Такие интерференционные полосы называются полосами равного наклона. Так при падении света от точечного монохроматического источника на тонкую пленку в отраженном свете будут наблюдаться кольца, соответствующие равным углам падения.

Если параллельный пучок света падает на пластинку с разной толщиной, одинаковая разность хода соответствует областям с одинаковой толщиной. Такие интерференционные картины называются полосами равной толщины.

Примером могут служить интерференционные полосы, наблюдаемые на клине, или кольца Ньютона, наблюдаемые при интерференции в воздушном клине, образуемом между стеклянной линзой и стеклянной подложкой.

Интерферометры

Интерферометр — измерительный прибор, принцип действия которого основан на явлении интерференции. Принцип действия интерферометра заключается в следующем: пучок электромагнитного излучения (света, радиоволн и т. п.) с помощью того или иного устройства пространственно разделяется на два или большее количество когерентных пучков. Каждый из пучков проходит различные оптические пути и возвращается на экран, создавая интерференционную картину, по которой можно установить смещение фаз пучков.

Вопрос 3

Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.

Дифракция первого и второго порядка как интерференция волн, образованных при падении плоской волны на непрозрачный экран с парой щелей. Стрелками показаны линии, проходящие через линии интерференционных максимумов

Принцип Гюйгенса — Френеля — основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности, световых.

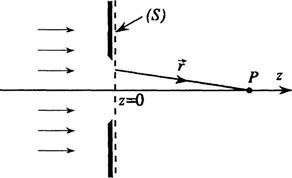
Принцип Гюйгенса-Френеля следует рассматривать как рецепт приближенного решения дифракционных задач. В основе его лежит допущение о том, что каждый элемент поверхности волнового фронта можно рассматривать как источник вторичных волн, распространяющихся во всех направлениях (рис. 2.1.). Эти волны когерентны, так как они возбуждены одной и той же первичной волной. Результирующее поле в точке наблюдения P может быть найдено как результат интерференции вторичных волн. В качестве поверхности вторичных источников может быть выбрана не только поверхность волнового фронта, но и любая другая замкнутая поверхность. При этом фазы и амплитуды вторичных волн определяются значениями фазы и амплитуды первичной волны.

В соответствии с принципом Гюйгенса–Френеля комплексная амплитуда поля в точке наблюдения P, обусловленная действием вторичных источников, заселяющих малый элемент поверхности ds, может быть записана в виде

Здесь – комплексная амплитуда поля первичной волны от источника на элементе ds, – длина волны (источник предполагается монохроматическим), – так называемый коэффициент наклона, зависящий от угла между нормалью к элементу поверхности ds и радиусом-вектором . В теории Френеля не было дано конкретного вида зависимости ; многие задачи теории дифракции света могут быть решены при весьма общих предположениях относительно этой зависимости. Важно только принять во внимание, что – медленно убывающая функция угла , принимающая значение K = 1 при . Вид функции был получен в теории Кирхгофа (1883 г.), развитой на основе анализа решений волнового уравнения. Таким образом, излучение вторичных источников не изотропно, хотя волновые фронты (то есть поверхности постоянной фазы) являются сферическими.

При более точной количественной формулировке принципа Гюйгенса–Френеля следовало бы учесть в (2.1) фазовый сдвиг на между излучением вторичных источников и первичной волной. Во многих задачах точное значение фазы колебаний не представляет интереса, поэтому не имеет смысла усложнять соотношение (2.1). Полное поле в точке P может быть найдено путем интегрирования (2.1) по всем вторичным источникам.

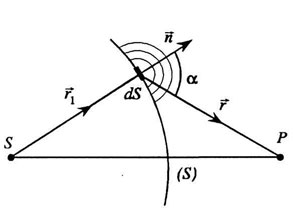
При решении дифракционных задач, когда речь идет о распространении световых волн вблизи препятствий, принцип Гюйгенса-Френеля следует дополнить постулатом Френеля о граничных условиях.

Рисунок 2.2. Граничные условия.

Пусть на экран с отверстием падает плоская волна (рис. 2.2). Постулат Френеля сводится к требованию заселения вторичными источниками только той части поверхности волнового фронта, которая не затенена экраном. Интегрирование выражения (2.1) следует выполнить по поверхности S, изображенной на рис. 2.2 пунктирной линией. При этом, там, где поверхность S затенена экраном, амплитуда вторичных волн равна нулю. На открытых частях экрана поле первичной волны предполагается невозмущенным. Постулат Френеля означает, что при интегрировании (2.1) комплексную амплитуду первичной волны следует заменить на , определяемую следующим образом:

Здесь – координаты в плоскости экрана. Обозначая через g комплексную амплитуду поля в точке наблюдения, можно записать

(2.2)

Постулат Френеля, как и принцип Гюйгенса–Френеля, носит приближенный характер. Его применение сильно упрощает дифракционную задачу и приводит к достаточно хорошим для практики результатам при условии, что размеры препятствий, на которых дифрагирует свет, а также расстояние между препятствием и точкой наблюдения велики по сравнению с длиной волны.

На основе принципа Гюйгенса-Френеля удается получить простое наглядное решение некоторых дифракционных задач (задачи с осевой симметрией, дифракция на одномерных препятствиях). В общем случае дифракционная задача сводится к вычислению интеграла (2.2)

 Метод зон Френеля

Френель предложил оригинальный метод разбиения волновой поверхности S на зоны, позволивший сильно упростить решение задач (метод зон Френеля).

      Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии  от точки M (рис. 9.2). Точки сферы S, находящиеся на расстояниях , , и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля.

      Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M    .

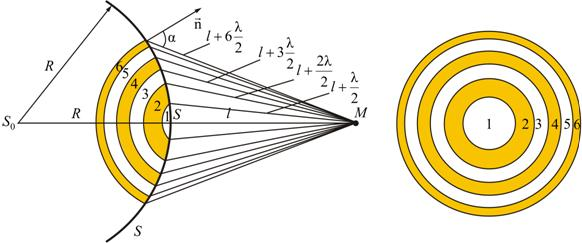
Рис. 9.2

      Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга:

      где A – амплитуда результирующего колебания,   – амплитуда колебаний, возбуждаемая i-й зоной Френеля.

      Величина   зависит от площади   зоны и угла  между нормалью к поверхности и прямой, направленной в точку M.

      Площадь одной зоны

.

      Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.

      В то же время с увеличением номера зоны возрастает угол  и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда . Она уменьшается также из-за увеличения расстояния до точки M:

 .

      Общее число зон Френеля, умещающихся на части сферы, обращенной в сторону точки M, очень велико: при , , число зон , а радиус первой зоны .

      Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.

      Световая волна распространяется прямолинейно. Фазы колебаний, возбуждаемые соседними зонами, отличаются на π. Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания  от некоторой m-й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.

.

      Тогда выражение (9.2.1) можно записать в виде

.

(9.2.2)

      Так как площади соседних зон одинаковы, то выражения в скобках равны нулю, значит результирующая амплитуда .

      Интенсивность излучения   .

      Таким образом, результирующая амплитуда, создаваемая в некоторой точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной, а интенсивность .

      Так как радиус центральной зоны мал следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно.

      Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке M будет равна . Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к. ). Интенсивность света увеличивается, если закрыть все четные зоны.

      Таким образом, принцип Гюйгенса–Френеля позволяет объяснить прямолинейное распространение света в однородной среде.

      Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонные пластинки – система чередующихся прозрачных и непрозрачных колец.

      Опыт подтверждает, что с помощью зонных пластинок можно увеличить освещенность в точке М, подобно собирающей линзе.