Гипотеза де-Бройля. Волновые свойства вещества

Недостаточность теории Бора сделала необходимым критический пересмотр основ квантовой теории и представлений о природе элементарных частиц (электронов, протонов и т. п,). Возник вопрос о том, насколько исчерпывающим является представление электрона в виде малой механической частицы, характеризуемой определенными координатами и определенной скоростью.

В результате углубления наших знаний о природе света выяснилось, что в оптических явлениях обнаруживается своеобразный дуализм (см. § 57). Наряду с такими свойствами света, которые самым непосредственным образом свидетельствуют о его волновой природе (интерференция, дифракция), имеются и другие свойства, столь же непосредственно обнаруживающие его корпускулярную природу (фотоэффект, явление Комп-тона).

В 1924 г. Луи де-Бройль выдвинул смелую гипотезу, что дуалн-зм не является особенностью одних только оптических явлений, но имеет универсальное значение. «В оптике, — писал он, — в течение столетия слишком пренебрегали корпускулярным способом рассмотрения по сравнению с волновым; не делалась ли в теории вещества обратная ошибка?»

Допуская, что частицы вещества наряду с корпускулярными свойствами имеют также и волновые, де-Бройль перенес на случай частиц вещества те же правила пе-

рехода от одной картины к другой, какие справедливы в случае света. Фотон, как известно [см. формулы (57.1) и (57.4)], обладает энергией

и импульсом

По идее де-Бройля, движение электрона или какой-либо другой частицы связано с волновым процессом, длина волны которого равна

а частота

Гипотеза де-Бройля вскоре была блестяще подтверждена экспериментально. Дэвиссон и Джермер обнаружили, что пучок электронов, рассеивающийся от кристаллической пластинки, дает дифракционную картину. Томсон и независимо от него Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу. Опыт осуществлялся следующим образом (рис. 190). Пучок электронов, ускоренных разностью потенциалов порядка нескольких десятков киловольт, проходил через тонкую металлическую фольгу и попадал на фотопластинку. Электрон при ударе о фотопластинку оказывает на нее такое же действие, как и фотон. Полученная таким способом электронограмма золота (рис. 191, а) сопоставлена с полученной в аналогичных условиях рентгенограммой алюминия (рис. 191,6). Сходство обеих картин поразительно.

Штерн и его сотрудники показали, что дифракционные явления обнаруживаются также у атомных и молекулярных пучков. Во всех перечисленных случаях

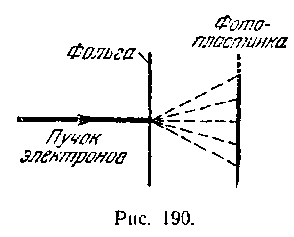
дифракционная картина соответствует длине волны, определяемой соотношением (64.1).

Из описанных опытов с несомненностью вытекает, что пучок микрочастиц определенной скорости и

■аправлеиия дает дифракционную картину, подобную картине, получаемой от плоской волны.

Дифракция электронов — процесс рассеяния электронов на совокупности частиц вещества, при котором электрон проявляет волновые свойства. Данное явление называется корпускулярно-волновым дуализмом, в том смысле, что частица вещества(в данном случае взаимодействующие электроны) может быть описана, как волна.

ДИФРАКЦИЯ НЕЙТРОНОВ - явление рассеяния нейтронов, в к-ром определяющую роль играют волновые свойства нейтрона (см. Корпускулярно-волновой дуализм ).Длина волны  и импульс р связаны соотношением де Бройля  =hp. Матем. описание Д. н., так же как и в случае др. волновых полей, следует из принципа Гюйгенса - Френеля и, в этом смысле, аналогично описаниюдифракции света, рентг. лучей, электронов и др. микрочастиц (см. Дифракция волн ).Согласно этому описанию, интенсивность рассеянного излучения в некрой точке пространства зависит как от  , так и от свойств рассеивающего объекта. Соответственно, Д. н. применяется как для исследования или формирования нейтронных пучков (нейтронные монохроматоры, анализаторы), так и для исследований строения рассеивающего вещества.

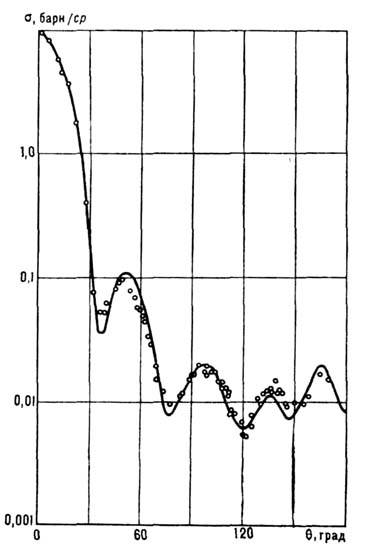
Рис. 1. Угловое распределение нейтронов с энергией 14 МэВ, рассеянных на ядре Sn;  - сечение рассеяния;   - угол рассеяния.

Оценка энергии нулевых колебаний осциллятора. Будем действовать точно так же, как и в предыдущем примере. Энергия классического одномерного гармонического осциллятора описывается выражением

E = px2 / 2m + mω2x2 / 2.

Рассматривая px и х как неопределенности импульса и координаты осциллирующего микрообъекта и пользуясь в качестве соотношения неопределенностей равенством pxх = h, получаем

Е(px) = px2 / 2m + mω2h2 / 2px2 .

Приравнивая к нулю производную , находим величину

р0 = mωh, при которой функция Е(px) принимает минимальное значение. Легко убедится, что это значение равно

Е = Е(p0) = hω.

Этот результат весьма интересен. Он показывает, что в квантовой механике энергия осциллятора не может обратиться в нуль; ее минимальное значение оказывается порядка hω. Это есть так называемая энергия нулевых колебаний.

Учитывая существование нулевых колебаний, можно прийти, в частности, к следующему интересному заключению: энергия колебательного движения атомов кристалла не обращается в не обращается в нуль даже при температуре абсолютного нуля.

Нулевые колебания иллюстрируют принципиальное общее обстоятельство: нельзя реализовать микрообъект на «дне потенциальной ямы», или, иначе говоря, «микрообъект не может упасть на дно потенциальной ямы». Этот вывод не зависит от вида потенциальной ямы, так как является прямым следствием соотношений неопределенности импульса; в этом случае неопределенность координаты должна стать сколь угодно большой, что противоречит самому факту пребывания микрообъекта в потенциальной яме.

Туннелирование электрона через потенциальный барьер является принципиально квантово-механическим эффектом, который не имеет аналога в классической механике. Туннельный эффект является экспериментальным подтверждением одного из фундаментальных исходных положений квантовой механики - корпускулярно-волнового дуализма свойств элементарных частиц.

Туннельным эффектом называется возможность элементарной частице, например электрону, пройти (протуннелировать) через потенциальный барьер, когда барьер выше полной энергии частицы. Возможность существования туннельного эффекта в микромире была понята физиками в период создания квантовой механики, в 20-30-х годах нашего века. В дальнейшем за счет туннельного эффекта были объяснены некоторые весьма важные явления, обнаруженные экспериментально в различных областях физики.