5.3. Потери на трение в трубопроводах. Опыты Никурадзе. График вти

Потери на трение при турбулентном режиме определяются по формуле:

.

(5.3)

Наиболее сложным является определение коэффициента . В общем случае коэффициент  зависит от критерия Re, величины шеро­ховатости стенок и характера шероховатости:

,

(5.4)

где  – средняя величина неровности стенок;

– относительная шероховатость;

A – параметр, учитывающий характер шероховатости.

Первые опыты по исследованию зависимости  от Re и для напорных трубопроводов с искусственной шероховатостью проведены в Геттингенском университете (1930 –1933 г.г.) Никурадзе.

Никурадзе определял величину коэффициента сопротивления по длине при движении различных жидкостей по трубам разного диаметра при разных относительных шероховатостях, полученных путём наклейки на стенки трубы однородных песчинок, и разных Re. Песчинки получали просеиванием песка через сита. Испытания были произведены при широком диапазоне относительных шерохова­тостей , а также Re = 500  10⁶. Результаты этих испытаний представлены на логарифмическом графике Ig100 от lgRe для ряда значений (рис. 5.5).

Рис. 5.5

Особый интерес представляет анализ графика Никурадзе. В графике можно выделить следующие характерные зоны: I зона – здесь  = f(Re). Это зона ламинарного режима движения жидкости и, как известно, коэффициент  зависит только от числа Re

.

(5.5)

II зона. Это зона гидравлически гладких труб. Она прости­рается при 4000  Re  20 . Как указывалось выше, такое "поведение" труб имеет место в силу того, что ламинарный подслой перекры­вает выступы шероховатости ( > ). Вихри, образующиеся на выступах шероховатости, гаснут в ламинарном слое и не попадают в турбулентное ядро.

III зона. Здесь . Пределы этой зоны определяются соотношением

.

(5.6)

IV зона. Здесь  = f ( ) и не зависит от Rе. Она но­сит название квадратичной. В этой зоне ламинарный подслой нас­только мал, что все выступы шероховатости оказываются в турбу­лентном ядре и именно это оказывает влияние на величину коэф­фициента .

Сопротивление труб с естественной шероховатостью отличает­ся от сопротивления труб с искусственной шероховатостью.

Н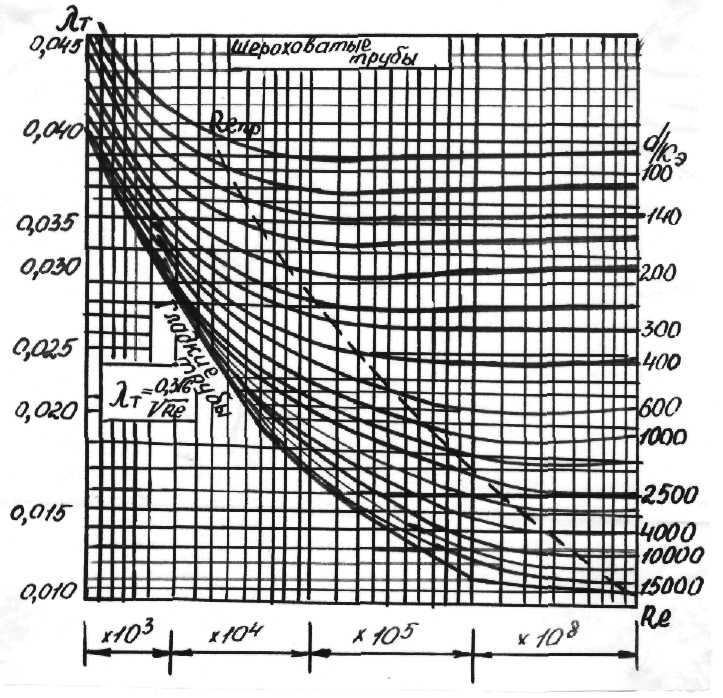 а рис. 5.6 приведён график, полученный во Всесоюзном теп­лотехническом институте для труб с естественной шероховатостью. Для натуральных труб закон изменения  от Rе получается несколь­ко иным, без подъёма кривых после отклонения их от закона для гладких труб.

Рис. 5.6

Коэффициент  на графике дан в зависимости от Rе для раз­ных значений , где к_э – абсолютная шероховатость, эквивалент­ная* зернистой шероховатости в опытах Никурадзе.

* Эквивалентная шероховатость - это такая высота выступов песчинок в опытах Никурадзе, которая создаёт сопротивление, рав­ное действительному сопротивлению данного трубопровода. Значения к_э находят в гидравлических справочниках.

Такой постепенный переход объясняют тем, что в случае разнозернистой шероховатости: при увеличении Re, а следова­тельно, уменьшении толщины вязкого подслоя _л выступы шеро­ховатости вступают в соприкосновение с турбулентным потоком не все одновременно, а сначала наиболее высокие, затем средние и только при числах Re, соответствующих квадратичной области сопротивления, вязкий подслой освобождает все выступы шерохо­ватости,