Аппроксимация статистических рядов и проверка гипотез

О выборе закона распределения.

Под аппроксимацией статистических рядов будем понимать выбор вида закона распределения и значений его параметров по имеющимся экспериментальным данным.

При статистической оценке неизвестных параметров распределения, мы исходим из того, что вид закона распределения с.в. был известен из каких-либо теоретических соображений, либо его нахождение не являлось необходимым. Требовалось лишь знание значений параметров этого закона.

Однако, во многих случаях, сам вид закона распределения является гипотетическим и нуждается в статистической проверке на достоверность.

Процедура выбора вида закона распределения в большинстве случаев не поддаётся строгой формализации. Главную роль здесь играют интуиция и опыт исследователя, и априорные сведения о характере исследуемой с.в. или явления.

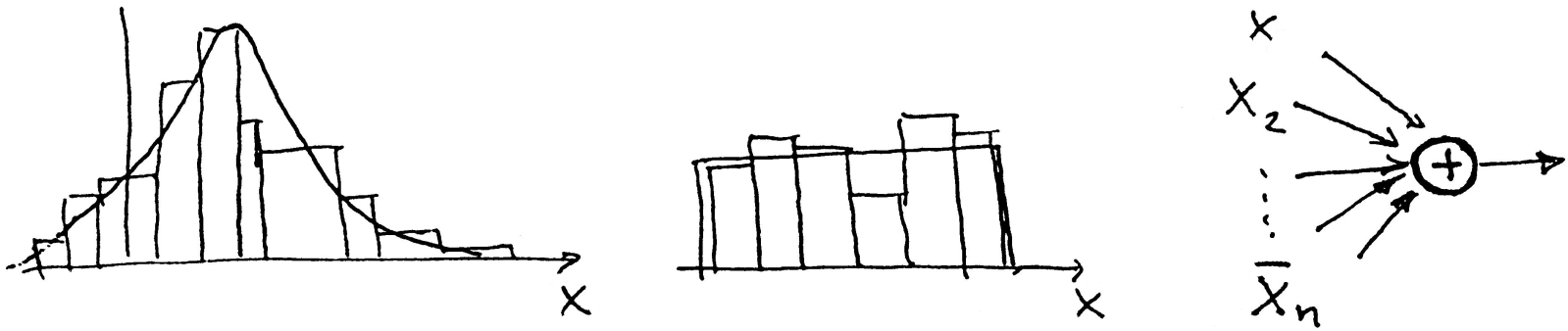
Кроме того, в зависимости от вида, закон распределения имеет различное число параметров:

• Нормальный закон распределения – 2 (m_x , σ_x)

• Биномиальный закон распределения – 2 (p , n)

• Равномерный закон распределения – 2 (a , b)

• Закон распределения Пуассона – 1 (а)

В результате анализа физической природы С.В. может быть выдвинута гипотеза о законе её распределения, которая по результатам многократных наблюдений над С.В. может быть принята или отвергнута.

Рассмотрим задачу о статистической проверке гипотезы о законе распределения С.В. с помощью критериев согласия. Под статистической гипотезой будем понимать всякое предположение о законе распределения и его параметрах, сделанное на основании наблюдений над С.В.

Критерии согласия

Пусть Х – С.В., относительно которой выдвинута гипотеза Н₀ о том, что она подчинена некоторому закону распределения F(x).

Для проверки гипотезы произведём выборку объёма n, состоящую из независимых наблюдений с.в. Х: х₁ , х₂ , … , х_n.

Необходимо определить – согласуются ли данные наблюдения с принятым в гипотезе H₀ законом распределения F(x).

С этой целью по результатам случайной выборки х₁ , х₂ , … , х_n строится статистическая функция распределения F*(x).

Вводится некоторая неотрицательная мера U, которая характеризует величину отклонения статистической функции распределения F*(x) от предполагаемой теоретической F(x). Эта мера может быть определена различными способами, зависит от результатов наблюдений и является случайной величиной U = U(F_n*(x), F(x)) .

Закон распределения меры U в общем случае зависит от закона распределения с.в. X и объёма выборки n.

Однако, в ряде случаев удаётся найти такой её вид, что закон её распределения при больших n не зависит от F(x).

Критерий согласия  - Колмогорова.

Пусть Х – непрерывная с.в., для которой получены результаты n опытов.

Считаем, что n достаточно велико, и экспериментальные данные позволяют выдвинуть гипотезу о законе распределения и построить статистическую функцию распределения F*(x).

Проверке подвергается гипотеза о том, что Х имеет функцию распределения F(x).

В качестве меры рассогласования между теоретическим и статистическим распределениями берётся максимальное значение модуля разности между статистической функцией F*(x) и теоретической функцией распределения F(x).

Колмогоров доказал, что какова бы ни была функция распределения F(x) непрерывной с.в. Х, при n→∞ случайная величина , всегда имеет один и тот же закон распределения,

который затабулирован (распределение -Колмогорова). Функция распределения -Колмогорова приведена ниже. Очевидно, что чем больше , тем меньше согласование экспериментального и теоретического распределения.