
- •1. Понятие функции одной независимой переменной. Способы задания функции. Функции заданные аналитически. Область определения, область изменения функции.
- •2. Определения: предела функции при х-х0; х-беск геометрическая иллюстрация
- •3. Бесконечно малые функции при х-х0; х-беск определения, геометрич иллюстраци. Св-ва бесконечно малых.
- •Свойства бесконечно малых
- •4.Беск большие функции при х-х0; х-беск определения, геометр иллюстрация. Связь между бесконечно большой и малой функциями.
- •5. Теорема о разности между функцией и ее пределом. Теорема о пределе суммы, произведения и частного функций.
- •6.Сравнение бесконечно малых функций. Эквивалентные бесконечно малые, их свойства.
- •7.Приращение аргумента и приращение функции, их геометрическая иллюстрация. Два равносильных определения функции, непрерывной в точке. Непрерывность основных элементарных функций.
- •[Править]Комментарии
- •Элементарные функции
- •8. Теорема о непрерывности суммы, произведения и частного функции.
- •11. Производные суммы, произведения и частного функций. Производная сложной функции.
- •12. Теорема о непрерывности функции имеющую производную в точке (доказательство)
- •13. Определение дифференциала функции, его связь с приращением функции, форма, геометрический смысл, применение к приближенным вычислениям.
- •14. Теорема Ферма, Ролля, Лагранжа, их геометрический смысл. (доказательство)
- •15. Определение функции монотонно возрастающей (убывающей) на интервале. Достаточный признак монотонного возрастания (убывания) функции на интервале. (доказательство)
- •16. Определение точки максимума (минимума) функции. Необходимый признак экстремума (доказательство).
- •17. Первый достаточный признак экстремума (доказательство). Второй достаточный признак экстремума (формулировка).
- •10.5. Достаточный признак экстремума
- •18. Определение выпуклости вверх (вниз) графика функции на интервале. Достаточный признак выпуклости вверх (вниз). (доказательство).
- •19. Определение точки перегиба. Необходимы признак точки перегиба. Достаточный признак точки перегиба (доказательство).
16. Определение точки максимума (минимума) функции. Необходимый признак экстремума (доказательство).
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Пусть функция
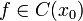 непрерывна
в
непрерывна
в 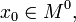 и
существуют конечные или бесконечные
односторонние производные
и
существуют конечные или бесконечные
односторонние производные 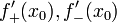 .
Тогда при условии
.
Тогда при условии
![]()
является точкой строгого локального максимума. А если
![]()
то является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке
Пусть функция непрерывна и дважды дифференцируема в точке . Тогда при условии
![]() и
и ![]()
является точкой локального максимума. А если
и ![]()
то является точкой локального минимума.
Пусть функция дифференцируема
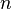 раз
в точке
и
раз
в точке
и 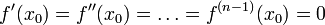 ,
а
,
а 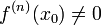 .
.
Если
чётно
и ![]() ,
то
-
точка локального максимума. Если
чётно
и
,
то
-
точка локального максимума. Если
чётно
и ![]() ,
то
-
точка локального минимума. Если
нечётно,
то экстремума нет.
,
то
-
точка локального минимума. Если
нечётно,
то экстремума нет.
17. Первый достаточный признак экстремума (доказательство). Второй достаточный признак экстремума (формулировка).
10.5. Достаточный признак экстремума
использующий вторую производную. Наименьшее
и наибольшее значения функции на отрезке
Т:
(достаточный признак э. II) Пусть![]() а
а![]() суще-
суще-
ствует
и непрерывна в некоторой окрестности
т.![]() Если
Если ![]() то
функция имеет max в т.
то
функция имеет max в т.![]() если
если![]() то
функция имеет min в т.
то
функция имеет min в т.![]() Пусть
Пусть![]() В
силу непрерывности
В
силу непрерывности![]() сохраняет
знак всюду в окрестности т.
сохраняет
знак всюду в окрестности т.![]() по
достаточному признаку монотонности
по
достаточному признаку монотонности![]() в
окрестности т.
в
окрестности т.![]() но
но![]()
при![]() при
при![]() (рис.
10.8). По достаточному признаку э. I в
т.
(рис.
10.8). По достаточному признаку э. I в
т.![]() функция
имеет max.
функция
имеет max.
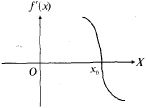
Рис. 10.8
Аналогичные рассуждения для случая
![]()
Достаточный
признак э. II применим только для
случая![]() т.е.
для стационарных точек
т.е.
для стационарных точек![]()
Пример:![]()
![]()
Применим
сведения об экстремумах для нахождения
наибольшего и наименьшего значений
функции![]() на
отрезке [a, b].
на
отрезке [a, b].
Пусть![]() и
дифференцируема на (а, b) за исключени-
и
дифференцируема на (а, b) за исключени-
ем, быть может, конечного числа точек. Она достигает своего наименьшего и наибольшего значений (свойство 1° непрерывных на [а, b] функций), которые могут находиться или в точках экстремума, или на концах отрезка.
Таким
образом, чтобы найти наибольшее и
наименьшее значения![]() на
[а, b], необходимо:
на
[а, b], необходимо:
1) найти точки на [а, b], подозрительные на экстремум;
2) найти значения функции в этих точках и на концах промежутка [а, b], выбрать из них наименьшее и наибольшее значения.
Пример:![]()
1)![]() при
при![]()
2)![]()
18. Определение выпуклости вверх (вниз) графика функции на интервале. Достаточный признак выпуклости вверх (вниз). (доказательство).
Определение 1. График функции y=f(x) называется выпуклым (вогнутым) на интервале (a,b), если касательная к графику, проведенная в любой точке этого интервала, расположена над (под) графиком функции.
|
|
|
|
Выпуклый график, Вогнутый график,
![]() <0.
>0.
<0.
>0.
Теорема 1. Если вторая производная дважды дифференцируемой функции на некотором интервале отрицательна (положительна), то график функции на данном интервале выпуклый (вогнутый).
Верна и обратная теорема.
Определение 2. Точки, в которой график функции меняет направление выпуклости, называют точками перегиба графика функции.
Y

y=f(x)
0 a c X
Точка a является точкой перегиба, а точка c нет, так как в этой точке функция не дифференцируема.
Теорема
2. (необходимый
признак точки перегиба). Если
точка х0 является
точкой перегиба графика дважды
дифференцируемой функции, то в этой
точке вторая производная равна нулю: ![]() =0.
=0.
Определение 3. Точки, в которых вторая производная равна нулю или не существует, называются критическими точками второй производной. Если функция имеет точки перегиба, то они могут быть только в критических точках.
Теорема 3 (достаточный признак точки перегиба). Если вторая производная дважды дифференцируемой функции в некоторой точке равна нулю и при переходе через нее вторая производная меняет знак, то данная точка является точкой перегиба.

