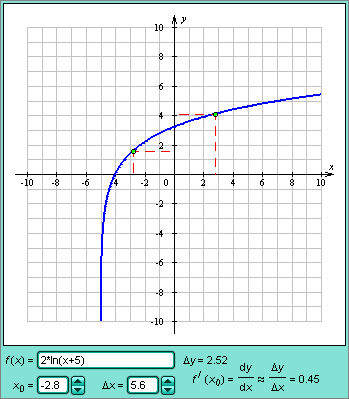
- •1. Понятие функции одной независимой переменной. Способы задания функции. Функции заданные аналитически. Область определения, область изменения функции.
- •2. Определения: предела функции при х-х0; х-беск геометрическая иллюстрация
- •3. Бесконечно малые функции при х-х0; х-беск определения, геометрич иллюстраци. Св-ва бесконечно малых.
- •Свойства бесконечно малых
- •4.Беск большие функции при х-х0; х-беск определения, геометр иллюстрация. Связь между бесконечно большой и малой функциями.
- •5. Теорема о разности между функцией и ее пределом. Теорема о пределе суммы, произведения и частного функций.
- •6.Сравнение бесконечно малых функций. Эквивалентные бесконечно малые, их свойства.
- •7.Приращение аргумента и приращение функции, их геометрическая иллюстрация. Два равносильных определения функции, непрерывной в точке. Непрерывность основных элементарных функций.
- •[Править]Комментарии
- •Элементарные функции
- •8. Теорема о непрерывности суммы, произведения и частного функции.
- •11. Производные суммы, произведения и частного функций. Производная сложной функции.
- •12. Теорема о непрерывности функции имеющую производную в точке (доказательство)
- •13. Определение дифференциала функции, его связь с приращением функции, форма, геометрический смысл, применение к приближенным вычислениям.
- •14. Теорема Ферма, Ролля, Лагранжа, их геометрический смысл. (доказательство)
- •15. Определение функции монотонно возрастающей (убывающей) на интервале. Достаточный признак монотонного возрастания (убывания) функции на интервале. (доказательство)
- •16. Определение точки максимума (минимума) функции. Необходимый признак экстремума (доказательство).
- •17. Первый достаточный признак экстремума (доказательство). Второй достаточный признак экстремума (формулировка).
- •10.5. Достаточный признак экстремума
- •18. Определение выпуклости вверх (вниз) графика функции на интервале. Достаточный признак выпуклости вверх (вниз). (доказательство).
- •19. Определение точки перегиба. Необходимы признак точки перегиба. Достаточный признак точки перегиба (доказательство).
11. Производные суммы, произведения и частного функций. Производная сложной функции.
12. Теорема о непрерывности функции имеющую производную в точке (доказательство)
13. Определение дифференциала функции, его связь с приращением функции, форма, геометрический смысл, применение к приближенным вычислениям.
Итак,
график дифференцируемой функции в
окрестности каждой своей точки сколь
угодно близко приближается к графику
касательной в силу равенства: ![]() где
α – бесконечно малая в окрестности
где
α – бесконечно малая в окрестности ![]() функция.
Для приближенного вычисления значения
функции f в
точке x0 + Δx эту
бесконечно малую функцию можно отбросить:
функция.
Для приближенного вычисления значения
функции f в
точке x0 + Δx эту
бесконечно малую функцию можно отбросить:
|
Линейную
функцию ![]() называют дифференциалом
функции f в
точке
и
обозначают df.
Для функции x производная
в каждой точке
равна 1,
то есть
называют дифференциалом
функции f в
точке
и
обозначают df.
Для функции x производная
в каждой точке
равна 1,
то есть ![]() Поэтому
пишут:
Поэтому
пишут:
|
Приближенное значение функции вблизи точки равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом:
|
Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется функция.
|
Модель 3.3. Дифференциал функции. |
Геометрически дифференциал функции df – это приращение ординаты касательной к графику функции в данной точке при изменении абсциссы точки на dx.
14. Теорема Ферма, Ролля, Лагранжа, их геометрический смысл. (доказательство)
еорема Ферма. Если функция у = f (х), определенная в интервале (а ; b), достигает в некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует производная f ′(с), то f ′(с) = 0.
Геометрический
смысл этой теоремы состоит в том, что
касательная к графику функции у = f (х)
в точке с абсциссой с параллельна
оси абсцисс (рис.).
 Теорема
Ролля. Если
функция у = f (х),
непрерывная на отрезке [а ; b]
и дифференцируемая в интервале
(а ; b),
принимает на концах этого отрезка равные
значения f (a)
= f (b),
то в интервале (а ; b)
существует такая точка с,
что f ′(с)
= 0.
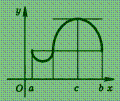
Геометрически
эта теорема означает следующее: если
крайние ординаты кривой у = f (х)
равны, то на кривой найдется точка, в
которой касательная параллельна оси
абсцисс (рис.).
Теорема
Ролля. Если
функция у = f (х),
непрерывная на отрезке [а ; b]
и дифференцируемая в интервале
(а ; b),
принимает на концах этого отрезка равные
значения f (a)
= f (b),
то в интервале (а ; b)
существует такая точка с,
что f ′(с)
= 0.
Геометрически
эта теорема означает следующее: если
крайние ординаты кривой у = f (х)
равны, то на кривой найдется точка, в
которой касательная параллельна оси
абсцисс (рис.).
 Теорема
Лагранжа. Если
функция у = f (х)
непрерывна на отрезке [а ; b]
и дифференцируема в интервале
(а ; b),
то в этом интервале найдется такая
точка с,
что
Теорема
Лагранжа. Если
функция у = f (х)
непрерывна на отрезке [а ; b]
и дифференцируема в интервале
(а ; b),
то в этом интервале найдется такая
точка с,
что ![]()
Эта
теорема имеет простой геометрический
смысл (рис.): на графике функции у = f (х)
между точками А и В найдется
такая внутренняя точка С,
что касательная к графику в
точке С параллельна
хорде АВ. 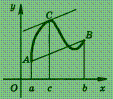
Следствие. Если f ′(x) = 0 в интервале (а ; b), то в этом интервале функция f (х) постоянна.
15. Определение функции монотонно возрастающей (убывающей) на интервале. Достаточный признак монотонного возрастания (убывания) функции на интервале. (доказательство)
Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.
Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
Пусть
дана функция ![]() Тогда
Тогда
функция называется возраста́ющей на
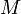 ,
если
,
если
![]() .
.
функция называется стро́го возраста́ющей на , если
![]() .
.
функция называется убыва́ющей на , если
![]() .
.
функция называется стро́го убыва́ющей на , если
![]() .
.
Монотонная функция, определённая на интервале, измерима относительно борелевских сигма-алгебр.
Монотонная функция,
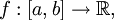 определённая
на замкнутом интервале, ограничена.
В частности, она интегрируема
по Лебегу.
определённая
на замкнутом интервале, ограничена.
В частности, она интегрируема
по Лебегу.Монотонная функция может иметь разрывы только первого рода. В частности, множество точек разрыва не более чем счётно.
Монотонная функция
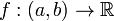 дифференцируема почти
всюду относительно меры
Лебега.
дифференцируема почти
всюду относительно меры
Лебега.