
- •1. Понятие функции одной независимой переменной. Способы задания функции. Функции заданные аналитически. Область определения, область изменения функции.
- •2. Определения: предела функции при х-х0; х-беск геометрическая иллюстрация
- •3. Бесконечно малые функции при х-х0; х-беск определения, геометрич иллюстраци. Св-ва бесконечно малых.
- •Свойства бесконечно малых
- •4.Беск большие функции при х-х0; х-беск определения, геометр иллюстрация. Связь между бесконечно большой и малой функциями.
- •5. Теорема о разности между функцией и ее пределом. Теорема о пределе суммы, произведения и частного функций.
- •6.Сравнение бесконечно малых функций. Эквивалентные бесконечно малые, их свойства.
- •7.Приращение аргумента и приращение функции, их геометрическая иллюстрация. Два равносильных определения функции, непрерывной в точке. Непрерывность основных элементарных функций.
- •[Править]Комментарии
- •Элементарные функции
- •8. Теорема о непрерывности суммы, произведения и частного функции.
- •11. Производные суммы, произведения и частного функций. Производная сложной функции.
- •12. Теорема о непрерывности функции имеющую производную в точке (доказательство)
- •13. Определение дифференциала функции, его связь с приращением функции, форма, геометрический смысл, применение к приближенным вычислениям.
- •14. Теорема Ферма, Ролля, Лагранжа, их геометрический смысл. (доказательство)
- •15. Определение функции монотонно возрастающей (убывающей) на интервале. Достаточный признак монотонного возрастания (убывания) функции на интервале. (доказательство)
- •16. Определение точки максимума (минимума) функции. Необходимый признак экстремума (доказательство).
- •17. Первый достаточный признак экстремума (доказательство). Второй достаточный признак экстремума (формулировка).
- •10.5. Достаточный признак экстремума
- •18. Определение выпуклости вверх (вниз) графика функции на интервале. Достаточный признак выпуклости вверх (вниз). (доказательство).
- •19. Определение точки перегиба. Необходимы признак точки перегиба. Достаточный признак точки перегиба (доказательство).
4.Беск большие функции при х-х0; х-беск определения, геометр иллюстрация. Связь между бесконечно большой и малой функциями.
Бесконечно большая величина
Во
всех приведённых ниже формулах
бесконечность справа от равенства
подразумевается определённого знака
(либо «плюс», либо «минус»). То есть,
например, функция ![]() ,
неограниченная с обеих сторон, не
является бесконечно большой при
,
неограниченная с обеих сторон, не
является бесконечно большой при ![]() .
.
Последовательность
называется бесконечно
большой,
если ![]() .
.
Функция
называется бесконечно
большой в окрестности точки
,
если ![]() .
.
Функция
называется бесконечно
большой на бесконечности,
если ![]() либо
либо ![]() .
.
Теорема 1 (о связи предела с бесконечно малой функцией). Для того, чтобы существовал
|
f(x) = A, |
|
необходимо и достаточно, чтобы функцию f(x) можно было представить в виде
|
f(x) = A + α(x), |
|
где α(x) — бесконечно малая функция при x → x0.
Связь между бесконечно малыми и бесконечно большими функциями
Если f(x) — бесконечно большая функция при x → x0, то
1
f(x)
— бесконечно малая функция при x → x0.
Если α(x) — бесконечно малая функция при x → x0 и x
·
O
(x0) α(x) ≠ 0, то
1
α(x)
— бесконечно большая функция при x → x0.
5. Теорема о разности между функцией и ее пределом. Теорема о пределе суммы, произведения и частного функций.
ТЕОРЕМА 1. Предел суммы двух функций при x стремящемся к a равен сумме пределов этих функций ТЕОРЕМА 2. Предел произведения двух функций при x стремящемся к a равен произведению пределов этих функций ТЕОРЕМА 3. Предел частного двух функций при x стремящемся к a равен частному пределов, если предел знаменателя отличен от нуля
6.Сравнение бесконечно малых функций. Эквивалентные бесконечно малые, их свойства.
Определения
Допустим,
у нас есть бесконечно малые при одном
и том же ![]() величины
величины ![]() и
и ![]() (либо,
что не важно для определения, бесконечно
малые последовательности).
(либо,
что не важно для определения, бесконечно
малые последовательности).
Если
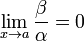 ,
то
,
то 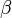 —
бесконечно малая высшего
порядка малости,
чем
—
бесконечно малая высшего
порядка малости,
чем 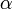 .
Обозначают
.
Обозначают 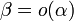 .
.Если
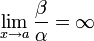 ,
то
—
бесконечно малая низшего
порядка малости,
чем
.
Соответственно
,
то
—
бесконечно малая низшего
порядка малости,
чем
.
Соответственно 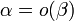 .
.Если
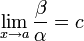 (предел
конечен и не равен 0), то
и
являются
бесконечно малыми величинами одного
порядка малости.
(предел
конечен и не равен 0), то
и
являются
бесконечно малыми величинами одного
порядка малости.
Это
обозначается как ![]() или
или ![]() (в
силу симметричности данного отношения).
(в
силу симметричности данного отношения).
Если
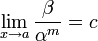 (предел
конечен и не равен 0), то бесконечно
малая величина
имеет
(предел
конечен и не равен 0), то бесконечно
малая величина
имеет 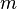 -й
порядок малости относительно
бесконечно малой
.
-й
порядок малости относительно
бесконечно малой
.
Для вычисления подобных пределов удобно использовать правило Лопиталя.
[править]Примеры сравнения
При
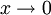 величина
величина 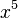 имеет
высший порядок малости относительно
имеет
высший порядок малости относительно 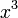 ,
так как
,
так как 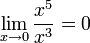 .
С другой стороны,
имеет
низший порядок малости относительно
,
так как
.
С другой стороны,
имеет
низший порядок малости относительно
,
так как 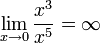 .
.
С
использованием О-символики полученные
результаты могут быть записаны в
следующем виде ![]() .
.
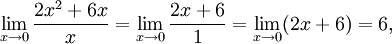 то
есть при
то
есть при 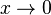 функции
функции 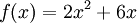 и
и 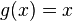 являются
бесконечно малыми величинами одного
порядка.
являются
бесконечно малыми величинами одного
порядка.
В
данном случае справедливы записи ![]() и
и ![]()
При бесконечно малая величина
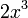 имеет
третий порядок малости относительно
имеет
третий порядок малости относительно 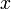 ,
поскольку
,
поскольку 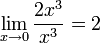 ,
бесконечно малая
,
бесконечно малая 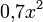 —
второй порядок, бесконечно малая
—
второй порядок, бесконечно малая 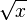 —
порядок 0,5.
—
порядок 0,5.
Определение
Если ![]() ,
то бесконечно малые
величины
и
называются эквивалентными (
,
то бесконечно малые
величины
и
называются эквивалентными (![]() ).
).
Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.
При ![]() справедливы
следующие соотношения эквивалентности
(как следствия из так называемых замечательных
пределов):
справедливы
следующие соотношения эквивалентности
(как следствия из так называемых замечательных
пределов):
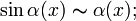
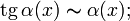
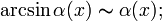
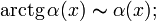
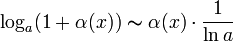 ,
где
,
где 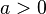 ;
;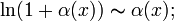
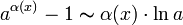 ,
где
;
,
где
;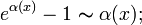

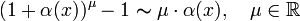 ,
поэтому используют выражение:
,
поэтому используют выражение:
![]() ,
где
.
,
где
.
