Юстировка и исследование макета компенсатора нивелира "Ni-007"

Принцип работы компенсатора можно пояснить на макете установки для исследования стабильности линии визирования нивелира (рис. 2).

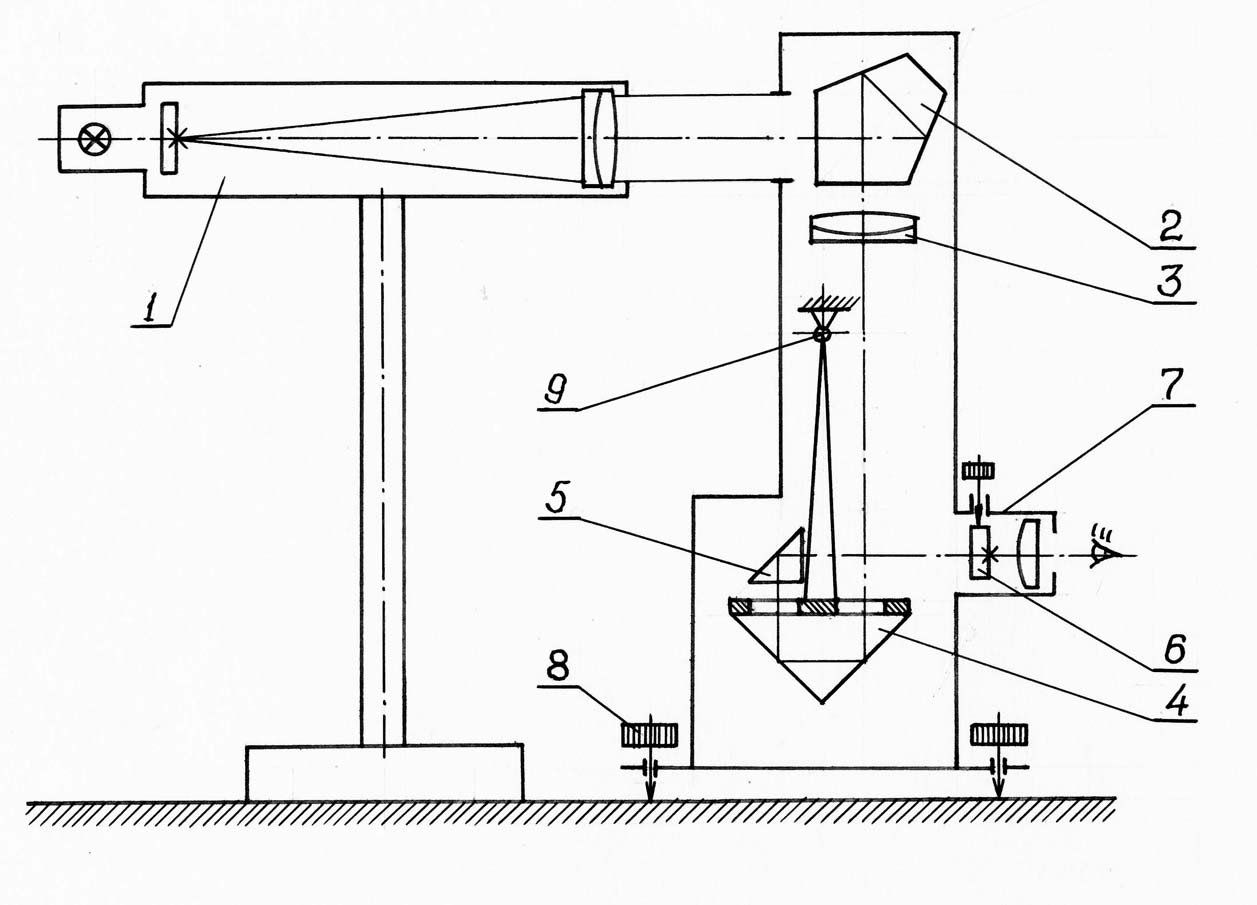
Рис. 2. Схема установки для исследования компенсатора

Пучок световых лучей из коллиматора 1, имитирующего линию горизонта, падает на пентапризму 2 нивелира перископического типа, попадает в объектив 3, проходит призму 4 типа БР-180° компенсатора, неподвижную призму 5 типа АР-90°, и строит изображение горизонтальной линии на сетке 6 окулярного микрометра 7.

Призма 4 компенсатора, свободно подвешенная с помощью рычага на оси качания 9, осуществляет сдвиг изображения сетки нивелира.

При наклоне макета нивелира на угол  изображение горизонтальной нити сетки коллиматора сместится на величину f ', призма – на величину S, а изображение сетки, наблюдаемое со стороны объектива нивелира, - на 2S, где f ' – фокусное расстояние объектива, S- расстояние от точки подвеса рычага до ребра призмы (длина рычага).

Из уравнения (1) находим коэффициент компенсации

f '/ S = k = 2. (2)

При выполнении этого требования линия горизонта, создаваемая коллиматором 1, будет совпадать с горизонтальным штрихом сетки нивелира, что исключит погрешность измерений из-за наклона нивелира.

При юстировке макета необходимо получить резкое изображение горизонтального штриха сетки коллиматора 1 и с помощью маховичка окулярного микрометра 7 привести его в биссектор сетки 6, а также отрегулировать длину плеча рычага для выполнения равенства (2).

Юстировка осуществляется смещением и разворотом узла сетки с окуляром нивелира (в качестве такого узла использован стандартный окуляр-микрометр). Длина плеча рычага регулируется специальным устройством.

Исследование компенсатора заключается в анализе влияния первичных погрешностей компенсатора и определении пределов его работы. Наклоняя основание макета передним установочным винтом 8 последовательно на углы 1; 12; 36; 1 вниз и затем вверх от горизонта, измеряют уход линии горизонта, создаваемого коллиматором 1, от биштриха сетки 6. Величина угла наклона основания макета нивелира определяется долями или целым числом оборотов переднего установочного винта 8 , имеющего шаг резьбы t=0,75 мм и действующего на длине плеча рычага R=205 мм. Как нетрудно подсчитать - цена одного оборота винта 8 при этих параметрах составит, примерно, 12' (угл.мин.).

Технические подробности [1-5].

Вывод выражения для определения величины корректирующего изменения длины рычага для выполнения условия компенсации

Как было показано выше, условие компенсации можно представить следующим выражением:

, (3)

где - «длина рычага», а точнее - расстояние от точки подвеса призмы компенсатора до ребра эквивалентного прямоугольного углового зеркала, которому эквивалентна стеклянная призма БР-180°.

Это выражение получается из условия компенсации смещения сетки нивелира по отношению к объективу (при наклоне прибора) сдвигом изображения этой сетки, осуществляемым призмой - компенсатором, подвешенной с помощью рычага на оси качания подобно маятнику.

Пусть для исходного положения прибора неизвестная нам длина рычага равна (начальная), которую можно представить как

. (4)

Здесь - значение длины рычага, при котором происходит точная компенсация направления линии визирования при наклоне прибора, - искомое нами корректирующее изменение длины рычага, позволяющее добиться условия компенсации (3). Снимем начальный отсчёт по окулярному микрометру. Далее наклоним прибор на угол и снимем следующий отсчёт по окулярному микрометру. Составим первое уравнение

. (5)

Изменим длину рычага на и снимем отсчёт по окулярному микрометру. Составим второе уравнение

. (6)

Ещё раз изменим длину рычага, и это суммарное его изменение по отношению к обозначим как . Снова снимем отсчёт по окулярному микрометру - , и напишем третье уравнение: