3.Игры против природы. Рандомизированные решения

Рандомизированным решением ЛПР называется распределение вероятностей на множестве его обычных решений:

, ,

Критериями оптимальности для р.-решений служат те же критерии, что и рассмотренные выше критерии для обычных, нерандомизированных решений. Отличие лишь только в том, что при этом между собой сравниваются значения средних выигрышей (потерь), вычисляемые по формуле

(3)

где – вероятность свершения состояния природы.

Поиск оптимальных р.-решений по критерию Лапласа. Применяется при отсутствии какой-либо информации о вероятностях свершения состояний природы. Оптимальное по критерию Лапласа р.-решение находится из решения следующей задачи линейного программирования:

, (4)

,

Значения являющиеся компонентами оптимального плана задачи (4), и определяют искомое оптимальное р.-решение по критерию Лапласа.

Поиск оптимальных р.-решений по критерию ожидаемого значения (Байеса). Применяется, когда известны вероятности свершения всех состояний природы. Оптимальное р.-решение находится из решения задачи линейного программирования

, (5)

,

Значения являющиеся компонентами оптимального плана задачи (5), и определяют искомое оптимальное р.-решение по критерию ожидаемого значения (Байеса) при заданных вероятностях состояний природы.

Пример 4. В условиях примера 1 находим оптимальное р.-решение по критерию Байеса для заданных априорных вероятностей свершения состояний природы: . Следуя (5), для заданных значений элементов матрицы полезностей получаем задачу:

,

Полученную задачу линейного программирования решаем с помощью надстройки «Поиск решения» (рис. 4). В ответе получаем решение , означающее, что всю продукцию следует подвергнуть решению . Ожидаемое значение прибыли при этом равно 11,13.

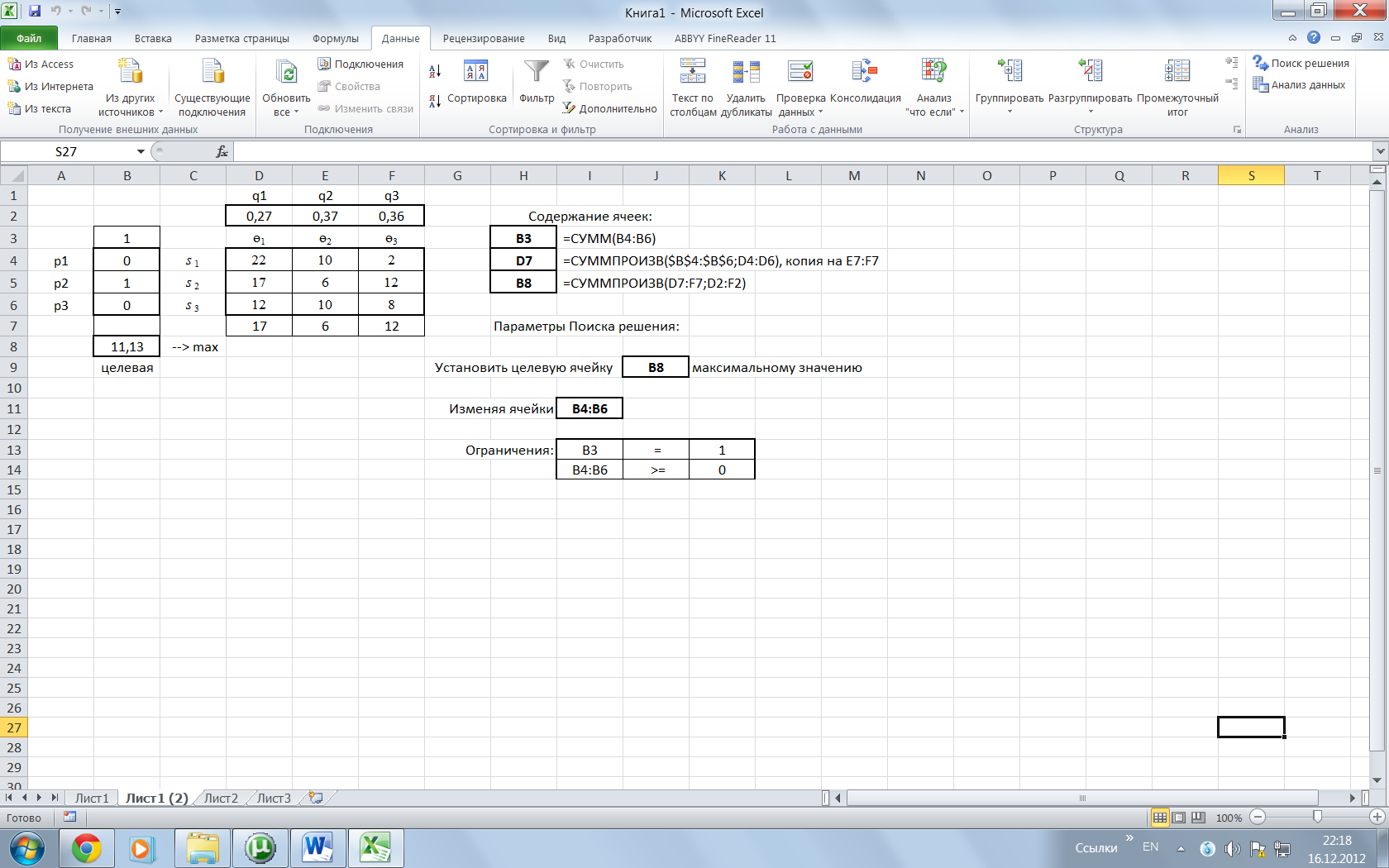
Рис. 4. Шаблон с решением задачи примера 4

Поиск оптимальных р.-решений по критерию гарантированного результата (максимину и минимаксу). Данные критерии применяются тогда, когда необходимо получить гарантированный результат. В зависимости от того, является ли матрица исходов матрицей полезности или матрицей потерь, применяется либо критерий максимина (задача максимизации), либо критерий минимакса (задача минимизации). К ответу ведут решения следующих задач линейного программирования:

критерий максимина: (для матрицы полезности):	критерий минимакса: (для матрицы потерь):
(6);	(7)

Пример 5. В условиях примера 1 находим оптимальное р.-решение по критерию максимина. Следуя (6), для заданных значений элементов матрицы полезностей получаем задачу:

Полученную задачу линейного программирования решаем с помощью надстройки «Поиск решения» (рис. 5).

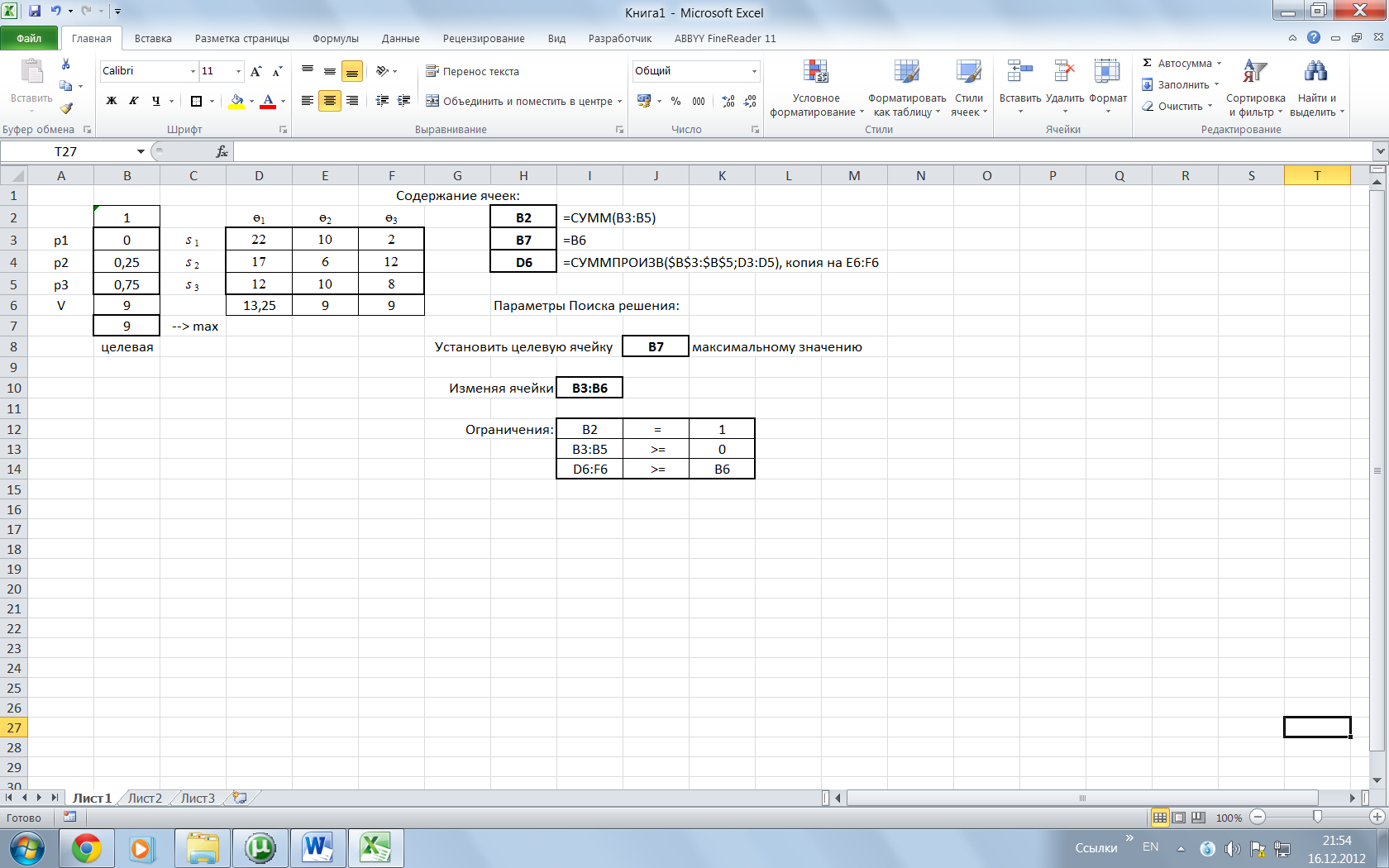
Рис. 5. Шаблон с решением задачи примера 5

В ответе получаем решение , означающее, что четверть всей продукции следует подвергнуть решению , а три четверти – решению . Гарантированное среднее значение прибыли при этом равно 9.

Поиск оптимальных р.-решений по критерию Неймана-Пирсона. Критерий Неймана-Пирсона применяется тогда, когда природа может иметь всего два состояния, одно из которых находится под контролем. Пусть задана некоторая пороговая величина , и все р.-решения ЛПР, при которых его средние потери превышают порог (выигрыши меньше порога), отвергаются как недопустимые. Из всех допустимых р.-решений оптимальным по критерию Неймана-Пирсона объявляется то, при котором средние потери при неконтролируемом состоянии минимальны (выигрыш максимален). В зависимости от того, является ли матрица исходов матрицей полезности или матрицей потерь, получаем следующие задачи:

(для матрицы полезности):	(для матрицы потерь):
область индексов допустимых решений; и потери ЛПР при контролируемом и неконтролируемом состояниях соответственно.	область индексов допустимых решений; и потери ЛПР при контролируемом и неконтролируемом состояниях соответственно.

Задачи для самостоятельного решения

Задача 3. Предприятие выпускает скоропортящуюся продукцию, которую может направить на продажу сразу (решение А₁ ), отправить на склад для хранения (решение А₂ ) или подвергнуть дополнительной обработке (решение А₃) для длительного хранения. Характер спроса на продукцию "Весны" определяется состоянием рынка; при этом предполагается, что возможны три состояния: продукция "Весны" приобретается немедленно (состояние В₁), в течение небольшого периода времени (состояние В₂), после длительного периода времени (состояние В₃ ). В случае решений А₂ и А₃ предприятие несет дополнительные затраты на хранение и обработку продукции, которые не требуются при А₁, однако при А₁ следует учесть возможные убытки из-за порчи продукции, если состояние рынка будет В₂ или В₃. Матрица прибылей предприятия «Весна» задана:

	В1	В2	В3
A1	22	10	2
A2	17	6	12
A3	12	10	8

Найти оптимальное нерандомизированное решение предприятия по критериям Лапласа и Байеса при условии, что вероятности состояний В₁, В₂ и В₃ равны соответственно 0,3, 0,3 и 0,4.

Ответ: оптимальным решением как по критерию Лапласа, так и по критерию Байеса является A₂.

Задача 4. В условиях задачи 3 найти оптимальное решение по критерию Сэвиджа.

Ответ: оптимальным решением по критерию Сэвиджа является решение A₂.

Задача 5. В условиях задачи 3 найти оптимальные нерандомизированные решения по критерию Гурвица для ЛПР с показателями оптимизма .

Ответ: оптимальными нерандомизированными решениями по критерию Гурвица являются:

для показателя оптимизма – решение A₁;

для показателя оптимизма – решение A₁;

для показателя оптимизма – решение A₃;

Задача 6. В условиях задачи 3 найти оптимальное рандомизированное решение по критерию максимина (т.е., оптимальные пропорции применения решений А₁, А₂, А₃ , дающие гарантированный средний уровень прибылей).

Ответ: . Гарантированная средняя прибыль при этом равна .

Задача 7. Магазин может завезти в различных пропорциях товары трех типов ; их реализация и прибыль магазина зависят от вида товара и состояния спроса. Предполагается, что спрос может иметь три состояния и не прогнозируется. Определить оптимальные пропорции в завозе товаров из условия максимизации средней гарантированной прибыли при следующей матрице прибылей:

Тип товара	Спрос
	В1	В2	В3
А1	20	15	10
А2	16	12	14
А3	13	18	15

Ответ: . Гарантированная средняя прибыль при этом равна .

Задача 8. Ежедневный спрос в кулинарии на пирожные стоимостью 49 руб. задается следующим распределением вероятностей ( кол-во булочек, вероятность):

D	100	150	200	250	300
p(D)	0,20	0,25	0,30	0,15	0,10

Себестоимость одного пирожного составляют 25 руб. Если пирожное не продано в течение дня, оно реализуется за 15 рублей. Используя критерий Байеса, определите, какое оптимальное число пирожных нужно изготовлять ежедневно, если предположить, что величина заказа может принимать одно из возможных значений спроса.

Ответ: оптимальное количество пирожных – 200 шт. Оптимальная ожидаемая прибыль при этом составит 3695 руб.