3. Задачи для самостоятельного решения

Задача 3.1. Мелкооптовый продавец может закупить несколько контейнеров огурцов, для их последующей распродажи в течение недели более мелкими партиями – ящиками. Розничной торговлей он не занимается. В каждом контейнере находится 100 ящиков с овощами. Общие издержки, связанные с приобретением, перевозкой, хранением и т.д. одного контейнера, составляют 70000 руб.; начальная продажная цена ящика со свежими овощами – 900 руб. Если в течение недели все огурцы не удается продать, то в самом конце недели оптовик реализует их остаток по сниженной цене – 300 руб. за ящик. Используя критерий ожидаемого значения (Байеса), определите, сколько контейнеров следует приобрести оптовику, чтобы получить максимум ожидаемой прибыли за недельный цикл, при условии, что вероятности спроса (количество ящиков с овощами, приобретаемых у оптовика в неделю по начальной цене) заданы в таблице:

Количество ящиков
100	200	300	400	500	600	700	800	900	1000
0,05	0,05	0,1	0,1	0,2	0,2	0,1	0,1	0,05	0,05
Вероятности спроса

Чему равна максимальная ожидаемая прибыль за недельный цикл?

Ответ: следует приобрести 5 контейнеров. Максимальная ожидаемая прибыль за недельный цикл равна 61000 руб.

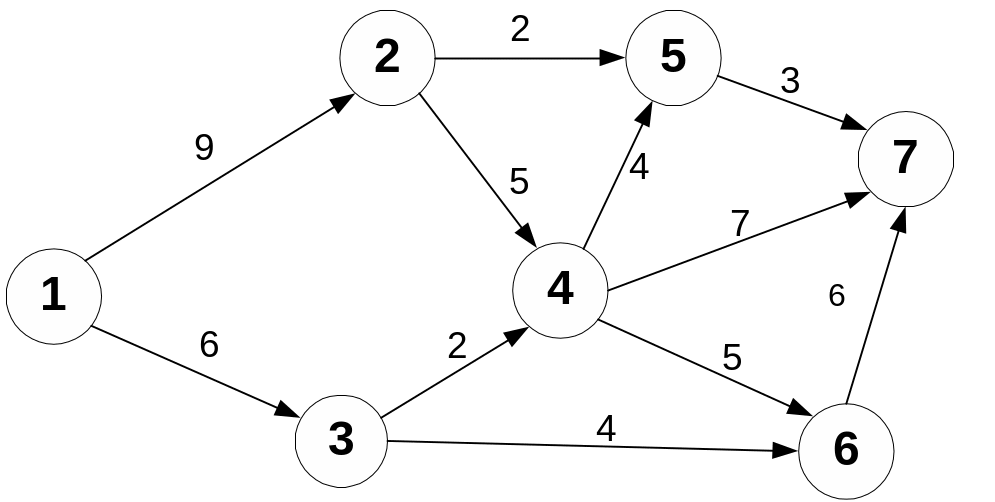
Задача 3.2. Дорожная сеть состоит из семи транспортных узлов, соединенных между собой дорогами. Передвижение между узлами возможно лишь в одном направлении (движение однонаправленное); разрешенные направления движения обозначены стрелками. Числа, стоящие у стрелок, означают расстояние между узлами (км). Необходимо найти кратчайший и критический (самый длинный) пути проезда из узла 1 в узел 7.

Ответ: искомый кратчайший путь проходит через узлы 1-2-5-7. Его длина равна 14 км. Критический путь проходит через узлы 1-2-4-6-7. Его длина равна 25 км.

Задача 3.3. Дорожная сеть состоит из двенадцати транспортных узлов, соединенных между собой дорогами (рис. 3.1). Разрешенные направления движения обозначены стрелками. Числа, стоящие у стрелок, означают расстояние между узлами (км). Необходимо найти наикратчайший путь проезда из узла 1 в узел 12.

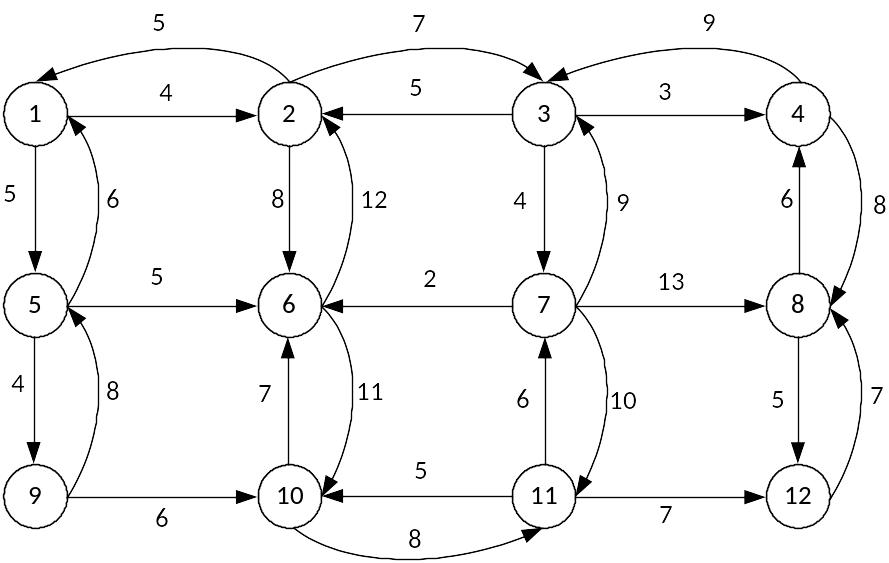
Рис. 3.1. Дорожная сеть

Ответ: кратчайший путь проходит через узлы 1-2-3-4-8-12. Его длина равна 27 км.

Задача 3.4. Для дорожной сети рис 3.1 найти кратчайшие пути проезда из пункта 12 в пункт 1 и из пункта 9 в пункт 4.

Ответ: кратчайший путь из пункта 12 в пункт 1 проходит через узлы 12-8-4-3-2-1; длина равна 32 км. Кратчайший путь из пункта 9 в пункт 4 проходит через узлы 9-5-1-2-3-4; длина равна 28 км.

Задача 3.5. Решить задачу 3.4 при условии, что пятый пункт закрыт для движения.

Ответ: кратчайший путь из пункта 12 в пункт 1 проходит через узлы 12-8-4-3-2-1; длина равна 32 км. Кратчайший путь из пункта 9 в пункт 4 проходит через узлы 9-10-11-7-3-4; длина равна 32 км.

Задача 3.6. Для дорожной сети на рис 3.2 найти кратчайший и критический пути проезда из пункта 1 в пункт 6.

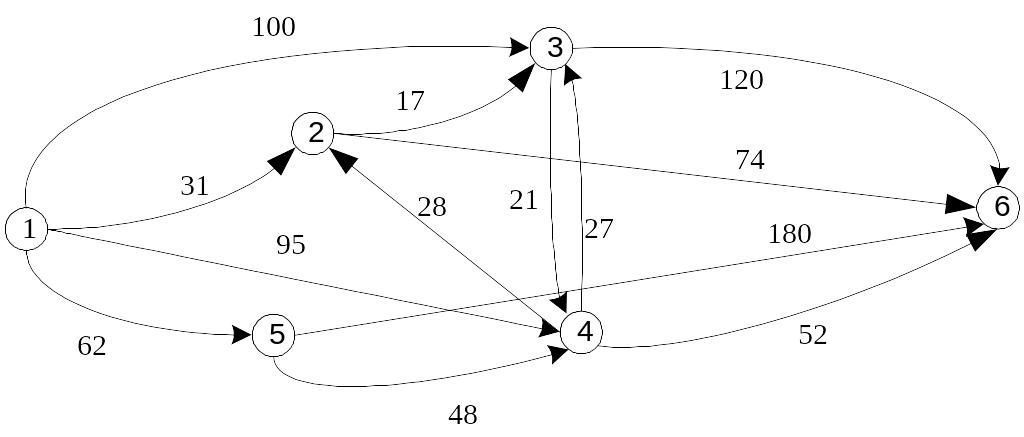
Рис. 3.2. Дорожная сеть

Ответ: кратчайший путь проходит через узлы 1-2-6; длина равна 105 км. Критический путь проходит через узлы 1-5-4-2-3-6; длина равна 323 км.

Задача 3.7. Дорожная сеть (рис. 3.3) состоит из девяти транспортных узлов, соединенных между собой дорогами. Пропускные характеристики каждой из дорог (в тыс. автомобилей в час) в направлениях, указанных стрелками, заданы. Числа, стоящие рядом со стрелками, означают максимально возможную пропускную способность соответствующих дорожных участков в указанных направлениях. Требуется определить максимальную пропускную способность данной дорожной сети в целом, то есть, определить, какое максимальное число автомобилей может проехать за 1 час из начального узла 1 сети в ее конечный узел 9.

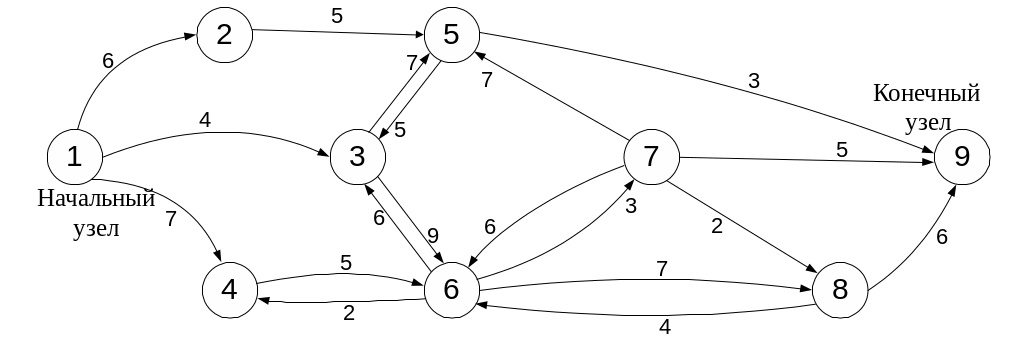
Рис. 3.3. Дорожная сеть

Ответ: максимальное значение для входного потока в контрольный 9-й узел сети – 12 тыс. автомобилей в час.

Задача 3.8. Сеть нефтепроводов состоит из девяти узлов, соединенных между собой трубами (рис. 3.4). Перекачка нефти между узлами возможна лишь в направлениях, указанных стрелками. Рядом с каждой из стрелок проставлены два числа, из которых одно заключено в скобки. То из чисел, которое не заключено в скобки, означает пропускную способность соответствующей трубы (у.е.). Число, заключенное в скобки, означает стоимость единицы потока по данной трубе (у.е.). Требуется найти распределение потоков по сети минимальной суммарной стоимости при условии, что суммарный приток в 9-й узел должен быть не менее 90 у.е.

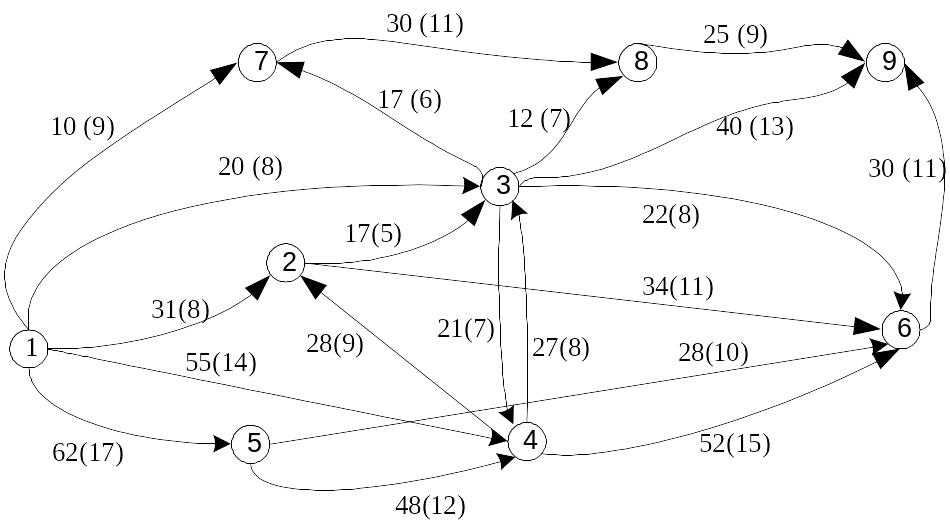
Рис. 3.4. Сеть нефтепроводов

Задача 3.9. Для сети на рис. 3.4 рассчитать ее максимальную пропускную способность между 1-м и 9-м узлами без учета стоимости потоков.

Задача 3.10. Решить задачу 3.8 при условии, что третий узел выведен из строя и прокачка нефти через него невозможна.

Задача 3.11. Решить задачу 3.8 при условии, что четвертый узел выведен из строя и прокачка нефти через него невозможна.