Занятие 5
1.Сетевые задачи
1.1. Задачи, связянные с определением кратчайшего и критического путей
Словесная
формулировка. Необходимо найти
кратчайший или самый протяженный
(критический) путь между заданными
исходной и конечной вершинами (узлами,
пунктами) сети
и
.
Формальная
постановка. Пусть задана сеть с графом
и матрицей инцидентности
;
при этом каждой дуге
сопоставлено число
,
означающее длину этой дуги. Введем в
рассмотрение переменные
,
значения которых определяются следующим
образом:
,
если дуга
присутствует в пути;
в противном случае.
Тогда задача о кратчайшем (критическом) пути предстает в виде задачи линейного дискретного программирования:
(1.1.1)
(1.1.2)
Ограничения
(1.1.2) являются необходимыми условиями,
при которых набор дуг, соответствующих
ненулевым значениям
,
образует путь, соединяющий
и
.
1.2. Задачи, связянные с определением оптимальных потоков в сети
Задача о
максимальном потоке. Словесная
формулировка. Необходимо рассчитать
величины потоков по дугам графа сети,
которые бы обеспечивали максимальный
приток в узел-приемник
.
При этом величина данного притока должна
быть равна величине истока из узла-источника
,
а величины потоков по всем дугам сети
не должны превышать их пропускные
способности, заданные числами. Суммарный
приток по каждому узлу сети (за исключением
приемника и источника) при этом должен
быть равен суммарному истоку из этого
узла (для исключения скоплений и дефицита
потока).
Формальная
постановка. Рассмотрим сеть с графом
,
матрица инцидентности
которого задана. Предположим, что каждой
дуге
сопоставлено число
,
означающее «пропускную способность»
этой дуги (у.е.). Обозначим через
,
величину потока по дуге
.
Тогда задача о максимальном потоке
принимает вид
(1.2.1)
(1.2.2)
Здесь
суммарный
втекающий в узел-приемник
поток. Первое ограничение в системе
ограничений (1.2.2) означает равенство
вытекающего из
и втекающего в
потоков. Второе ограничение означает
условие исключения скоплений и дефицита
потока для любого промежуточного узла
сети. Третье ограничение в (1.2.2) означает
условие того, что потоки по дугам не
могут превысить заданные предельно
допустимые значения (пропускные
способности дуг).
Задача о потоке минимальной стоимости. Словесная формулировка. Нужно рассчитать величины потоков минимальной суммарной стоимости по дугам сети, которые бы обеспечивали заданный суммарный приток в узел-приемник .
Формальная
постановка. Пусть задана сеть с графом
,
и матрицей инцидентности
.
Предположим, что каждой дуге
сопоставлены числа
и
,
означающие «пропускную способность»
этой дуги и стоимость единицы потока
соответственно (у.е.). Пусть величина
притока в узле-приемнике должна быть
не меньше некоторой заданной величины
.
Обозначим через
величину потока по дуге
.
Тогда задача о потоке минимальной
стоимости сводится к следующей задаче
линейного программирования:
(1.2.3)
(1.2.4)
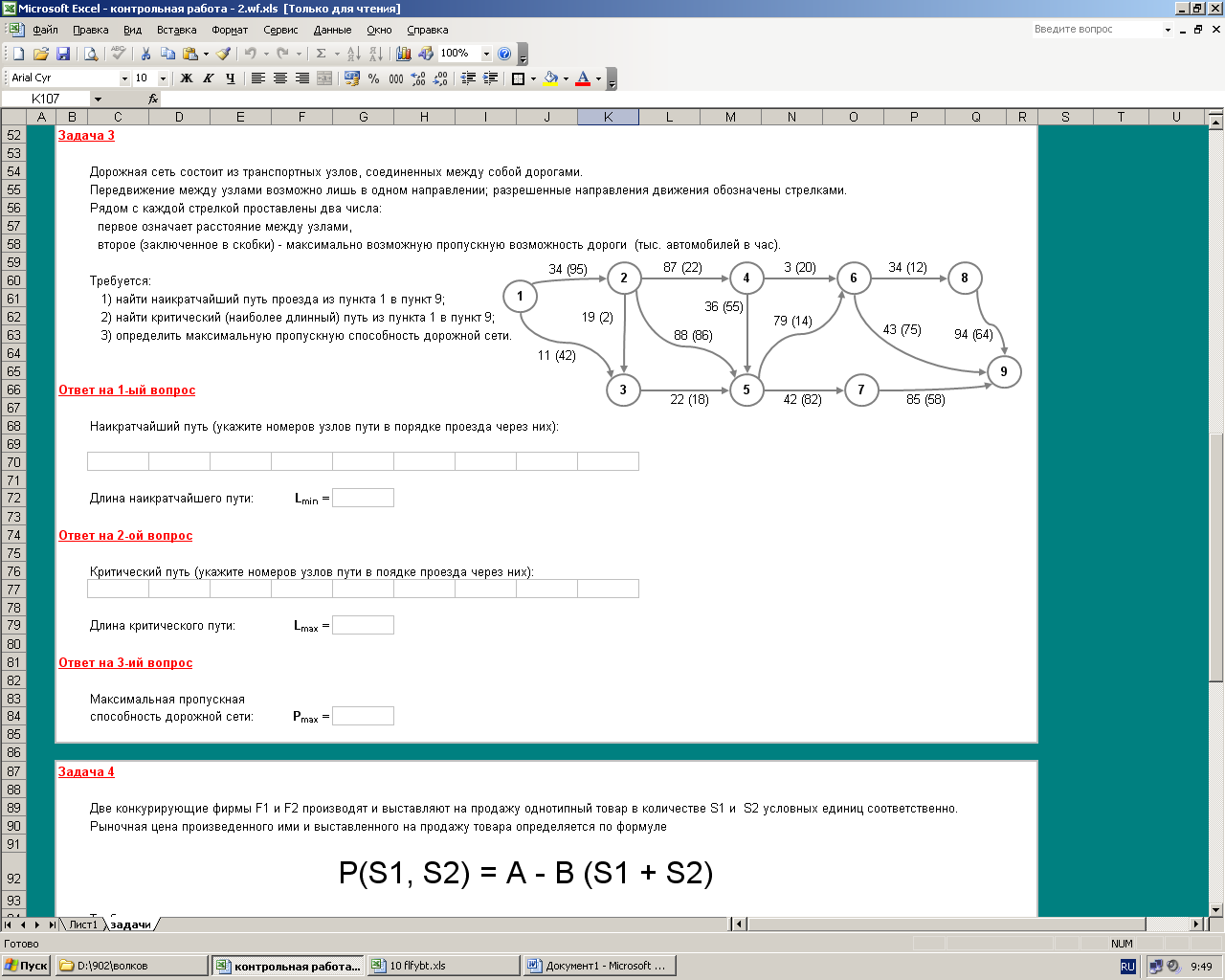
Задача 1.1. Дорожная сеть состоит из транспортных узлов, соединенных между собой дорогами. Передвижение между узлами возможно лишь в одном направлении, разрешенные направления движения обозначены стрелками. Рядом с каждой стрелкой проставлены два числа: первое означает расстояние между узлами; второе (заключенное в скобки) – максимально возможную пропускную способность дороги (тыс.автомобилей в час).
Требуется:
1) найти наикратчайший путь проезда из пункта 1 в пункт 9; 2) найти критический (наиболее длинный) путь из пункта 1 в пункт 9; 3) определить максимальную пропускную способность дорожной сети |
|
Решение. Ответы на первый и второй вопросы находим, следуя (1.1.1)-(1.1.2). Реализуем следующие действия:
1) Из рисунка на рабочий лист вводим информацию по всем дугам сети (ячейки A35:D48 на шаблоне, рис.1.1 ниже);
2) перечисляем номера всех узлов сети (ячейки E34:M34);
3) вычисляем элементы матрицы инцидентности (ячейки E35:M48);
4) отводим столбец N35:N48 («выбор пути») под ячейки, которые будут определять искомый путь;
5) вычисляем итоги взаимодействия входящих в путь дуг со всеми узлами сети (ячейки E49:M49);
6) вычисляем суммарную длину всех дуг, образующих искомый путь (ячейка C49);
7) заносим в ячейки E50:M50 значения, определяющих сценарий пути (для начального узла пути заносим –1, для конечного узла заносим 1, для всех остальных заносим 0);
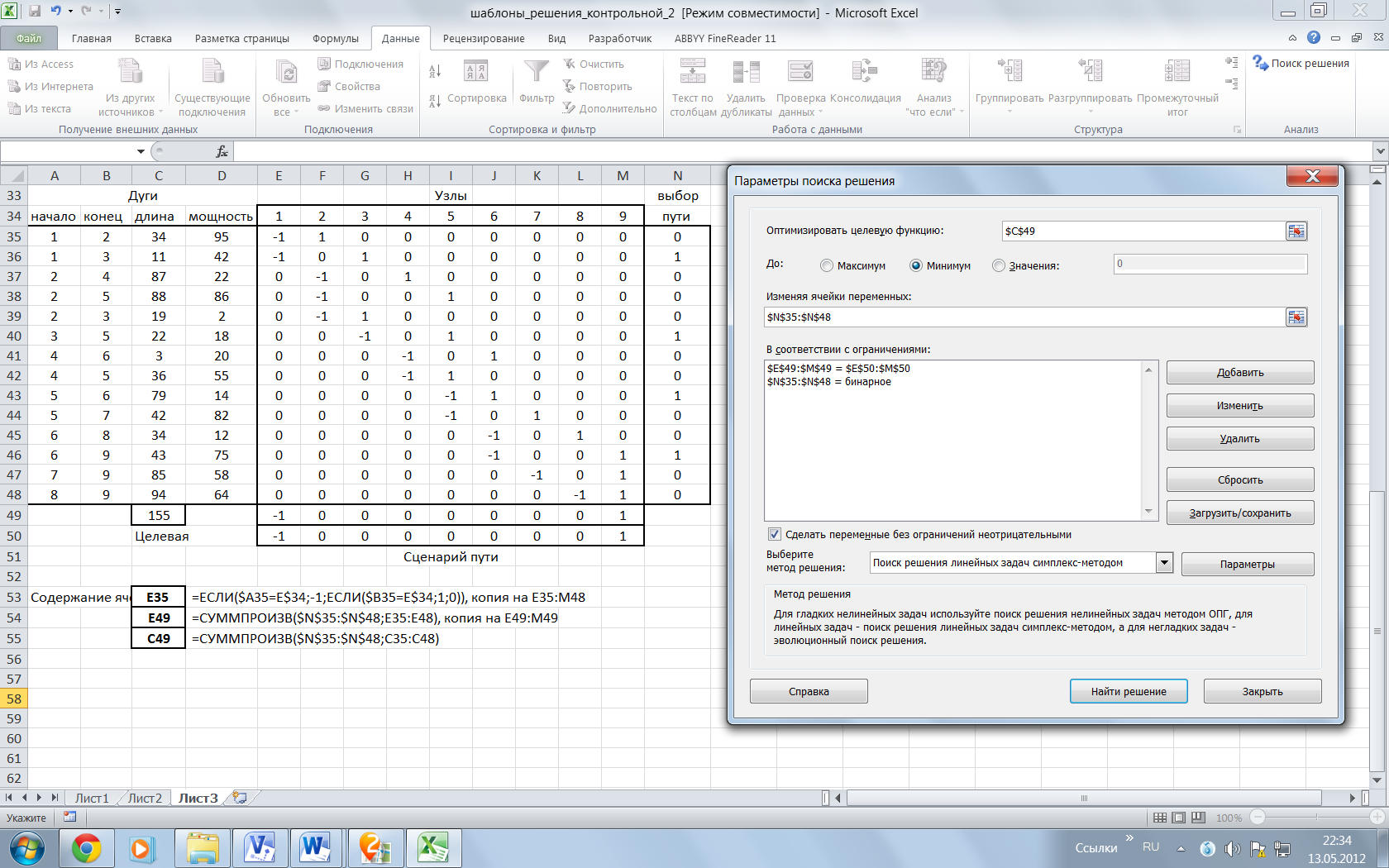
8) ставим задачу в «Поиске решения», отмечая при этом линейную модель, и решаем ее (рис.1.1):
|
Параметры Поиска решения:
Установить целевую ячейку С49 минимальному значению
Изменяя ячейки N35:N48
Ограничения:
Е49:М49 = Е50:М50 N35:N48 двоичное |
Рис.1.1. Шаблон с решением задачи 1.1 для ответа на первый вопрос
Для получения ответа на второй вопрос делаем копию листа рис. 1.1; вызываем «Поиск решения», целевую ячейку устанавливаем на максимальное значение; даем команду «выполнить» и получаем ответ на второй вопрос.
Для получения ответа на третий вопрос необходимо решить задачу по определению максимальной пропускной способности. Следуя (1.2.2)-(1.2.3), делаем следующие шаги:
1) копируем лист (рис. 1.1), где решалась задача определения пути минимальной длины;
2) на скопированном листе удаляем строку со сценарием пути и ячейку с длиной пути (рис. 1.2);
3) заголовок «выбор пути» над столбцом N35:N28 изменяем на заголовок «потоки» (рис. 1.2);
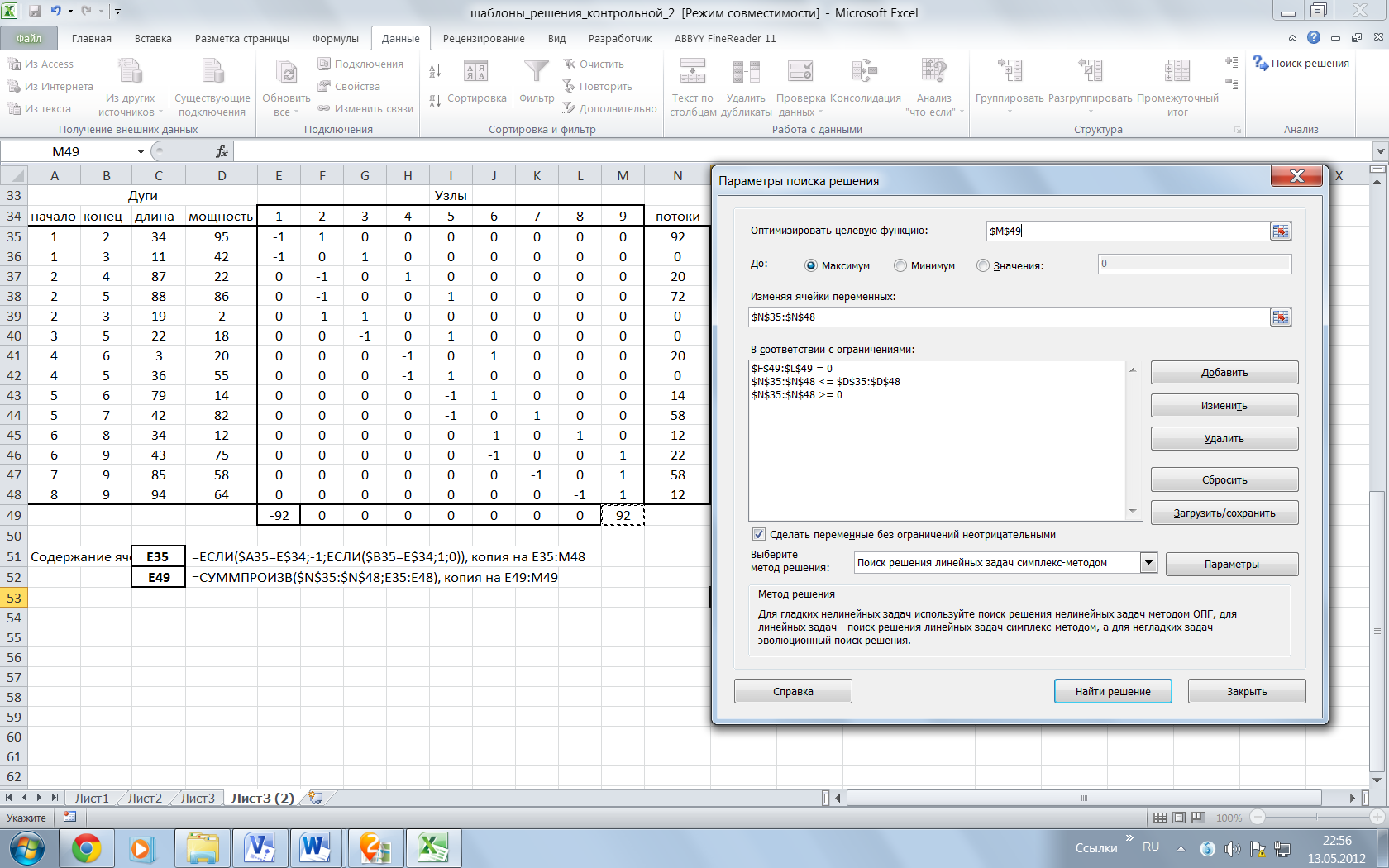
4) ставим задачу в «Поиске решения» и решаем ее (рис. 1.2):
|
Параметры Поиска решения:
Установить целевую ячейку М49 максимальному значению
Изменяя ячейки N35:N48
Ограничения:
F49:L49 = 0 N35:N48>=0 N35:N48 <= D35:D48 |
Рис. 1.2. Шаблон с решением задачи 1.1 для ответа на третий вопрос